Solving Absolute Value Inequalities
In this lesson, we are going to learn how to solve absolute value inequalities using the standard approach usually taught in an algebra class. That is, learn the rules and apply them correctly. There are four cases involved when solving absolute value inequalities.
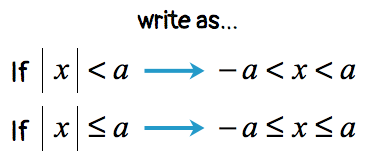
CAUTION: In all cases, the assumption is that the value of “[latex]a[/latex]” is positive, that is, [latex]a > 0[/latex].
Four (4) Cases to Consider When Solving Absolute Value Inequalities
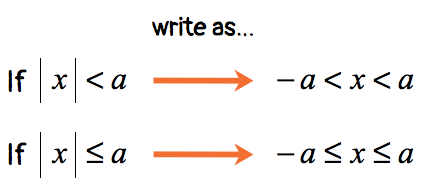
CASE 1:
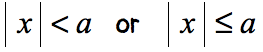
CASE 2:
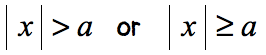
CASE 3:
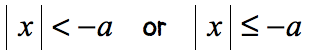
The absolute value of any number is either zero [latex](0)[/latex] or positive which can never be less than or equal to a negative number.
The answer to this case is always no solution.
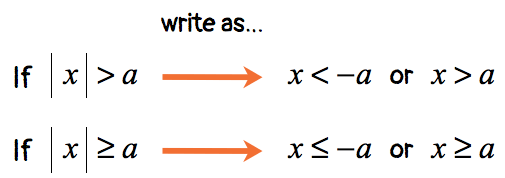
CASE 4:
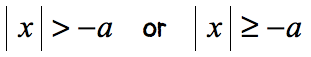
The absolute value of any number is either zero [latex](0)[/latex] or positive. It makes sense that it must always be greater than any negative number.
The answer to this case is always all real numbers
Examples of How to Solve Absolute Value Inequalities
Example 1: Solve the absolute value inequality.
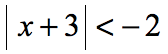
If you’re not familiar yet with the different cases, I suggest that you keep a copy of the list of cases above as a reference. This will definitely help you solve the problems easily.
The problem suggests that there exists a value of “[latex]x[/latex]” that can make the statement true. Well, the absolute value of something is always zero or positive which is never less than a negative number. This statement must be false, therefore, there is no solution. This is an example of case 3.
Pick some test values to verify:
- If [latex]x[/latex] is positive, say, [latex]x = 5[/latex];
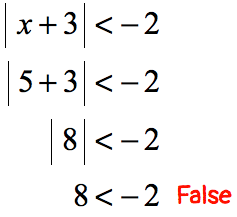
- If [latex]x[/latex] is zero;
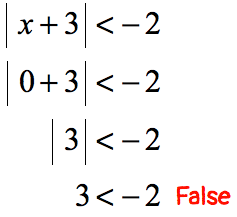
- If [latex]x[/latex] is negative, say, [latex]x = -5[/latex];
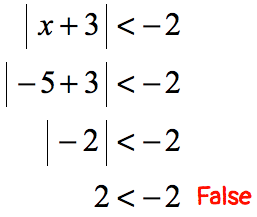
Example 2: Solve the absolute value inequality.
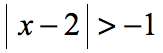
If you think about it, any values of “[latex]x[/latex]” can make the statement true. Test some numbers including zero, and any negative or positive number. What do you get?
Remember, the absolute value expression will yield a zero or positive answer which is always greater than a negative number. Therefore, the answer is all real numbers. This is case 4.
Example 3: Solve the absolute value inequality.
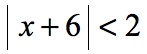
This is a “less than” absolute value inequality which is an example of case 1. Get rid of the absolute value symbol by applying the rule. Then solve the linear inequality that arises.

The goal is to isolate the variable “[latex]x[/latex]” in the middle. To do that, we subtract the left, middle, and right parts of the inequality by [latex]6[/latex].
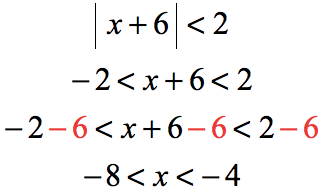
The answer in the form of the inequality symbol states that the solutions are all the values of [latex]x[/latex] between [latex]-8[/latex] and [latex]-4[/latex] but not including [latex]-8[/latex] and [latex]-4[/latex] themselves.
We can also write the answer in interval notation using parenthesis to denote that [latex]-8[/latex] and [latex]-4[/latex] are not part of the solutions.
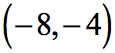
Or, write the answer on a number line where we use open circles to exclude [latex]-8[/latex] and [latex]-4[/latex] from the solution.

Example 4: Solve the absolute value inequality.
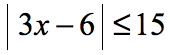
This is a “less than or equal to” absolute value inequality which still falls under case 1. Clear out the absolute value symbol using the rule and solve the linear inequality.
Isolate the variable “[latex]x[/latex]” in the middle by adding all sides by [latex]6[/latex] and then dividing by [latex]3[/latex] (coefficient of [latex]x[/latex]).
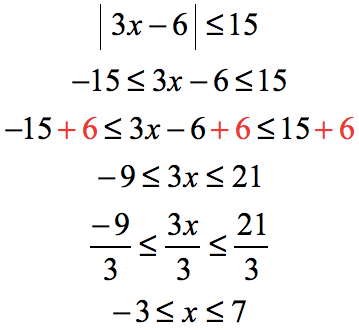
The inequality symbol suggests that the solution are all values of [latex]x[/latex] between [latex]-3[/latex] and [latex]7[/latex], and also including the endpoints [latex]-3[/latex] and [latex]7[/latex]. We include the endpoints because we are using the symbol “[latex]≤[/latex]”.
To write the answer in interval notation, we will utilize the square brackets instead of the regular parenthesis to denote that [latex]-3[/latex] and [latex]7[/latex] are part of the solution.
![[-3,7]](https://www.chilimath.com/wp-content/uploads/2019/01/absvalineq-ex4d.png)
And finally, we will use closed or shaded circles to show that [latex]-3[/latex] and [latex]7[/latex] are included.

Example 5: Solve the absolute value inequality.
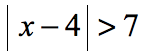
This is an example of a “greater than” absolute value inequality which is an example of case 2. Let’s eliminate the absolute value expression using the rule below.
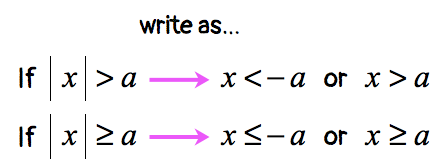
As you can see, we are solving two separate linear inequalities.
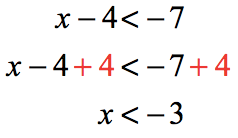
or
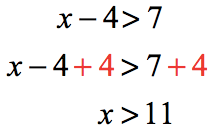
In interval notation, the word “or” is replaced by the symbol “[latex] \cup [/latex]” to mean “union“. The union of sets means that we are putting together the non-overlapping elements of two or more sets of solutions.
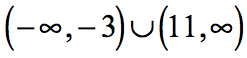
The answer in interval notation makes more sense if you see how it looks on the number line. In case 2, the arrows will always be in opposite directions. The open circles imply that [latex]-3[/latex] and [latex]7[/latex] are not included in the solutions which are the consequence of the symbol “[latex]>[/latex]”.

Example 6: Solve the absolute value inequality.
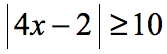
Break this up into two linear inequalities, and then solve each separately. Here’s the rule for case 2.
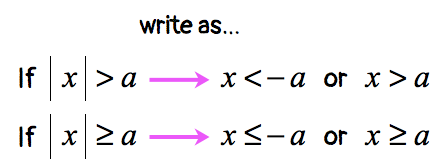
Here’s the solution.
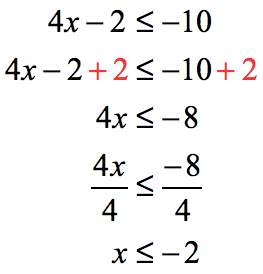
or
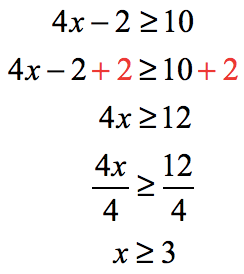
For the interval notation, we use the square brackets to include [latex]-2[/latex] and [latex]3[/latex] in the solution.
![(-∞, -2]U[3, ∞)](https://www.chilimath.com/wp-content/uploads/2019/01/absvalineq-ex6-d.png)
The shaded or closed circles signify that [latex]-2[/latex] and [latex]3[/latex] are part of the solution. In case 2, the arrows will always point to opposite directions.

You may also be interested in these related math lessons or tutorials:
