Volume of Sphere Formula
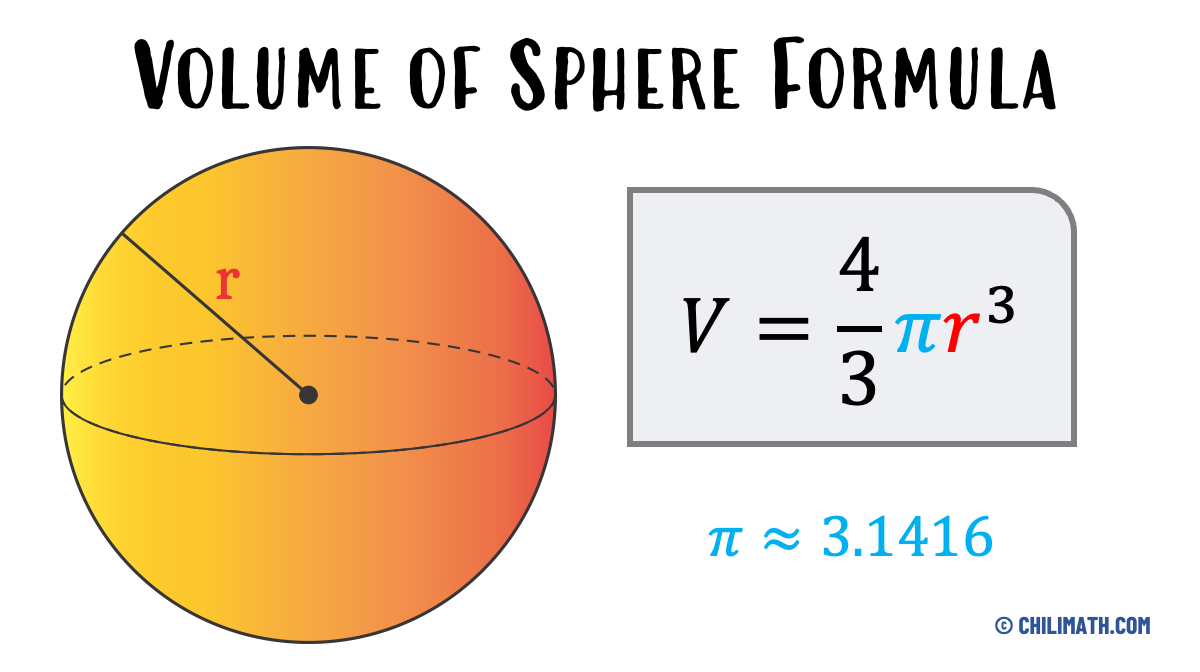
The volume of the sphere is the measure of space a sphere occupies within its surface as the boundary. Let’s think of a ball as a perfect sphere; loosely speaking, the amount of space that the air occupies inside the ball is its volume.
Don’t mixed things up between a circle and a sphere. They are two different geometric objects. A circle is a two-dimensional figure which means it can be drawn in a plane. You may think of a circle as flat object. On the other hand, there is no way we can draw a sphere on a plane because it lies on a three-dimensional space. It requires an additional axis z-axis that is perpendicular to the regular x and y axes.
Now, finding the volume of a sphere is easy. In order to calculate the volume of the sphere, all we need is its radius. Even if the radius is not given but just the diameter, we can still find the volume. Since the diameter is twice the radius, we can simply divide the diameter by [latex]2[/latex] to get the radius.
So here is the formula of the volume of the sphere if the radius [latex]r[/latex] is given:
[latex]\boxed{\large{V = {\large{{4 \over 3}}}\pi {{\color{red}{r}}^3}}}[/latex]
[latex]{\color{red}r} = {\text{radius}}[/latex]
[latex]\pi\approx3.14[/latex]
Note: Pi ([latex]\pi[/latex]) is the ratio of the circumference of the circle to its diameter. The value is an irrational number which is approximately equal to [latex]3.1416[/latex].
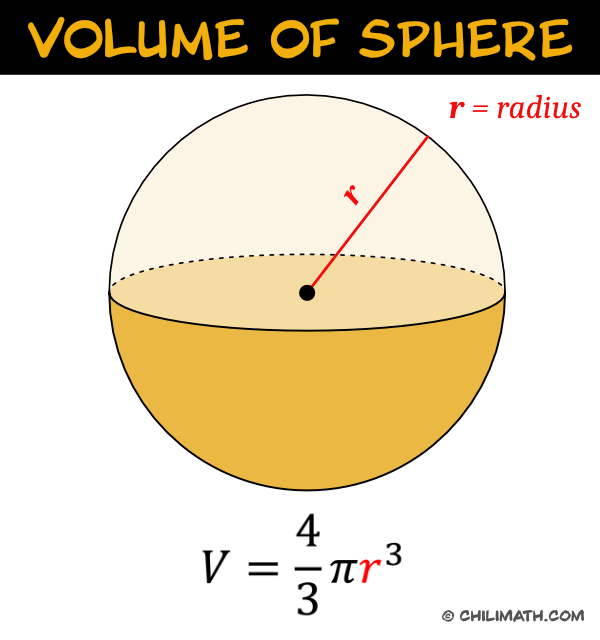
Examples of Finding the Volume of Sphere
Example 1: Find the volume of sphere with a radius of [latex]6[/latex] inches. Express your answer in terms of [latex]\pi[/latex].
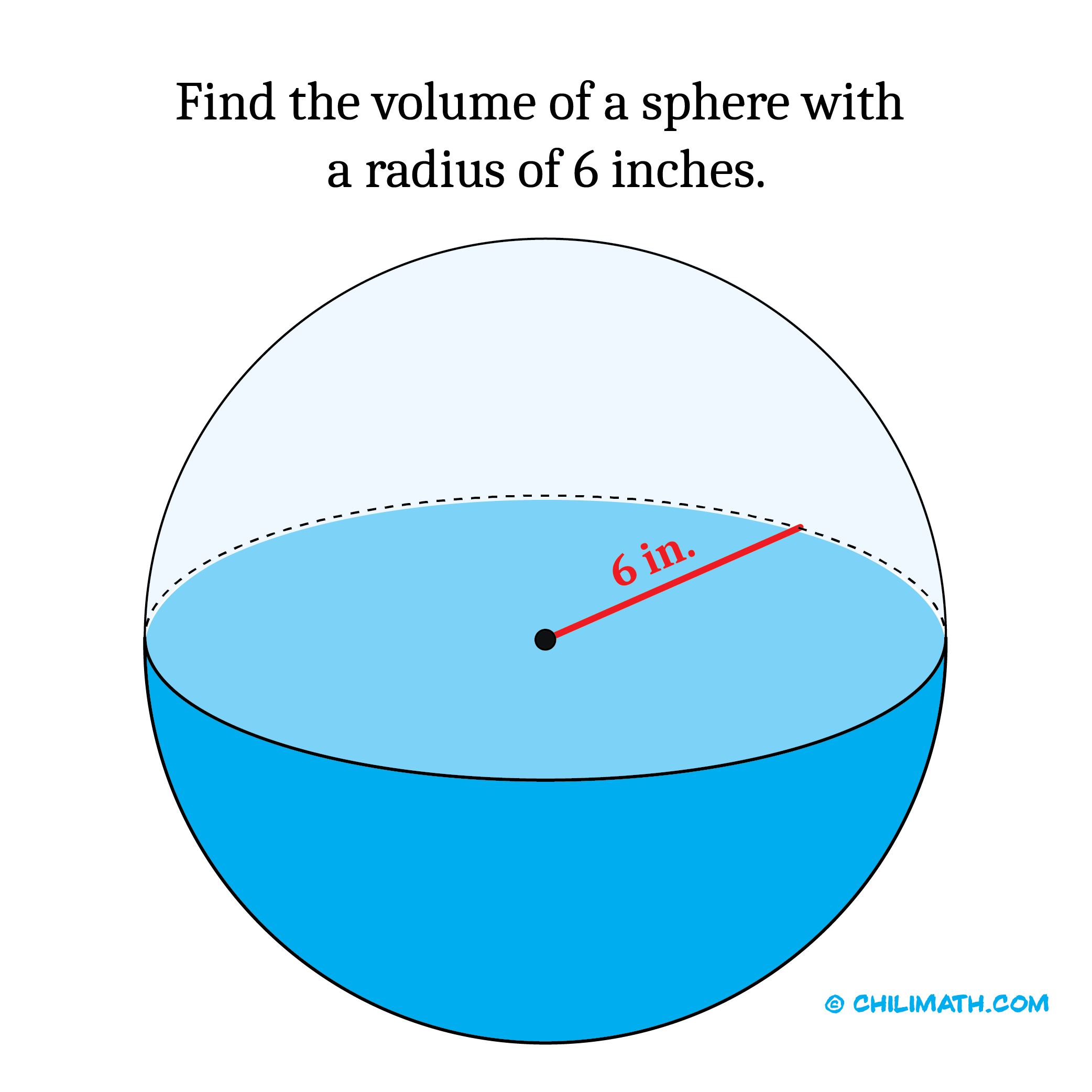
In this problem, the radius of the sphere is given to us which is [latex]r=6[/latex]. That makes our life very easy! We just need to substitute the value of radius into the formula then simplify.
However, we need to be extra careful when we give our final answer. In the problem, we’re told to express our answer in terms of pi, [latex]\pi[/latex]. This means when we leave the answer in terms of [latex]\pi[/latex], we’re giving the exact volume of the sphere. It’s different if we use the decimal approximation of [latex]\pi[/latex], like [latex]3.14[/latex]. In that case, we’re estimating the sphere’s volume.
To reiterate, in this problem, we want the exact volume of the sphere that’s why we are leaving the answer in terms of [latex]\pi[/latex].
So now we are going to substitute the value of the radius [latex]r=6[/latex] into the formula and then we simplify. Finally, we must not forget to attach the unit of measure which is cubic inches, [latex]\text{in}^3[/latex].
\begin{align*} V &= {4 \over 3}\pi {r^3} \\ \\ & = {4 \over 3}\pi {\left( {\color{red}6} \right)^3} \\ \\ & = {4 \over 3}\pi {\left( 6 \right)^3} \\ \\ & = {4 \over 3}\pi \left( {216} \right) \\ \\ & = {4 \over 3}\left( {216} \right)\pi \\ \\ V &= 288\pi \end{align*}Therefore, the volume of the sphere is [latex]288\pi[/latex] cubic inches [latex]\text{in}^3[/latex].
Example 2: Determine the volume of a sphere having a radius of [latex]3[/latex] meters. Round your answer to the nearest tenth. Use [latex]\pi=3.1416[/latex].
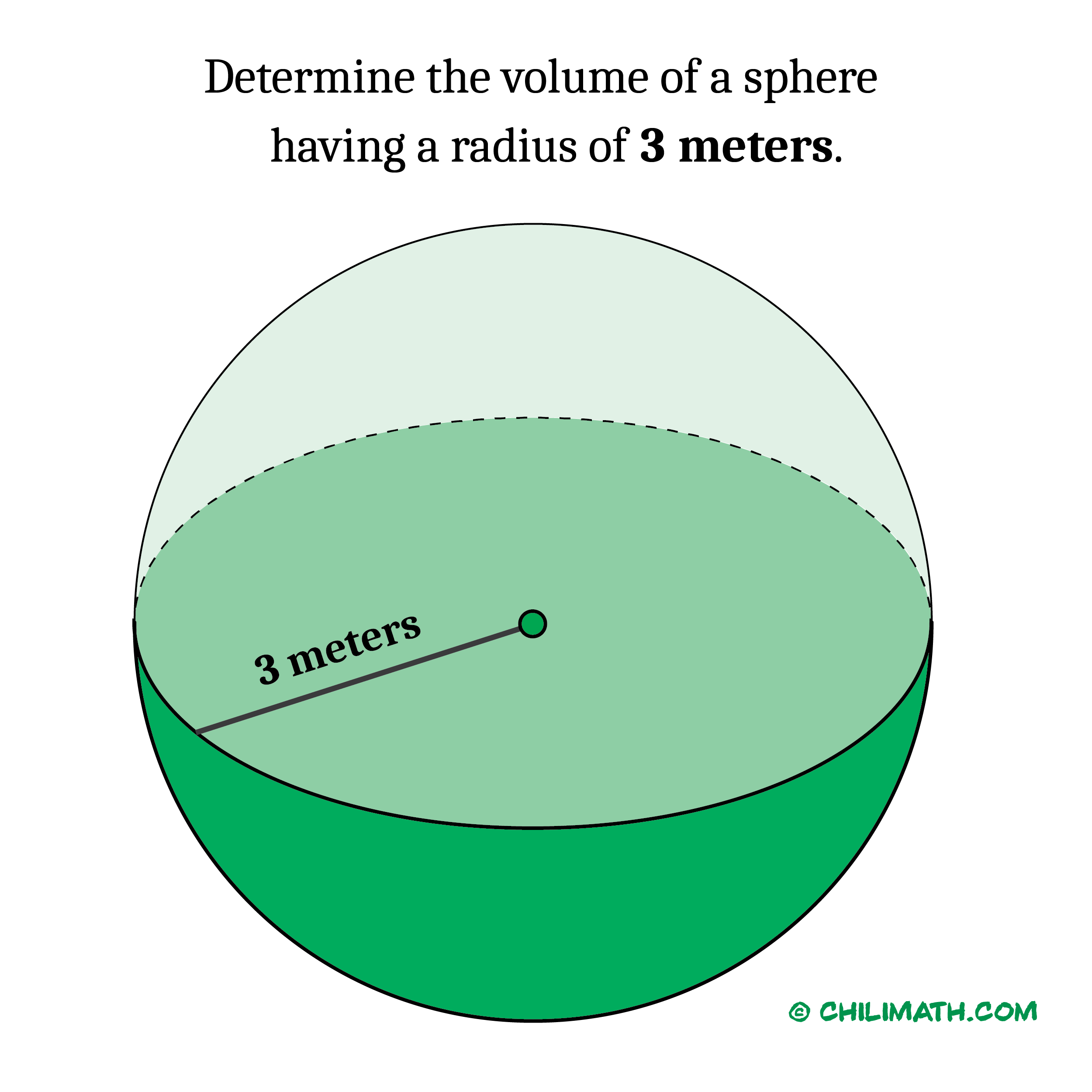
This problem is similar to example #1 because the radius of the sphere is given to us. However, the difference lies on the use of [latex]\pi[/latex]. In example #1, we leave our answer in terms of [latex]\pi[/latex] but in this problem we will use its approximate value of [latex]\pi = 3.1416[/latex]. Since we are using the estimated value of [latex]\pi[/latex], it follows that the volume of sphere here is also an approximation. Remember, we are also instructed to round it off to the nearest tenth. That means we round it to one decimal place. Finally, don’t forget to attach the unit of measure which is cubic meter [latex]\text{m}^3[/latex].
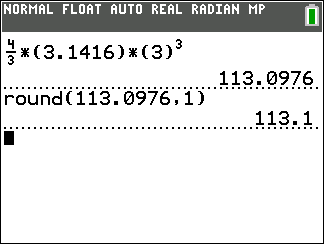
\begin{align*} V &= {4 \over 3}\pi {r^3} \\ \\ & = {4 \over 3}\left( {3.1416} \right){\left( 3 \right)^3} \\ \\ & = {4 \over 3}\left( {3.1416} \right)\left( {27} \right) \\ \\ & = {4 \over 3}\left( {27} \right)\left( {3.1416} \right) \\ \\ & = \left( {36} \right)\left( {3.1416} \right) \\ \\ V &\approx 113.1 \end{align*}Thus, the volume of the sphere is approximately [latex]113.1[/latex] cubic meters [latex]\text{m}^3[/latex].
Calculator check!
Example 3: Calculate the volume of sphere having a diameter of [latex]18[/latex] centimeters. Round your answer to the nearest whole number. Use [latex]\pi=3.14[/latex]
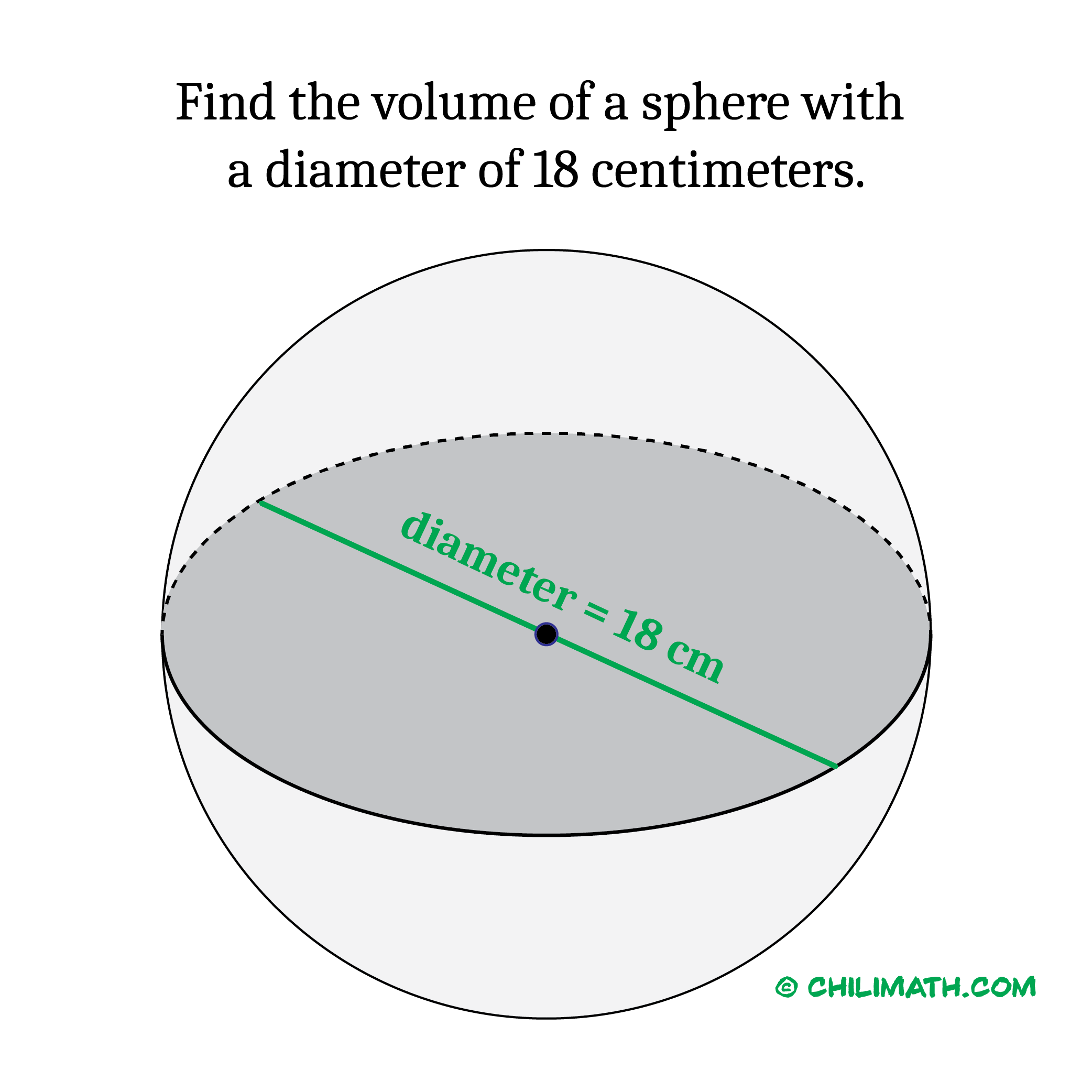
This time the diameter of the sphere is given, not the radius. Just remember the fact that the diameter is twice the radius, or the radius is half the diameter.
After finding the radius using the simple fact above, we can proceed as usual.
Be careful, though. Make sure that we follow the instructions. We are going to use the estimated value of [latex]\pi=3.14[/latex]. In addition, we will need to round off our final answer to the whole number.
Let’s go ahead and find the radius of the sphere. As we said, the radius is simply half the diameter.
\begin{align*} radius &= {1 \over 2}\left( {diameter} \right) \\ \\ & = {1 \over 2}\left( {18} \right) \\ \\ & = 9 \\ \\ radius &= 9 \end{align*}Now that we know what the radius is, we can plug in its value into the formula to compute the volume of the sphere.
\begin{align*} V &= {4 \over 3}\pi {r^3} \\ \\ & = {4 \over 3}\left( {3.14} \right){\left( 9 \right)^3} \\ \\ & = {4 \over 3}\left( {3.14} \right)\left( {729} \right) \\ \\ & = {4 \over 3}\left( {729} \right)\left( {3.14} \right) \\ \\ & = \left( {972} \right)\left( {3.14} \right) \\ \\ V &\approx 3,052 \end{align*}Therefore, the volume of the sphere is approximately [latex]3,052[/latex] cubic centimeters [latex]\text{cm}^3[/latex].
Calculator check!

Example 4: The volume of the sphere is [latex]5,207[/latex] cubic meters. What is the radius of the sphere? Round your answer to the nearest tenth. Use [latex]\pi=3.14[/latex].
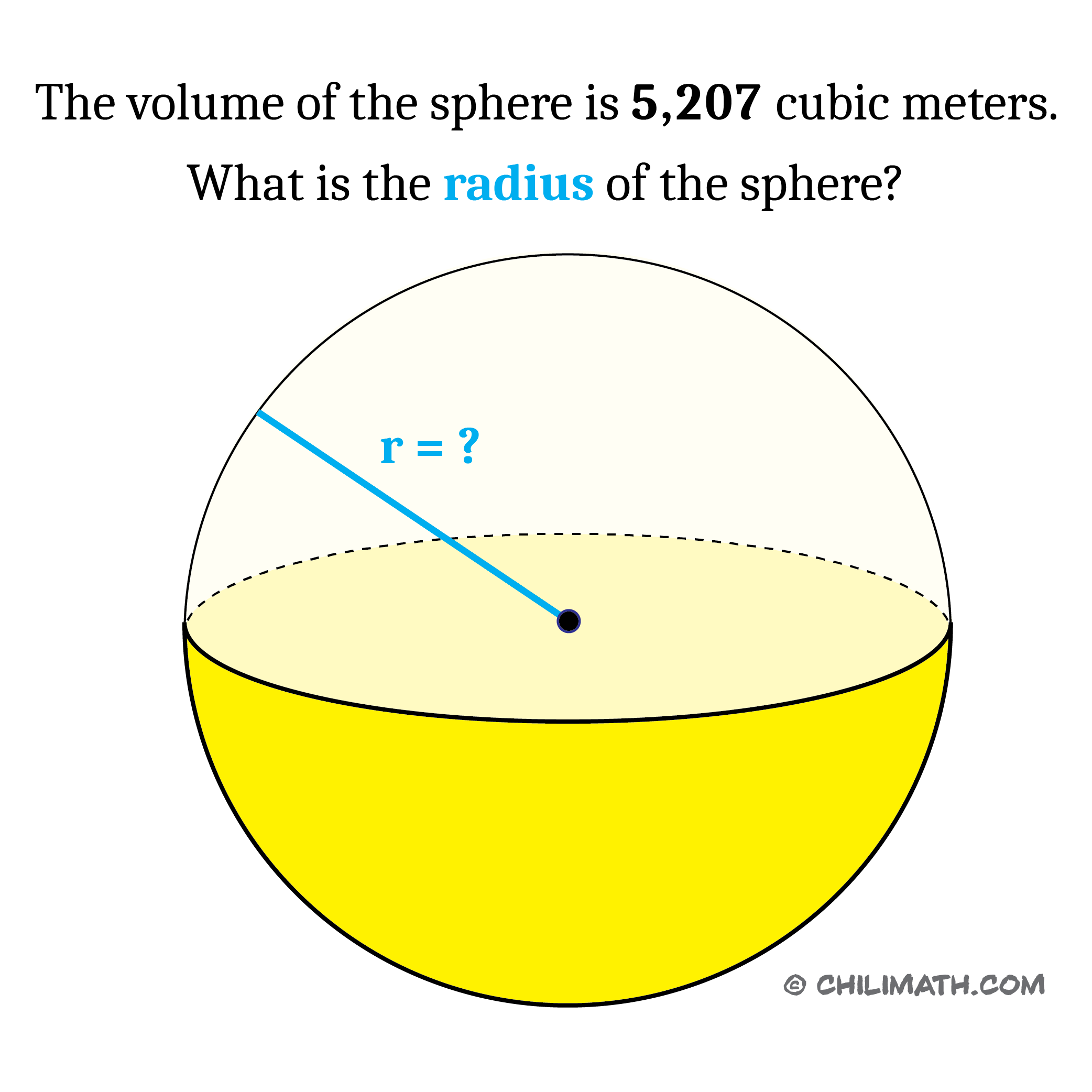
In this problem, we are not looking for the volume of the sphere. In fact, the volume of the sphere has already been provided to us. So what’s the deal then? The goal is to manipulate the formula to find the radius of the sphere.
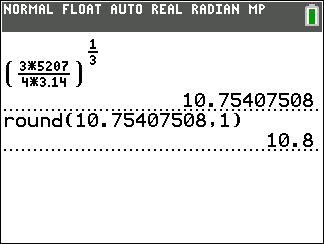
\begin{align*} V &= {4 \over 3}\pi {r^3} \\ \\ 5,207 &= {4 \over 3}\left( {3.14} \right){r^3} \\ \\ 5,207 &= {4 \over 3}\left( {3.14} \right){r^3} \\ \\ 15,621 &= 4\left( {3.14} \right){r^3} \\ \\ 15,621 &= \left( {12.56} \right){r^3} \\ \\ {{15,621} \over {12.56}} &= {r^3} \\ \\ {\left( {{{15,621} \over {12.56}}} \right)^{{1 \over 3}}} &= {r} \\ \\ 10.8 &\approx r \end{align*}Therefore, the radius of the sphere is approximately [latex]10.8[/latex] meters [latex]\text{m}[/latex].
Calculator check!
Example 5: If the radius of the sphere is doubled, what happens to the volume of the sphere?
Let’s suppose the radius of the original sphere is [latex]r[/latex] while the radius of the new sphere is [latex]{r}^\prime[/latex] (read as r prime).
Since the radius of the new sphere is twice the radius of the original sphere. We have the situation:
[latex]{r}^\prime = \color{red}2r[/latex]
Here’s the formula of the volume of the NEW sphere with twice the radius of the original.
\begin{align*} {V}^\prime = {4 \over 3}\pi {\left( {r}^\prime \right)^3} \end{align*}Now, let’s substitute [latex]\color{red}2r[/latex] for [latex]r^\prime[/latex].
\begin{align*} {V}^\prime &= {4 \over 3}\pi {\left( {{\color{red}2r}} \right)^3} \\ \\ & = {4 \over 3}\pi {\left( {\color{red}2} \right)^3}{\left( {\color{red}r} \right)^3} \\ \\ & = {4 \over 3}\pi \left( 8 \right)\left( {{r^3}} \right) \\ \\ &= 8\left( {{\color{blue}{4 \over 3}\pi {r^3}}} \right) \\ \\ {V}^\prime &=8{\color{blue}{V}} \end{align*}Therefore, if the radius of a sphere is doubled, the volume of the sphere becomes eight times or eight fold.
YOU TRY!
Example 6: If the radius of the sphere is tripled, what happens to the volume of the sphere?
Answer
If the radius is tripled, then the radius of the sphere becomes [latex]3r[/latex].
\begin{align*} {V}^\prime &= {4 \over 3}\pi {\left( {{\color{red}3r}} \right)^3} \\ \\ & = {4 \over 3}\pi {\left( {\color{red}3} \right)^3}{\left( {\color{red}r} \right)^3} \\ \\ & = {4 \over 3}\pi \left( 27 \right)\left( {{r^3}} \right) \\ \\ &= 27\left( {{\color{blue}{4 \over 3}\pi {r^3}}} \right) \\ \\ {V}^\prime &=27{\color{blue}{V}} \end{align*}Therefore, the volume of the sphere is increased by twenty-seven times.
Let’s do a final example. This one is a bit different but still related to this topic. The surface area of the sphere is given and we will have to figure out the volume of the same sphere.
For your information, below is the formula to find the surface area of a sphere.
[latex]\text{Surface Area of Sphere} = 4\pi {r^2}[/latex]
It may sound complex, but it’s really not. The key is to use the formula of the area of the sphere to determine the radius of the sphere. Then use the value of the radius to calculate its volume using the volume formula that we have been using from previous examples.
[latex]\text{Volume of Sphere} = {\large{4 \over 3}}\pi {r^3}[/latex]
Here we go!
Example 7: The surface area of a sphere is [latex]616[/latex] [latex]\text{ft}^2[/latex]. Find the volume of the sphere. Round you answer to two decimal places. Use [latex]\pi=22/7[/latex] as an approximation.
First, we write the formula for the surface area of the sphere ([latex]SA[/latex]). Then, we plug in the value of the area which is [latex]616[/latex] and solve for the radius [latex]r[/latex].
[latex]\boxed{SA = 4\pi {{\color{red}r}^2}}[/latex]
Let’s get started!
\begin{align*} SA &= 4\pi {r^2} \\ \\ 616 &= 4\left( {{{22} \over 7}} \right){r^2} \\ \\ 616\left( 7 \right) &= 4\left( {22} \right){r^2} \\ \\ 4,312 &= 88{r^2} \\ \\ {{4,312} \over {88}} &= {r^2} \\ \\ 49 &= {r^2} \\ \\ \sqrt {49} &= r \\ \\ 7 &= r \end{align*}Now that we found the radius of the sphere, it is time to calculate its volume. We have done this before so it’s no big deal. Here’s again the formula for the volume of sphere.
[latex]\boxed{\text{Volume of Sphere} = {\large{4 \over 3}}\pi {r^3}}[/latex]
Let’s substitute the radius that we have found above which is [latex]r=7[/latex].
\begin{align*} V &= {4 \over 3}\pi {r^3} \\ \\ & = {4 \over 3}\left( {{{22} \over 7}} \right){\left( {\color{red}7} \right)^3} \\ \\ & = {4 \over 3}\left( {{{22} \over 7}} \right)\left( {343} \right) \\ \\ & = \left( {{{88} \over {21}}} \right)\left( {343} \right) \\ \\ V &\approx 1,437.33 \end{align*}Hence, the volume of the sphere with a surface area of [latex]616[/latex] [latex]\text{ft}^2[/latex] is approximately [latex]1,437.33[/latex] [latex]\text{ft}^3[/latex].
Calculator check!
Find the radius of the sphere:
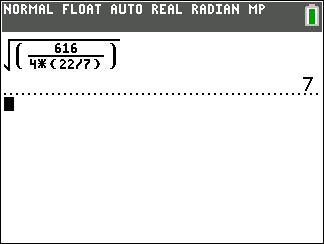
Find the volume of the sphere:
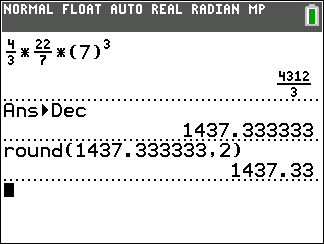
YOU TRY!
Example 8: If the surface area of the sphere is [latex]2,464[/latex] [latex]\text{m}^2[/latex], what is its volume? Round you answer to the nearest hundredth. Use [latex]\pi=22/7[/latex] as an approximation.
Answer
[latex]\boxed{SA = 4\pi {{\color{red}r}^2}}[/latex]
\begin{align*} SA &= 4\pi {r^2} \\ \\ 2,464 &= 4\left( {{{22} \over 7}} \right){r^2} \\ \\ 2,464\left( 7 \right) &= 4\left( {22} \right){r^2} \\ \\ 17,248 &= 88{r^2} \\ \\ {{17,248} \over {88}} &= {r^2} \\ \\ 196 &= {r^2} \\ \\ \sqrt {196} &= r \\ \\ 14 &= r \end{align*}Now, let’s find the volume using the radius [latex]r=14[/latex].
\begin{align*} V &= {4 \over 3}\pi {r^3} \\ \\ & = {4 \over 3}\left( {{{22} \over 7}} \right){\left( {14} \right)^3} \\ \\ & = {4 \over 3}\left( {{{22} \over 7}} \right)\left( {2,744} \right) \\ \\ & = \left( {{{88} \over {21}}} \right)\left( {2,744} \right) \\ \\ V &\approx 11,498.67 \end{align*}Therefore, the volume is approximately [latex]11,498.67[/latex] [latex]\text{m}^3[/latex].
You may also be interested in these related math lessons or tutorials:
