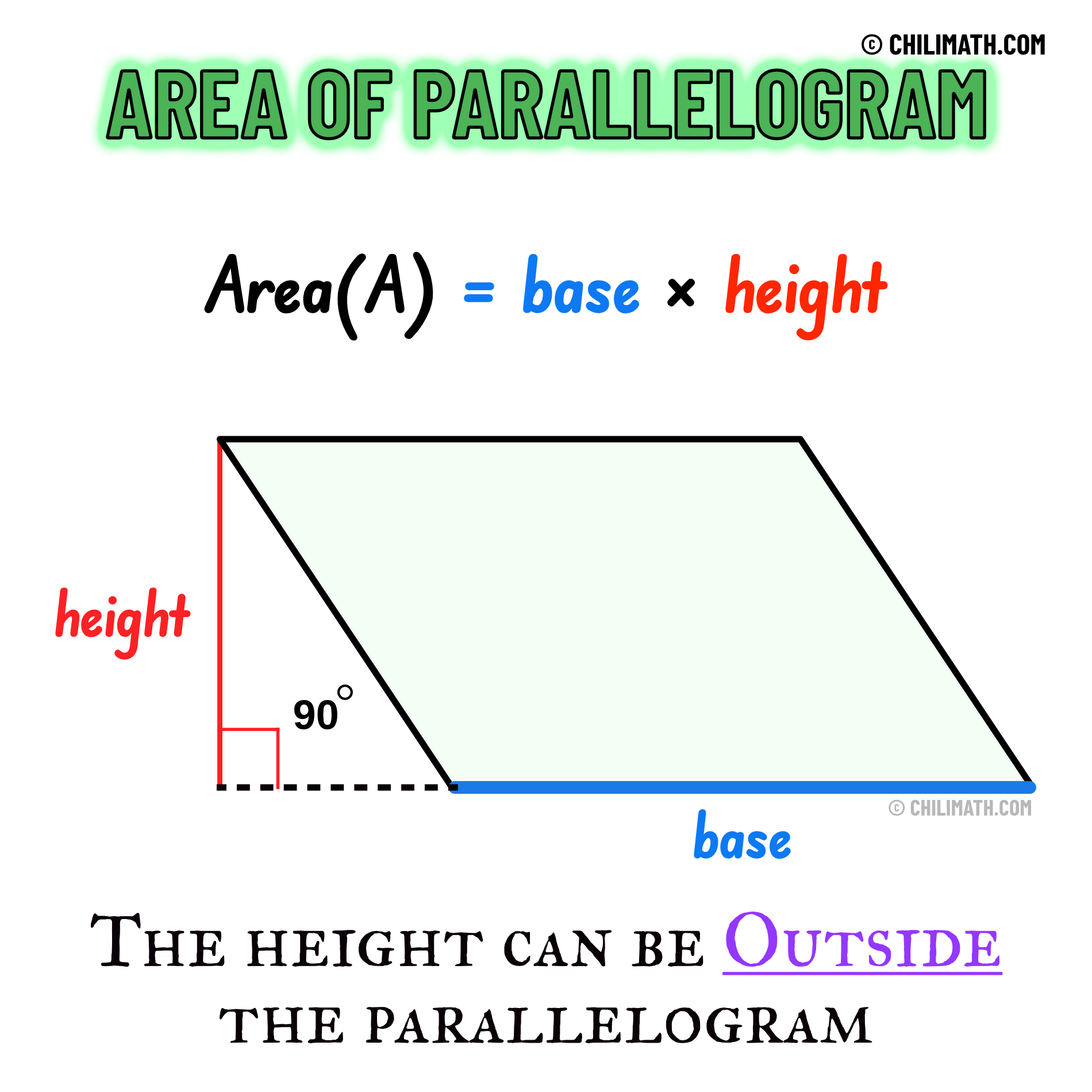
Area of Parallelogram Formula
A parallelogram is a quadrilateral (a four-sided polygon) such that the opposite sides are parallel. When it comes to the formula in finding the area of a parallelogram, we basically multiply the length of its base \(\color{blue}b\) by its corresponding height \(\color{red}h\), that is, \({\text{Area}} = {\color{blue}b} \times {\color{red}h}\). Yes, it’s pretty much like how we would calculate the area of a rectangle.
Before we proceed, we need to define the following terms:
- [latex]\color{blue}\textbf{base}[/latex] of a parallelogram – any side of a parallelogram
- [latex]\color{red}\textbf{height}[/latex] of a parallelogram – the corresponding height is the shortest perpendicular distance from the base to the opposite side or extended side
Notice that the height of the parallelogram (also known as altitude) can be found either internally or externally. In any case, the formula remains the same.
Height or Altitude Found Inside the Parallelogram

Height or Altitude Found Outside the Parallelogram
Height or Altitude Found Outside the Parallelogram
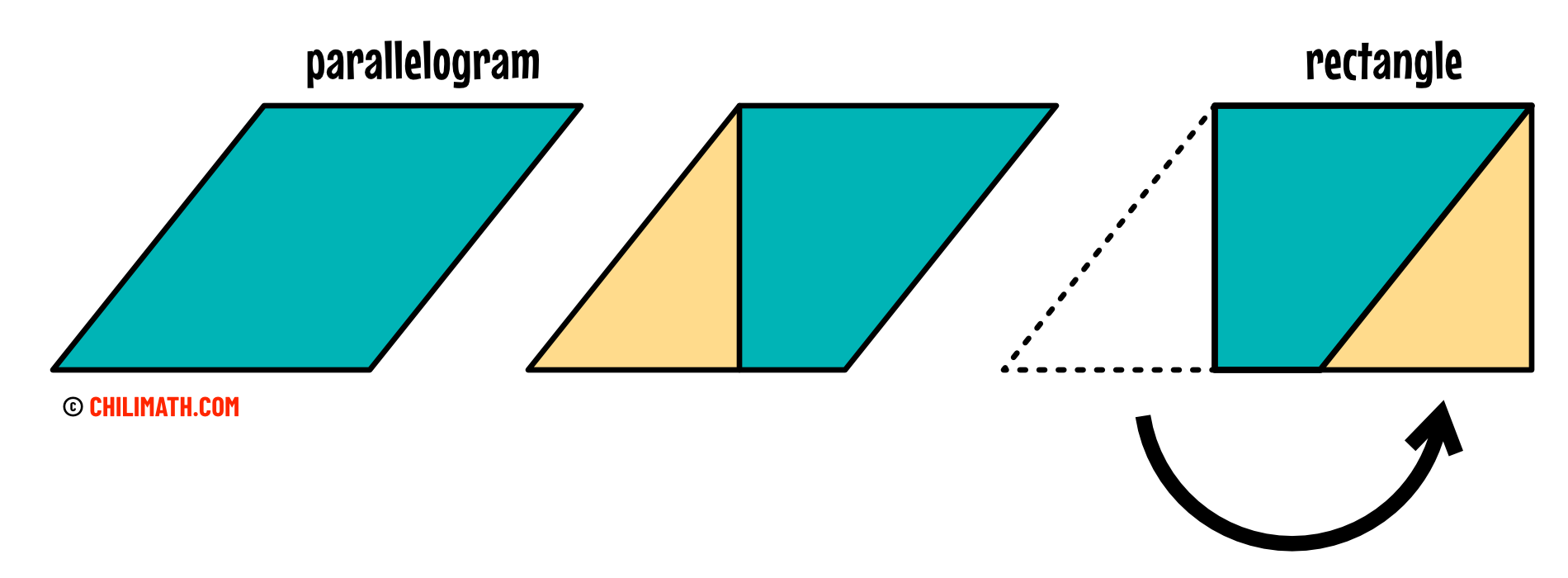
As I mentioned above, the formula to find the area of a parallelogram and a rectangle are practically the same. Why is that the case? Well, we can transform every parallelogram into a rectangle. Take a look at the two demonstrations below.
Observe that we can cut a piece from the parallelogram and rearrange it to form a rectangle.

Let’s go over some examples!
Examples of Finding the Area of Parallelogram
Example 1: Find the area of the parallelogram below by counting the squares. Verify the area by using the formula.

SOLUTION:
We can determine the area of the parallelogram by counting the squares that can fit inside its boundary. These squares are not just any squares; they have a side length of 1 unit. Therefore, each square has an area of [latex]1[/latex] square unit, that is, [latex]{\text{Area}} = 1{\text{unit}}^2[/latex].

To calculate the area of the parallelogram shown above, we must count both the complete squares and any half squares. It’s essential to remember that adding half of a square to another half makes up one whole square.
In the illustration above, for clarity I marked the complete or full squares with the number [latex]1[/latex] in blue color while the half squares with the fraction [latex]1/2[/latex] in pink color.
Now, we count the number of full or complete squares and the number of half squares. There are fifteen [latex]\text(15)[/latex] complete squares and ten [latex]\text(10)[/latex] half squares inside the parallelogram. Because two half squares make one complete square, then our ten [latex]\text(10)[/latex] half squares are equivalent to five [latex]\text(5)[/latex] complete squares. Now, if we add up all our squares we get [latex]15+5=20[/latex]. That means, there are twenty [latex]\text(20)[/latex] complete squares that fit inside the parallelogram!
\begin{align*} {A_P} &= 15 + {1 \over 2}\left( {10} \right) \\ & = 15 + 5 \\ & = \boxed{{\color{red}20}} \end{align*}Therefore, the area of the parallelogram is [latex]20[/latex] [latex]\text{unit}^2[/latex] or square units.
Let’s double-check using the parallelogram formula to see if we arrive at the same result. Now we want to identify the base and height of the parallelogram to substitute them into the formula. Here, for convenience, we chose the base as the bottom side with a measure of [latex]4[/latex] units. The height is [latex]5[/latex] units, determined as the perpendicular distance from the opposite side of the base. However, we extend the base to ensure this measurement is taken at a right angle.

Since the base is [latex]4[/latex] units and the height is [latex]5[/latex] units, we can plug in the values into the formula to calculate the area of the parallelogram:
\begin{align*} & b = {\color{blue}4}\,\, \text{units} \\ & h = {\color{red}5}\,\, \text{units} \\ \\ A &= bh \\ & = \left( {\color{blue}4} \right)\left( {\color{red}5 }\right) \\ & = 20 \\ A &= 20 \\ \end{align*}Therefore, the area of the parallelogram is [latex]20[/latex] square units.
Notice how we both arrived at the same conclusion! The areas we determined by counting squares and using the parallelogram formula are exactly the same!
Example 2: Determine the area of the parallelogram by counting the squares. Use the area formula of parallelogram to verify your answer.

We’ll work on a similar problem just like the one above to improve our skills. However, this time, we’ll try to solve it more quickly.
Let’s mark the complete square with [latex]\textbf{1}[/latex] and the half square with [latex]\textbf{1/2}[/latex]. Refer to the illustration below.

Let’s count the squares inside the parallelogram. First, we notice there are [latex]40[/latex] whole squares. Next, we see [latex]10[/latex] half squares, and since two halves make a whole, those [latex]10[/latex] half squares are equivalent to [latex]5[/latex] full squares. When we add them up, [latex]40 + 5[/latex] gives us [latex]45[/latex] full squares. So, by counting these full squares, we find that the parallelogram has an area of [latex]45[/latex] square units.
We can double-check our answer by applying the formula to calculate the area of the parallelogram.

Using the illustration above, clearly the height is [latex]5[/latex] units and the base is [latex]9[/latex] units.
\begin{align*} & b = {\color{blue}9}\,\,\text{units} \\ & h = {\color{red}5}\,\,\text{units} \\ \\ A &= bh \\ & = \left( {\color{blue}9} \right)\left( {\color{red}5} \right) \\ & = 45 \\ A &= 45 \\ \end{align*}Therefore, the area of the parallelogram is [latex]45\,{\text{unit}^2}[/latex].
Example 3: Find the area of the parallelogram below. Note: the drawing is not to scale.

The height is clearly [latex]4\,\text{ft}[/latex]. However, we need to be extra careful when identifying the base of the parallelogram. The base isn’t [latex]2\,\text{ft}[/latex] or [latex]6\,\text{ft}[/latex]. Instead, it’s the total length, which is the sum of [latex]2\,\text{ft}[/latex] and [latex]6\,\text{ft}[/latex], giving us [latex]8\,\text{ft}[/latex].
Therefore, the area of the parallelogram is [latex]32[/latex] [latex]\text{ft}^2[/latex].
Example 4: Given that the base of the parallelogram is [latex]7[/latex] meters wide, determine the height if its area is [latex]31.5[/latex] square meters.
To find the height of the parallelogram, we can use the formula for the area of a parallelogram:
[latex] \text{Area} = \text{base} \times \text{height} [/latex]
We know the base to be [latex]7[/latex] meters and the area as [latex]31.5[/latex] square meters.
We can plug these values into the formula:
[latex] 31.5 = 7 \times \text{height} [/latex]
To find the height, divide both sides of the equation by [latex]7[/latex]:
[latex] \text{height} = \frac{31.5}{7} = 4.5 \text{ meters} [/latex]
So, the height of the parallelogram is [latex]4.5[/latex] meters.