Area of a Circle Practice Problems with Answers

There are twelve (12) practice problems in this exercise about the area of the circle. You may use a calculator. Do not round intermediate calculations.

Round your final answer to two decimal places unless the exact answer is required.

For your convenience, I have included the different variations of formulas that you can use to find the area of a circle.

Three (3) formulas that you can use to find the area of a circle. The formulas are A=pi(r^2), A=((pi)d^2)/4, and A=C^2/(4pi)

Problem 1: What is the area of a circle with radius [latex]8[/latex] meters? Leave your answer in terms of [latex]\large{\pi}[/latex].

Answer

This problem requires us to leave our answer in terms of [latex]\pi[/latex].

[latex]64\pi [/latex] square meters

Problem 2: The diameter of a circle is [latex]4.5[/latex] feet. Find its area. Use [latex]\pi = 3.1416[/latex].

Answer

[latex]15.90[/latex] square feet

Problem 3: Find the area of the circle below with a given radius. Use [latex]\pi = 3.14[/latex]

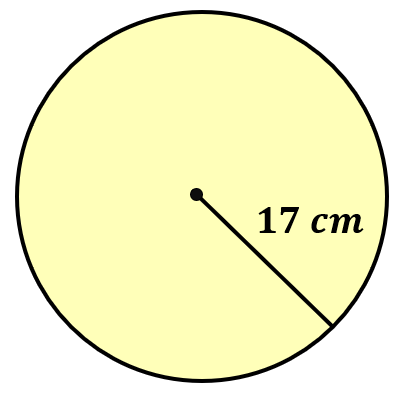
a circle with radius 17 centimeters
Answer

[latex]907.46[/latex] square centimeters

Problem 4: Find the area of the circle below with a given diameter. Use the value of [latex]\pi[/latex] on your calculator.

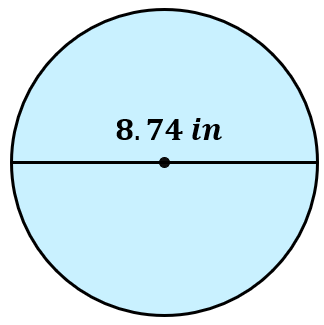
circle with radius 8.74 inches
Answer

Make sure that you use the internal value of [latex]\pi[/latex] on your calculator.

[latex]60.00[/latex] square inches

Problem 5: The circumference of a circle is [latex]22.2[/latex] feet. What is its area? Use [latex]\pi = 3.14[/latex]

Answer

[latex]39.24[/latex] square feet

Problem 6: Determine the area of a dinner plate with a circumference of [latex]37.68[/latex] inches. Use [latex]\pi = 3.14[/latex].

Answer

[latex]113.04[/latex] square inches

Problem 7: The radius of a circle is [latex]5[/latex] inches. Find the area of the circle expressed in square centimeters [latex]c{m^2}[/latex]. Use 1 in = 2.54 cm. Use [latex]\pi = 3.14[/latex].

Answer

Convert [latex]5[/latex] inches to centimeters.

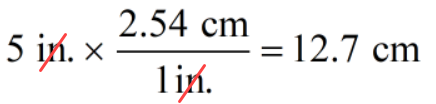
5 inches is equal to 12.7 centimeters

The area is

[latex]506.45[/latex] square centimeters

Problem 8: The diameter of a circle is [latex]12.4[/latex] miles. Calculate the area of the circle in terms of square kilometers [latex]k{m^2}[/latex]. Use 1 mi = 1.609 km. Use [latex]\pi = 3.1416[/latex].

Answer

Convert [latex]12.4[/latex] miles to kilometers.

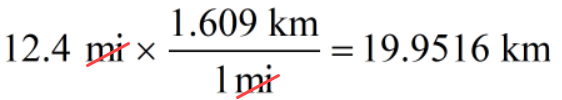
12.4 miles is equal to 19.9516 kilometers

The area is

[latex]312.64[/latex] square kilometers

Problem 9: What is the radius of a circle with an area of [latex]73.12[/latex] square miles [latex]m{i^2}[/latex]? Use [latex]\large{\pi = {{22} \over 7}}[/latex].

Answer

[latex]4.82[/latex] miles

Problem 10: Determine the diameter of the circle having an area of [latex]100[/latex] square yards [latex]y{d^2}[/latex]. Use [latex]\large{\pi = {{22} \over 7}}[/latex].

Answer

[latex]11.28[/latex] miles

Problem 11: Find the area of the semicircle below with a diameter of [latex]8[/latex] centimeters. Use [latex]\pi = 3.1416[/latex].

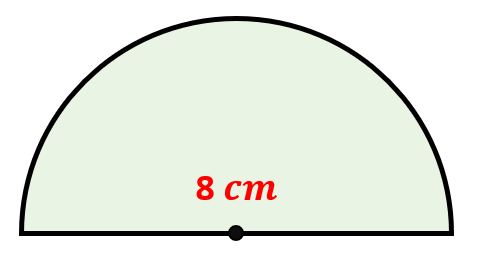
semicircle with a diameter of 8 diameters
Answer

The area of a semicircle is half of the area of a circle.

[latex]27.33[/latex] square centimeters

Problem 12: Both circles share the same center. Find the exact area of the shaded region.

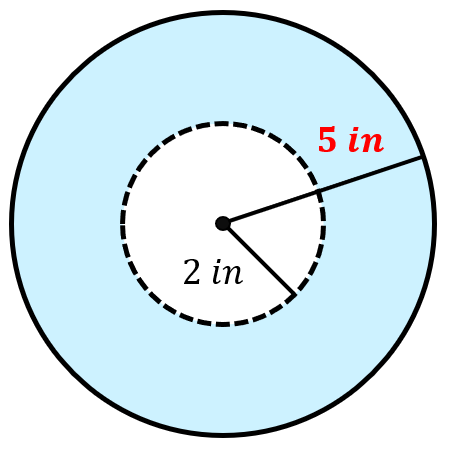
two circles that have the same center. the radius of the smaller circle is 2 inches while the larger circle is 5 inches.
Answer

Area of the shaded region = area of the larger circle minus area of the smaller (inner) circle

[latex]21\pi [/latex] square inches

You may also be interested in these related math lessons or tutorials:

Area of a Circle