Mathematical Induction for Summation

The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by contradiction. It is usually useful in proving that a statement is true for all the natural numbers [latex]\mathbb{N}[/latex]. In this case, we are going to prove summation statements that depend on natural numbers [latex]\mathbb{N}[/latex] or the positive integers [latex]\mathbb{Z}^+[/latex].

My other lesson on mathematical induction deals with proving divisibility statements.

Believe me, the steps of proving using mathematical induction can be challenging at first. But when you actually start doing it, you will realize that it is very intuitive and simple. After going through the examples below, you will gain good insights and confidence to tackle much more challenging mathematical induction problems that deal with summations.

---

---

Diagram of Mathematical Induction using Dominoes

---

Examples of Proving Summation Statements by Mathematical Induction

a) Check the basis step [latex]n=1[/latex] if it is true.

[latex]3= n\left( {2n + 1} \right)[/latex]

[latex]3 = 1\left[ {2\left( 1 \right) + 1} \right][/latex]

[latex]3 = 1\left( 3 \right)[/latex]

[latex]3 = 3[/latex]

Yes, it is true!

b) Assume the statement is true for [latex]n=k[/latex].

[latex]\color{red}3 + 7 + 11 + … + \left( {4k – 1} \right) = k\left( {2k + 1} \right)[/latex]

c) Now, we are going to prove that it is true for [latex]n=k+1[/latex].

[latex]3 + 7 + 11 + … + \left( {4k – 1} \right) + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right][/latex]

Notice that we can greatly simplify the equation using part b).

[latex]{\color{red}3 + 7 + 11 + … + \left( {4k – 1} \right)} + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right][/latex]

[latex]{\color{red}k\left( {2k + 1} \right)} + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right][/latex]

The next obvious step is to simplify both sides of the equation. But here’s the thing. We want to simplify the left-hand side (LHS) as much as possible while the right-hand side (RHS) with the least number of steps when simplifying.

There’s nothing wrong if we are heavy on simplifications on both sides as long as we can show that both sides are equal. But it is more elegant that we keep the least amount of simplification on the right side with the most on the left. You will understand this better the more you practice with mathematical induction.

Without touching the left side of the equation, we are going to simplify the right side a bit. Distribute [latex]2[/latex] into the binomial inside the parenthesis then add the numbers.

[latex]{\color{red}k\left( {2k + 1} \right)} + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left[ {2\left( {k + 1} \right) + 1} \right][/latex]

[latex]k\left( {2k + 1} \right) + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left( {2k + 2 + 1} \right)[/latex]

[latex]k\left( {2k + 1} \right) + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left( {2k + 3} \right)[/latex]

Now, it’s time to manipulate the left-hand side so it looks the same as the right-hand side. Apply the Distributive Property twice then combine like terms. Finally, factor out the trinomial. We are done!

[latex]k\left( {2k + 1} \right) + \left[ {4\left( {k + 1} \right) – 1} \right] = \left( {k + 1} \right)\left( {2k + 3} \right)[/latex]

[latex]2{k^2} + k + 4k + 3= \left( {k + 1} \right)\left( {2k + 3} \right)[/latex]

[latex]2{k^2} + 5k + 3= \left( {k + 1} \right)\left( {2k + 3} \right)[/latex]

[latex]\left( {k + 1} \right)\left( {2k + 3} \right)= \left( {k + 1} \right)\left( {2k + 3} \right)[/latex] ✔︎

We have shown that if the statement is true for [latex]n=k[/latex], then it is also true for [latex]n=k+1[/latex]. Therefore, the statement is true for all natural numbers.◾️

---

a) Verify the basis step; [latex]n=1[/latex] is true.

[latex] – 1 = {\Large{{n \over 2}}}\left( {3n – 5} \right)[/latex]

[latex] – 1 = {\Large{{1 \over 2}}}\left[ {3\left( 1 \right) – 5} \right] [/latex]

[latex] – 1 = {\Large{{1 \over 2}}}\left[ {3 – 5} \right][/latex]

[latex] – 1 = {\Large{{1 \over 2}}}\left( { – 2} \right)[/latex]

[latex] – 1 = – 1[/latex]

Yes, it is true!

b) Assume the statement is true for [latex]n=k[/latex].

[latex]\color{red} – 1 + 2 + 5 + … + \left( {3k – 4} \right) = {\Large{{k \over 2}}}\left( {3k – 5} \right)[/latex]

c) Now, we are going to show that it holds true for [latex]n=k+1[/latex].

[latex] – 1 + 2 + 5 + … + \left( {3k – 4} \right) + \left[ {3\left( {k + 1} \right) – 4} \right] = {\Large{{{k + 1} \over 2}}}\left[ {3\left( {k + 1} \right) – 5} \right][/latex]

We will use part b) to substitute it into the equation.

[latex]{\color{red} – 1 + 2 + 5 + … + \left( {3k – 4} \right)} + \left[ {3\left( {k + 1} \right) – 4} \right] = {\Large{{{k + 1} \over 2}}}\left[ {3\left( {k + 1} \right) – 5} \right][/latex]

[latex]{\color{red}{\Large{k \over 2}}\left( {3k – 5} \right)} + \left[ {3\left( {k + 1} \right) – 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3\left( {k + 1} \right) – 5} \right][/latex]

Let’s focus on simplifying the right side of the equation first.

[latex]{\Large{k \over 2}}\left( {3k – 5} \right) + \left[ {3\left( {k + 1} \right) – 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3\left( {k + 1} \right) – 5} \right][/latex]

[latex]{\Large{k \over 2}}\left( {3k – 5} \right) + \left[ {3\left( {k + 1} \right) – 4} \right] = {\Large{{k + 1} \over 2}}\left[ {3k + 3 – 5} \right][/latex]

[latex]{\Large{k \over 2}}\left( {3k – 5} \right) + \left[ {3\left( {k + 1} \right) – 4} \right] = {\Large{{k + 1} \over 2}}\left( {3k – 2} \right)[/latex]

It is time to simplify and manipulate the left-hand side to make it appear the same as the right side of the equation.

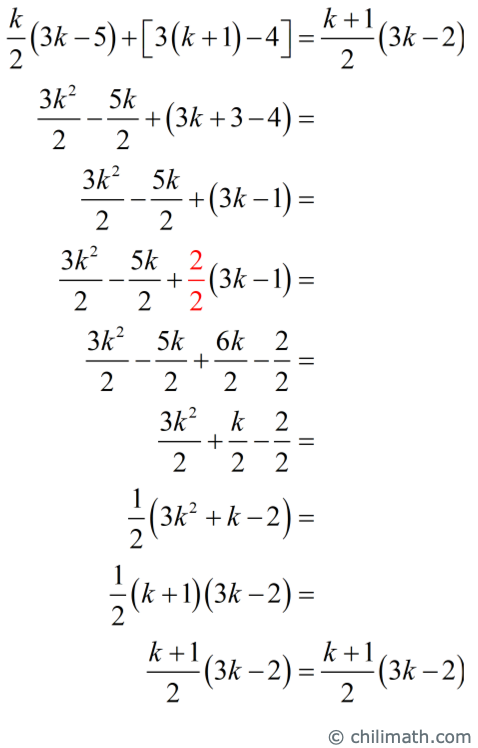
We have shown that if the statement is true for [latex]n=k[/latex], then it is also true for [latex]n=k+1[/latex]. Therefore, the statement is true for all natural numbers.◾️

---

a) Inspect the basis step; [latex]n=1[/latex] is true.

[latex]\large1 = {2^n} – 1[/latex]

[latex]\large 1 = {2^1} – 1[/latex]

[latex]\large1 = 2 – 1[/latex]

[latex]\large1 = 1 [/latex]

It is true!

b) Assume the statement is true for [latex]n=k[/latex].

[latex]\color{red}\large{1 + 2 + {2^2} + … + {2^{k – 1}} = {2^k} – 1 }[/latex]

c) If it is true for [latex]n=k[/latex], then it must be true for [latex]n=k+1[/latex].

[latex] \large1 + 2 + {2^2} + … + {2^{k – 1}} + {2^{\left( {k + 1} \right) – 1}} = {2^{k + 1}} – 1[/latex]

Use part b) to perform a substitution. This is the use of the assumption.

[latex] \large {\color{red}1 + 2 + {2^2} + … + {2^{k – 1}}} + {2^{\left( {k + 1} \right) – 1}} = {2^{k + 1}} – 1[/latex]

[latex] \large {\color{red} 2^{k}-1} + {2^{\left( {k + 1} \right) – 1}} = {2^{k + 1}} – 1[/latex]

There is no need to simplify the right-hand side. We will simplify and manipulate the left side of the equation so that it looks like the right side of the equation.

[latex] \large 2^{k}-1 + {2^{\left( {k + 1} \right) – 1}} = {2^{k + 1}} – 1[/latex]

Here we go!

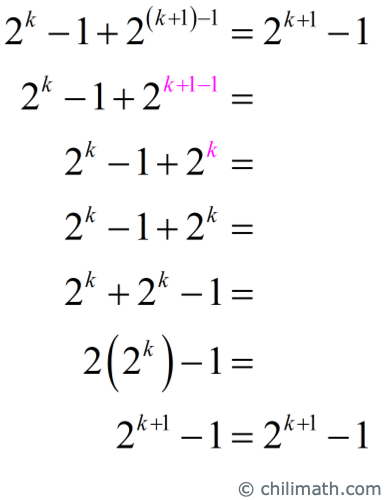
We have shown that if the statement is true for [latex]n=k[/latex], then it is also true for [latex]n=k+1[/latex]. Therefore, the statement is true for all natural numbers.◾️

---

a) Show the basis step; [latex]n=1[/latex] is true.

[latex]4 = {\Large{{n \over 2}}}\left( {5n + 3} \right)[/latex]

[latex]4 ={ \Large{{1 \over 2}}}\left[ {5\left( 1 \right) + 3} \right] [/latex]

[latex] 4 = {\Large{{1 \over 2}}}\left[ {5 + 3} \right][/latex]

[latex]4 ={ \Large{{1 \over 2}}}\left( 8 \right) [/latex]

[latex]4 = 4 [/latex]

Yes!

b) Assume true for [latex]n=k[/latex].

[latex]\color{red}4 + 9 + 14 + 19 + … + \left( {5k – 1} \right) = {\Large{{k \over 2}}}\left( {5k + 3} \right)[/latex]

c) If it is true for [latex]n=k[/latex], then [latex]n=k+1[/latex] must also be true.

[latex]4 + 9 + 14 + 19 + … + \left( {5k – 1} \right) + \left[ {5\left( {k + 1} \right) – 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right][/latex]

Perform a substitution using the information in part b). The seemingly complicated equation is going to be further simplified.

[latex]{\color{red}4 + 9 + 14 + 19 + … + \left( {5k – 1} \right)} + \left[ {5\left( {k + 1} \right) – 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right][/latex]

[latex]{\color{red}{\Large{{k \over 2}}}\left( {5k + 3} \right)} + \left[ {5\left( {k + 1} \right) – 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right][/latex]

Ignore the left side of the equation for now. We are going to clean up the right-hand side of the equation first by simplifying it.

[latex]{\Large{{k \over 2}}}\left( {5k + 3} \right) + \left[ {5\left( {k + 1} \right) – 1} \right] = {\Large{{{k + 1} \over 2}}}\left[ {5\left( {k + 1} \right) + 3} \right][/latex]

[latex]{\Large{{k \over 2}}}\left( {5k + 3} \right) + \left[ {5\left( {k + 1} \right) – 1} \right] = {\Large{{{k + 1} \over 2}}}\left( {5k + 5 + 3} \right)[/latex]

[latex]{\Large{{k \over 2}}}\left( {5k + 3} \right) + \left[ {5\left( {k + 1} \right) – 1} \right] = {\Large{{{k + 1} \over 2}}}\left( {5k + 8} \right)[/latex]

Our final step is to algebraically manipulate the left-hand side of the equation so that it becomes equal to the right-hand side.

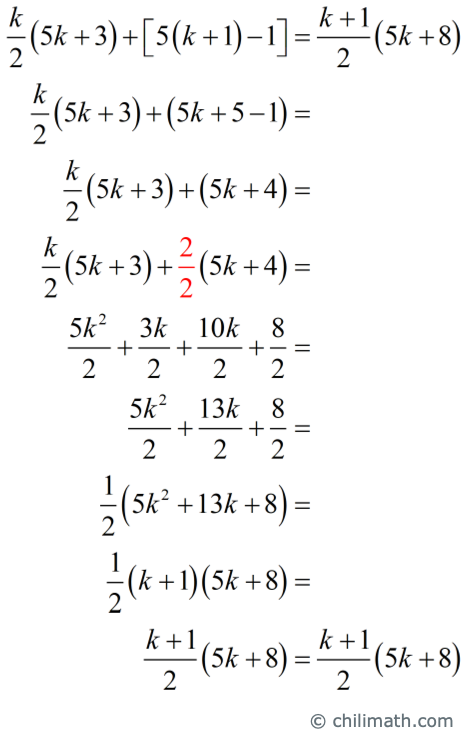
We have shown that if the statement is true for [latex]n=k[/latex], then it is also true for [latex]n=k+1[/latex]. Therefore, the statement is true for all positive integers.◾️

---

a) Show that the basis step is true for [latex]n=1[/latex].

[latex]\Large{1 \over {1 \cdot 2}} = {n \over {n + 1}}[/latex]

[latex]\Large{1 \over 2} = {n \over {n + 1}}[/latex]

[latex]\Large{1 \over 2} = {1 \over {1 + 1}} [/latex]

[latex]\Large{1 \over 2} = {1 \over 2}[/latex]

It is true!

b) Assume true for [latex]n=k[/latex].

[latex]\color{red}\Large{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \over {k\left( {k + 1} \right)}} = {k \over {k + 1}}[/latex]

c) Now, we are going to show that it will hold true for [latex]n=k+1[/latex].

[latex]\Large{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \over {k\left( {k + 1} \right)}} + {1 \over {\left( {k + 1} \right)\left[ {\left( {k + 1} \right) + 1} \right]}} = {{k + 1} \over {\left( {k + 1} \right) + 1}}[/latex]

Use the assumption written in part b) to perform a substitution. This will greatly simplify the equation we are working on.

[latex]\Large{\color{red}{1 \over {1 \cdot 2}} + {1 \over {2 \cdot 3}} + {1 \over {3 \cdot 4}} + … + {1 \over {k\left( {k + 1} \right)}}} + {1 \over {\left( {k + 1} \right)\left[ {\left( {k + 1} \right) + 1} \right]}} = {{k + 1} \over {\left( {k + 1} \right) + 1}}[/latex]

[latex]\Large{\color{red}{k \over {k + 1}}} + {1 \over {\left( {k + 1} \right)\left[ {\left( {k + 1} \right) + 1} \right]}} = {{k + 1} \over {\left( {k + 1} \right) + 1}}[/latex]

Without paying attention to the left side of the equation, let’s simplify the right side.

[latex]\Large{k \over {k + 1}} + {1 \over {\left( {k + 1} \right)\left[ {\left( {k + 1} \right) + 1} \right]}} = {{k + 1} \over {\left( {k + 1} \right) + 1}}[/latex]

[latex]\Large{k \over {k + 1}} + {1 \over {\left( {k + 1} \right)\left[ {\left( {k + 1} \right) + 1} \right]}} = {{k + 1} \over {k + 1 + 1}}[/latex]

[latex]\Large{k \over {k + 1}} + {1 \over {\left( {k + 1} \right)\left[ {\left( {k + 1} \right) + 1} \right]}} = {{k + 1} \over {k + 2}}[/latex]

To finish this off, we will manipulate the left-hand side of the equation such that it equals the right-hand side.

We have shown that if the statement is true for [latex]n=k[/latex], then it is also true for [latex]n=k+1[/latex]. Therefore, the statement is true for all positive integers.◾️

---

a) Check the basis step if [latex]n=1[/latex] is true.

[latex]\LARGE{1 \over 2} = {{{2^n} – 1} \over {{2^n}}}[/latex]

[latex]\LARGE{1 \over 2} = {{{2^1} – 1} \over {{2^1}}}[/latex]

[latex]\LARGE{1 \over 2} = {{2 – 1} \over 2}[/latex]

[latex]\LARGE{1 \over 2} = {1 \over 2}[/latex]

Yes, it is true!

b) Assume true for [latex]n=k[/latex].

[latex]\LARGE\color{red}{1 \over 2} + {1 \over 4} + {1 \over 8} + … + {1 \over {{2^k}}} = {{{2^k} – 1} \over {{2^k}}}[/latex]

c) Prove that it is true for [latex]n=k+1[/latex].

[latex]\LARGE{1 \over 2} + {1 \over 4} + {1 \over 8} + … + {1 \over {{2^k}}} + {1 \over {{2^{k + 1}}}} = {{{2^{k + 1}} – 1} \over {{2^{k + 1}}}}[/latex]

Use the assumption to make a substitution in order to simplify the equation.

[latex]\LARGE{\color{red}{1 \over 2} + {1 \over 4} + {1 \over 8} + … + {1 \over {{2^k}}}} + {1 \over {{2^{k + 1}}}} = {{{2^{k + 1}} – 1} \over {{2^{k + 1}}}}[/latex]

[latex]\LARGE{\color{red}{{{2^k} – 1} \over {{2^k}}}} + {1 \over {{2^{k + 1}}}} = {{{2^{k + 1}} – 1} \over {{2^{k + 1}}}}[/latex]

We will keep the right-hand side unchanged because it is simplified enough. We will work on the left-hand side to make it look the same as the one on the right.

We have shown that if the statement is true for [latex]n=k[/latex], then it is also true for [latex]n=k+1[/latex]. Therefore, the statement is true for all positive integers.◾️

---

You may also be interested in these related math lessons or tutorials:

Mathematical Induction (Divisibility)