Mathematical Induction for Divisibility
In this lesson, we are going to prove divisibility statements using mathematical induction. If this is your first time doing a proof by mathematical induction, I suggest that you review my other lesson which deals with summation statements. The reason is students who are new to the topic usually start with problems involving summations followed by problems dealing with divisibility.
Steps to Prove by Mathematical Induction
- Show the basis step is true. That is, the statement is true for [latex]n=1[/latex].
- Assume the statement is true for [latex]n=k[/latex]. This step is called the induction hypothesis.
- Prove the statement is true for [latex]n=k+1[/latex]. This step is called the induction step
What does it mean by [latex]a[/latex] divides [latex]b[/latex] ?
Since we are going to prove divisibility statements, we need to know when a number is divisible by another. So how do we know for sure if one divides the other?
Suppose [latex]\color{blue}\Large{a}[/latex] and [latex]\color{blue}\Large{b}[/latex] are integers. If [latex]\color{blue}\Large{a}[/latex] divides [latex]\color{blue}\Large{b}[/latex] , then we can write it as an equation
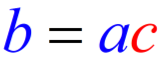
where [latex]\color{red}\Large{c}[/latex] is some integer.
Let’s go over some concrete examples.
- [latex]2[/latex] divides [latex]10[/latex] because [latex]10=2{\color{red}(5)}[/latex] where [latex]\color{red}5[/latex] is an integer
- [latex]8[/latex] divides [latex]136[/latex] because [latex]136=8{\color{red}(17)}[/latex] where [latex]\color{red}17[/latex] is an integer
- [latex]11[/latex] divides [latex]143[/latex] implies [latex]143=11{\color{red}(13)}[/latex] where [latex]\color{red}13[/latex] is an integer
- [latex]17[/latex] divides [latex]323[/latex] implies [latex]323=17{\color{red}(19)}[/latex] where [latex]\color{red}19[/latex] is an integer
Examples of Proving Divisibility Statements by Mathematical Induction
Example 1: Use mathematical induction to prove that [latex]\large{n^2} + n[/latex] is divisible by [latex]\large{2}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Basis step: show true for [latex]n=1[/latex].
[latex]{n^2} + n = {\left( 1 \right)^2} + 1[/latex]
[latex] = 1 + 1[/latex]
[latex] = 2[/latex]
Yes, [latex]2[/latex] is divisible by [latex]2[/latex].
b) Assume that the statement is true for [latex]n=k[/latex]. Thus, [latex]{n^2} + n[/latex] becomes [latex]{k^2} + k[/latex] where [latex]k[/latex] is a positive integer.
Now, write [latex]{k^2} + k[/latex] as part of an equation which denotes that it is divisible by [latex]2[/latex].
[latex]{k^2} + k = 2x[/latex]
for some integer [latex]x[/latex].
Solve for [latex]\color{red}k^2[/latex]. We will use this for substitution later.
[latex]{\color{red}{k^2}} = 2x – k[/latex]
c) Prove the statement is true for [latex]n=k+1[/latex].
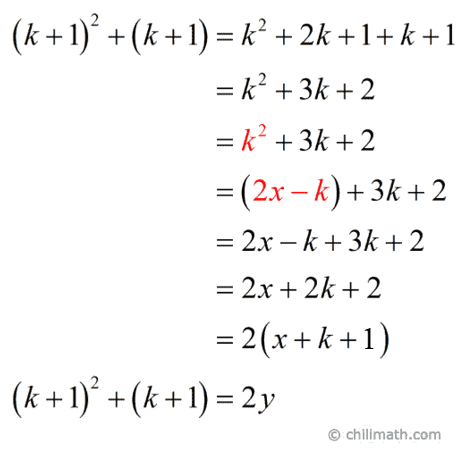
Where [latex]y = x + k + 1[/latex], and since [latex]x[/latex] and [latex]k[/latex] are integers, therefore [latex]y[/latex] is also an integer.
This means that [latex]{\left( {k + 1} \right)^2} + \left( {k + 1} \right)[/latex] is also divisible by [latex]2[/latex].
[latex]\therefore[/latex] By principle of mathematical induction, the statement is true for all positive integers.
Example 2: Use mathematical induction to prove that [latex]\large{n^3} – n + 3[/latex] is divisible by [latex]\large{3}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Is it true for [latex]n=1[/latex]?
[latex]{n^3} – n + 3 = {\left( 1 \right)^3} – \left( 1 \right) + 3[/latex]
[latex] = 1 – 1 + 3[/latex]
[latex] = 3[/latex]
Yes, it is divisible by [latex]3[/latex].
b) Assume true for [latex]n=k[/latex].
[latex]{n^3} – n + 3[/latex] → [latex]{k^3} – k + 3[/latex] where [latex]k \in \mathbb{Z}^+ [/latex]
Next, express [latex]{k^3} – k + 3[/latex] as part of an equation which suggests that it is divisible by [latex]3[/latex].
[latex]{k^3} – k + 3=3x[/latex]
for some integer [latex]x[/latex]
Solve for [latex]\color{red}k^3[/latex]. This will be used for substitution later.
[latex]{\color{red}{k^3}} = 3x + k – 3[/latex]
c) Show that the statement is true for [latex]n=k+1[/latex].
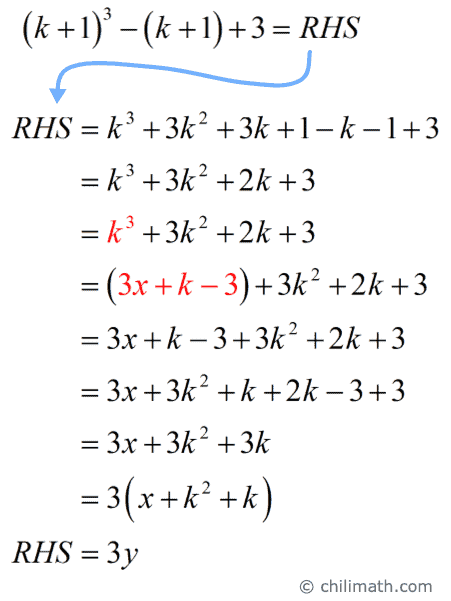
Notice, [latex]y = x + {k^2} + k[/latex]. Since [latex]x[/latex] and [latex]k[/latex] are integers, then [latex]y[/latex] must also be an integer.
We have shown that [latex]{\left( {k + 1} \right)^3} – \left( {k + 1} \right) + 3[/latex] is divisible by [latex]3[/latex].
[latex]\therefore[/latex] By the principle of mathematical induction, the statement is true for all positive integers.
Example 3: Use mathematical induction to prove that [latex]\large{2^{2n}} – 1[/latex] is divisible by [latex]\large{3}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Basis step: show the statement is true for [latex]n=1[/latex].
[latex]{2^{2n}} – 1 = {2^{2\left( 1 \right)}} – 1[/latex]
[latex] = {2^2} – 1[/latex]
[latex] = 4 – 1[/latex]
[latex] = 3[/latex]
Yes, it is divisible by [latex]3[/latex].
b) Assume the statement is true for [latex]n=k[/latex].
Substitute [latex]k[/latex] for [latex]n[/latex] to transform [latex]\large{2^{2n}} – 1[/latex] to [latex]\large{2^{2k}} – 1[/latex].
Suppose [latex]k[/latex] is a positive integer, if [latex]\large{2^{2k}} – 1[/latex] is divisible by [latex]3[/latex] then there exists an integer [latex]x[/latex] such that
[latex]\large{2^{2k}} – 1 = 3{\color{blue}x}[/latex]
Let’s solve for [latex]\large\color{red}{2^{2k}}[/latex]. This will be used in our inductive step in part c.
[latex]\large{\color{red}{2^{2k}}} = 3x + 1[/latex]
c) Prove the statement true for [latex]n=k+1[/latex].
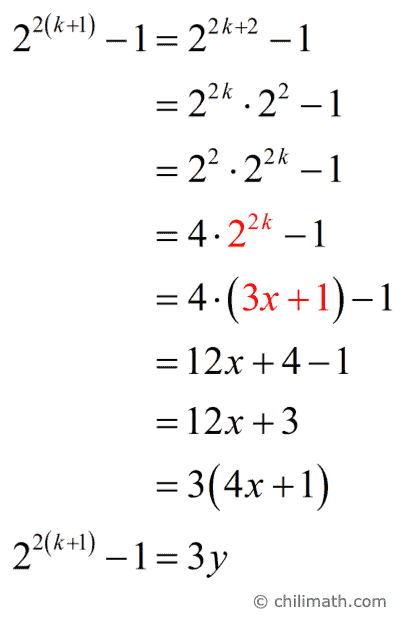
Note, [latex]y=4x+1[/latex]. I hope you can see that [latex]y[/latex] is an integer since [latex]x[/latex] is also an integer.
Clearly, [latex]\large{2^{2\left( {k + 1} \right)}} – 1[/latex] is divisible by [latex]3[/latex].
[latex]\therefore[/latex] By the principle of mathematical induction, the statement is true for all positive integers.
Example 4: Use mathematical induction to prove that [latex]\large{9^n} + 3[/latex] is divisible by [latex]\large{4}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Is it true for [latex]n=1[/latex]?
[latex]\large{9^n} + 3 = {9^1} + 3[/latex]
[latex]\large = 9 + 3[/latex]
[latex]\large = 12[/latex]
Yes, [latex]12[/latex] is divisible by [latex]4[/latex].
b) Assume the statement is true for [latex]n=k[/latex].
Replace [latex]n[/latex] by [latex]k[/latex], thus we have [latex]\large{9^k} + 3[/latex]. Now, write [latex]\large{9^k} + 3[/latex] in an equation showing that it is divisible by [latex]4[/latex].
Suppose [latex]k[/latex] is a positive integer, if [latex]\large{9^k} + 3[/latex] is divisible by [latex]4[/latex] then there exists an integer [latex]x[/latex] such that
[latex]\large{9^k} + 3 = 4{\color{blue}x}[/latex]
Solve for [latex]\large\color{red}{9^k}[/latex].
[latex]\large{\color{red}{9^k}} = 4x – 3[/latex]
c) Prove the statement true for [latex]n=k+1[/latex].
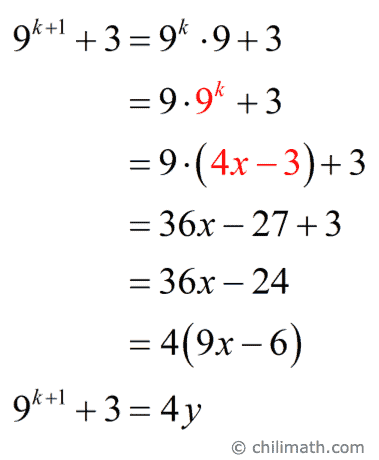
Where [latex]y = 9x – 6[/latex] and [latex]y[/latex] is an integer because [latex]x[/latex] is some integer.
This means [latex]\large{9^{k + 1}} + 3[/latex] is divisible by [latex]4[/latex].
[latex]\therefore[/latex] By the principle of mathematical induction, the statement is true for all positive integers.
Example 5: Use mathematical induction to prove that [latex]\large{8^n} – {3^n}[/latex] is divisible by [latex]\large{5}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Basis step: show true for [latex]n=1[/latex].
[latex]\large{8^n} – {3^n} = {8^1} – {3^1}[/latex]
[latex]\large = 8 – 3[/latex]
[latex]\large = 5[/latex]
Yes, it is divisible by [latex]5[/latex].
b) Assume the statement is true for [latex]n=k[/latex].
Transform [latex]\large{8^n} – {3^n}[/latex] to [latex]\large{8^k} – {3^k}[/latex].
Write [latex]\large{8^k} – {3^k}[/latex] in an equation expressing that it is divisible by [latex]5[/latex].
[latex]\large{8^k} – {3^k}=5{\color{blue}x}[/latex]
for some positive integer [latex]x[/latex]
Solve for [latex]\large\color{red}{8^k}[/latex]. We will use this for substitution in part c.
[latex]\large{\color{red}{8^k}} = 5x + {3^k}[/latex]
c) Prove the statement is true for [latex]n=k+1[/latex].
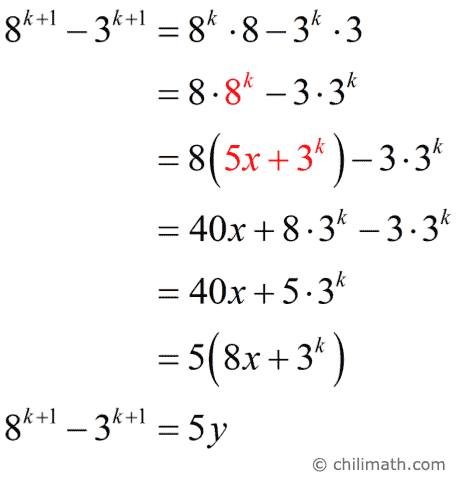
where [latex]\large{y={8x + {3^k}}}[/latex]
[latex]y[/latex] is some integer since [latex]x[/latex] and [latex]k[/latex] are integers
We have shown that [latex]\large{8^{k + 1}} – {3^{k + 1}}[/latex] is divisible by [latex]5[/latex].
[latex]\therefore[/latex] By the principle of mathematical induction, the statement is true for all positive integers.
Example 6: Use mathematical induction to prove that [latex]\large{5^{2n – 1}} + 1[/latex] is divisible by [latex]\large{6}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Basis step: show true for [latex]n=1[/latex].
[latex]\large{5^{2n – 1}} + 1 = {5^{2\left( 1 \right) – 1}} + 1[/latex]
[latex]\large = {5^{2 – 1}} + 1[/latex]
[latex]\large = {5^1} + 1[/latex]
[latex]\large = 5 + 1[/latex]
[latex]\large = 6[/latex]
Yes, it is divisible by [latex]6[/latex].
b) Assume true for [latex]n=k[/latex]. We have [latex]\large{5^{2k – 1}} + 1[/latex].
Write [latex]\large{5^{2k – 1}} + 1[/latex] in an equation expressing that it is divisible by [latex]6[/latex].
[latex]\large{5^{2k – 1}} + 1 = 6{\color{blue}x}[/latex]
for some integer [latex]x[/latex]
Solve for [latex]\large\color{red}{5^{2k}}[/latex].
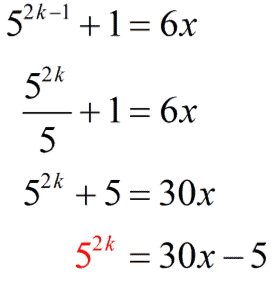
c) Prove the statement is true for [latex]n=k+1[/latex].
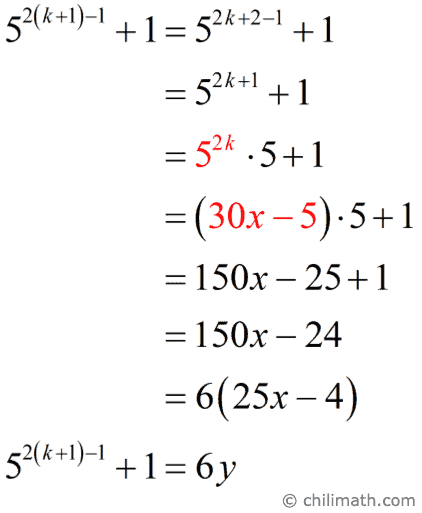
where [latex]y = 25x – 4[/latex]
Obviously [latex]y[/latex] is an integer since [latex]x[/latex] is also an integer
Clearly, [latex]\large{5^{2\left( {x + 1} \right) – 1}} + 1[/latex] is divisible by [latex]6[/latex].
[latex]\therefore[/latex] By the principle of mathematical induction, the statement is true for all positive integers.
Example 7: Use mathematical induction to prove that [latex]\large{9^n} – {2^n}[/latex] is divisible by [latex]\large{7}[/latex] for all positive integers [latex]\large{n}[/latex].
a) Show true for [latex]n=1[/latex].
[latex]\large{9^n} – {2^n} = {9^1} – {2^1}[/latex]
[latex]\large = 9 – 2[/latex]
[latex]\large = 7[/latex]
b) Assume true for [latex]n=k[/latex].
[latex]\large{9^n} – {2^n}[/latex] becomes [latex]\large{9^k} – {2^k}[/latex]
Write [latex]\large{9^k} – {2^k}[/latex] in equation expressing that it is divisible by [latex]\large{7}[/latex].
[latex]\large{9^k} – {2^k} = 7{\color{blue}x}[/latex]
for some positive integer [latex]\large{x}[/latex]
Solve for [latex]\large\color{red}{9^k}[/latex]:
[latex]\large{\color{red}{9^k}} = 7x + {2^k}[/latex]
c) Prove the statement is true for [latex]n=k+1[/latex].
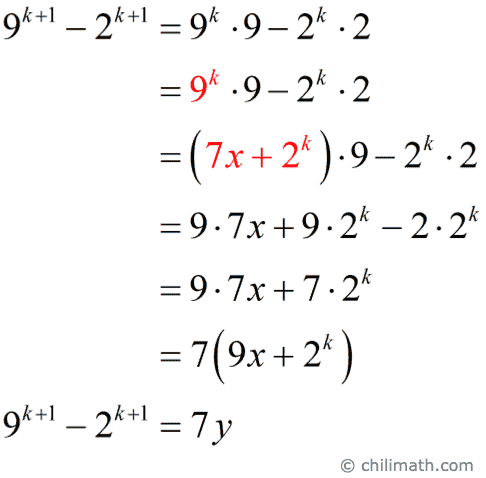
Since [latex]y[/latex] is an integer, thus [latex]\large{9^{k + 1}} – {2^{k + 1}}[/latex] is divisible by [latex]7[/latex].
[latex]\therefore[/latex] By the principle of mathematical induction, the statement is true for all positive integers.
You may also be interested in these related math lessons or tutorials:
