Solving Systems of Nonlinear Equations
A “system of equations” is a collection of two or more equations that are solved simultaneously. Previously, I have gone over a few examples showing how to solve a system of linear equations using substitution and elimination methods. It is considered a linear system because all the equations in the set are lines.
What is a Nonlinear System of Equations?
On the other hand, a nonlinear system is a collection of equations that may contain some equations of a line but not all of them. In this lesson, we will only deal with the system of nonlinear equations with two equations in two unknowns, [latex]x[/latex] and [latex]y[/latex].
There are seven (7) examples in this lesson.
Examples of How to Solve Systems of Nonlinear Equations
Example 1: Solve the system of nonlinear equations below.
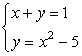
This system has two equations of each kind: linear and nonlinear. Start with the first equation since it is linear. You can solve for [latex]x[/latex] or [latex]y[/latex]. For this one, let’s solve for [latex]y[/latex] in terms of [latex]x[/latex].
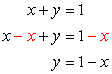
Substitute the value of [latex]y[/latex] into the second equation, and then solve for [latex]x[/latex]. In this problem, move everything to one side of the equation while keeping the opposite side equal to zero. After doing so, factor out the simple trinomial and then set each factor equal to zero to solve for [latex]x[/latex].
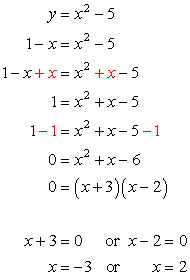
After solving the equation, we arrived at two values of [latex]x[/latex]. Substitute these numerical values to any of the two original equations. However, pick the “simpler” equation to simplify the calculation. Obviously, the linear equation [latex]x + y = 1[/latex] is the best choice!
- If [latex]x = – 3[/latex], solve for [latex]y[/latex].
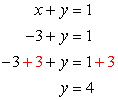
Answer: (– 3, 4)
- If [latex]x=2[/latex], solve for [latex]y[/latex].
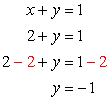
Answer: (2, –1)
Therefore, the solution set to the given system of nonlinear equations consists of two points which are (– 3, 4) and (2, –1).
Graphically, we can think of the solution to the system as the points of intersections between the linear function [latex]\color{red}x + y = 1[/latex] and quadratic function [latex]\color{blue}y = {x^2} – 5[/latex].
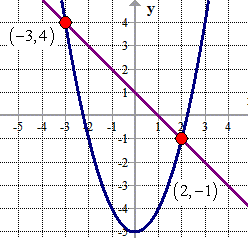
Example 2: Solve the system of equations below.
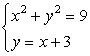
The first equation is a circle with a radius of [latex]3[/latex] since the general formula of a circle is [latex]{x^2} + {y^2} = {r^2}[/latex].
What I will do is to substitute the expression of [latex]y[/latex] which is [latex]\color{blue}x+3[/latex] from the bottom equation to the [latex]y[/latex] of the top equation. Then we should be able to solve for [latex]x[/latex].
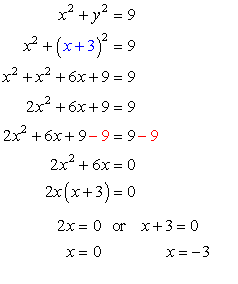
Use these values of [latex]x[/latex] to find the corresponding values of [latex]y[/latex]. I would pick the simpler equation (bottom equation) [latex]y=x+3[/latex] to solve for [latex]y[/latex].
- If [latex]x=0[/latex], solve for [latex]y[/latex].
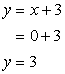
Answer: (0, 3)
- If [latex]x = – 3[/latex], solve for [latex]y[/latex].
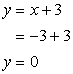
Answer: (– 3, 0)
The final answers are the points (0, 3) and (– 3, 0). These are the points of intersections of the given line and circle centered at the origin.
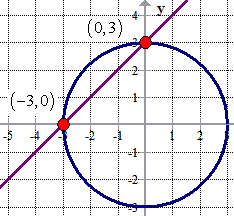
Example 3: Solve the system of equations below.
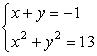
This problem is very similar to problem #2. We have a line (top equation) intersecting a circle (bottom equation) at two points.
Step 1: Solve the top equation for [latex]y[/latex].
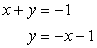
Step 2: Plug the value of [latex]y[/latex] into the bottom equation. You will be required to square a binomial, combine like terms and factor out a trinomial to get the values of [latex]x[/latex]. Here is the solution:
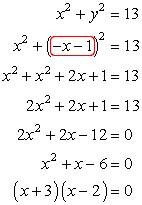
Therefore, the values of [latex]x[/latex] are
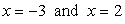
Step 3: Back substitute these [latex]x{\rm{ – values}}[/latex] into the top equation [latex]x + y = – 1[/latex] to get the corresponding [latex]y{\rm{ – values}}[/latex].
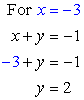
Answer: (– 3, 2)
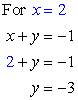
Answer: (2, – 3)
Step 4: Here is the graph of the line intersecting the circle at (– 3, 2) and (2, – 3).
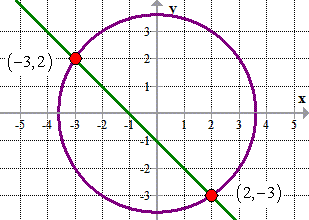
Example 4: Solve the system of nonlinear equations
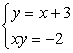
Substitute the expression of [latex]y[/latex] from the top equation to the [latex]y[/latex] of the bottom equation. Apply the distributive property, then move everything to the left. Factor out the trinomial, then set each factor equal to zero to solve for [latex]x[/latex].
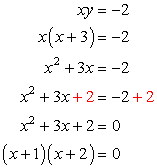
So we have,
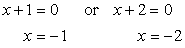
Since we now have the values of [latex]x[/latex], pick any of the original equations to solve for [latex]y[/latex]. The obvious choice is [latex]y=x+3[/latex] because it is much simpler than the other one.
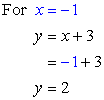
Answer: (–1, 2)
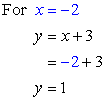
Answer: (– 2, 1)
The graph shows the intersection of the oblique hyperbola and the line at points (–1, 2) and (– 2, 1).
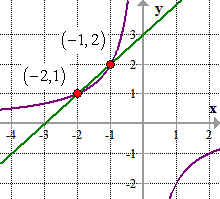
Example 5: Solve the system of nonlinear equations
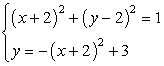
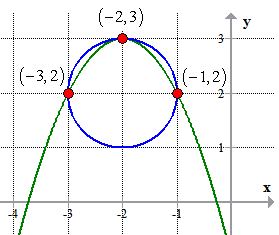
Observe that the first equation is of a circle centered at [latex](-2, 2)[/latex] with a radius of [latex]1[/latex]. The second equation is a parabola in standard form with vertex at [latex](-2, 3)[/latex]. We expect that the solutions to this system of nonlinear equations are the points where the parabola (quadratic function) intersects the given circle.
We will solve this in two ways. First by the substitution method then followed by the elimination method.
I. Using the Substitution Method
It would be tempting to just substitute the value of [latex]y[/latex] from the bottom equation to the top equation. You may try it. But you should immediately realize that it makes the problem more complicated to work on. There’s a better way, though.
Isolate the term [latex]{\left( {x + 2} \right)^2}[/latex] of the second equation and plug it into the first equation.
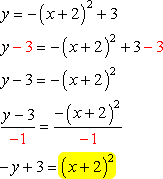
Next, substitute this into the second equation, which gives us an equation with a single variable just in [latex]y[/latex].
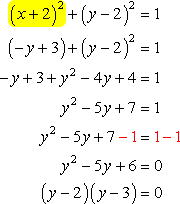
Setting each factor equal to zero and solving for [latex]y[/latex], we get
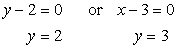
Now, we want to find the corresponding values of [latex]x[/latex] when [latex]y=2[/latex] and [latex]y=3[/latex]. I will use the equation of a circle to do just that.
- If [latex]y=2[/latex], solve for [latex]x[/latex].
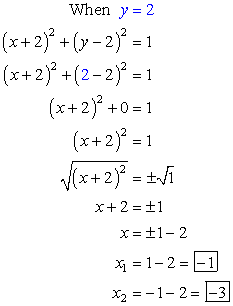
Answer: (–1, 2) and (– 3, 2)
- If [latex]y=3[/latex], solve for [latex]x[/latex].
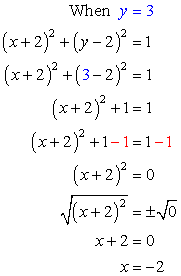
Answer: (– 2, 3)
Therefore, the complete solutions are the points of intersections of a quadratic function and a circle at (–1, 2), (– 3, 2) and (– 2, 3).
II. Using the Elimination Method
To solve by elimination method, keep all the terms with [latex]x[/latex] and [latex]y[/latex] on the left side and move the constant to the right. Make sure that you align similar terms. In this case, only the terms with [latex]{\left( {x + 2} \right)^2}[/latex] and the constants should have similar terms.
Then subtract the top equation by the bottom equation. Don’t forget to switch the signs when you subtract, i.e., positive turns into negative, and vice versa. The term [latex]{\left( {x + 2} \right)^2}[/latex] should be eliminated after subtraction.
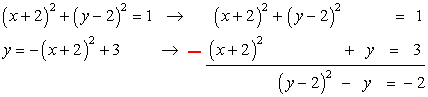
Since the [latex]\color{red}{\left( {x + 2} \right)^2}[/latex] term is gone, we are left with a simple quadratic equation with variable [latex]y[/latex] only then can be solved using factoring.
Start by expanding the binomial term, combine like terms, move everything to the left, factor the resulting trinomial, and set each factor equal to zero to solve for [latex]y[/latex].
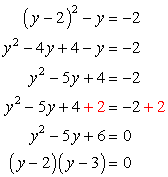
Setting each factor equal to zero and solving for [latex]y[/latex], we get
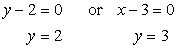
Notice that we arrived at the same values of [latex]y[/latex] using the substitution method as shown above. From this point, the solution is now the same as shown above that’s why I will not show the rest of it.
The solution set consists of the points of intersections: (–1, 2), (– 3, 2) and (– 2, 3).
Example 6: Solve the following system
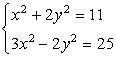
Since the [latex]y^2[/latex] terms have the same coefficient but opposite in signs, we can add the two equations together to eliminate the variable [latex]y[/latex]. This should leave us with a simple quadratic equation that can be solved easily using the square root method.
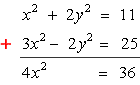
Next, divide both sides of the equation by the coefficient of the [latex]x^2[/latex] term, followed by applying the square root on both sides to get the values of [latex]x[/latex]. Don’t forget to attach the plus or minus symbol whenever you get the square root of something.
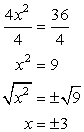
Pick any of the two original equations, and find the values of [latex]y[/latex] when [latex]\color{blue}x = \pm\, 3[/latex]. I will use the first equation because it is much simpler!
- If [latex]x=3[/latex], solve for [latex]y[/latex].
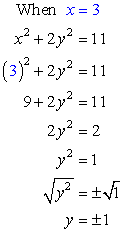
Answer: (3, 1) and (3, –1)
- If [latex]x=-3[/latex], solve for [latex]y[/latex].
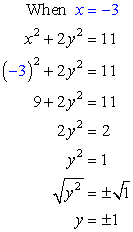
Answer: (– 3, 1) and (– 3, –1)
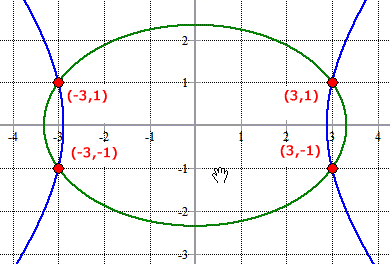
The solutions to this system of nonlinear equations consist of the four points of intersections:
(3, 1), (3, –1), (– 3, 1) and (– 3, –1)
In fact, these are the points of intersections of the given ellipse (first equation) and hyperbola (second equation).
Graphically, it looks like the one below.
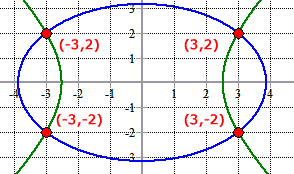
Example 7: Solve the following system
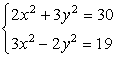
We will also solve this using the elimination method. However, multiply both of the equations first by some number so that their constants become the same but opposite in signs.
Eliminate [latex]y^2[/latex] by multiplying the first equation by [latex]2[/latex], and the second equation by [latex]3[/latex], and finally adding them together!
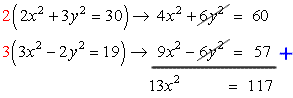
Now, solve for [latex]x[/latex] by dividing both sides by the coefficient of the [latex]x^2[/latex] term, and then performing the square root operation on both sides of the equation.
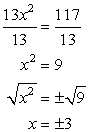
Back substitute the values of [latex]x[/latex] into any of the original equations to solve for [latex]y[/latex]. Let’s use the first equation.
- If [latex]x=3[/latex], solve for [latex]y[/latex].
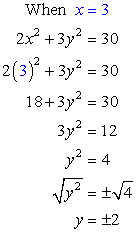
Answer: (3, 2) and (3, – 2)
- If [latex]x=-3[/latex], solve for [latex]y[/latex].
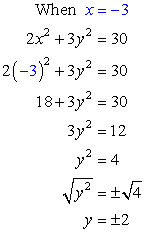
Answer: (– 3, 2) and (– 3, – 2)
The solutions to this nonlinear system are the points of intersections of the given ellipse and hyperbola.