Proofs of Logarithm Properties or Rules

The logarithm properties or rules are derived using the laws of exponents. That’s the reason why we are going to use the exponent rules to prove the logarithm properties below.

Most of the time, we are just told to remember or memorize these logarithmic properties because they are useful. But in this lesson, we are going to provide justifications or simple proofs why they are true.

---

It is true that a logarithmic equation can be expressed as an exponential equation, and vice versa. In other words, logarithms and exponentials are equivalent.

I. Conditional Statement

First, consider the conditional statement “if [latex]{\log _b}x = y[/latex], then [latex]x = {b^y}[/latex].” We can also write the statement symbolically to denote implication using the rightward arrow, →. This conditional statement is true by definition.

[latex]\Large{\log _b}{\color{blue}x} = {\color{red}y} \,\,\to \,\,{\color{blue}x} = {b^{\color{red}y}}[/latex]

Examples:

1. [latex]{\log _2}32 = 5 \,\,\to\,\, 32 = {2^5}[/latex]

2. [latex]{\log _5}\left( {\large{{{1 \over {25}}}}} \right) = – 2\,\, \to\,\, {\large{{1 \over {25}}}} = {5^{ – 2}}[/latex]

3. [latex]{\log _3}1 = 0 \,\,\to\,\, 1 = {3^0}[/latex]

---

II. Converse of the Conditional Statement

The converse of the original statement is true as well by definition, that is, “if [latex]x = {b^y}[/latex], then [latex]{\log _b}x=y[/latex].” We can also write it symbolically as:

[latex]\Large{\color{blue}x} = {b^{\color{red}y}} \,\,\to \,\,{\log _b}{\color{blue}x} = {\color{red}y}[/latex]

Examples:

1. [latex]81 = {3^4} \,\,\to\,\, {\log _3}81 = 4[/latex]

2. [latex]{\Large{{1 \over 8}}} = {2^{ – 3}} \,\,\to\,\, {\log _2}\left( {\Large{{{1 \over 8}}}} \right) = – 3[/latex]

3. [latex]16 = {64^{\small{{{2 \over 3}}}}} \,\,\to\,\, {\log _{64}}16 = {\Large{{2 \over 3}}}[/latex]

---

III. Biconditional Statement

Since the conditional statement and its converse are both true, they are a biconditional statement. We use “if and only if” or the double-headed arrow, ⟷, to denote a biconditional statement. Thus, “[latex]{\log _b}x = y[/latex] if and only if [latex]x = {b^y}[/latex].” Writing it symbolically, we have:

[latex]\Large{\log _b}{\color{blue}x} = {\color{red}y} \,\,\leftrightarrow\,\,{\color{blue}x} = {b^{\color{red}y}}[/latex]

This means essentially that there is an equivalence between logarithmic statements and exponential statements.

Thus, given a logarithmic statement, we can express it as an exponential statement. In the same manner, if we have an exponential statement, we can transform it into a logarithmic statement.

Now, let’s get started proving the four (4) logarithm properties or rules.

---

Proof of the Product Property of Logarithm

[latex]\large{\log _b}\left( {{x \cdot y}} \right) = {\log _b}x + {\log _b}y[/latex]

Step 1: Let [latex]{\color{red}m }= {\log _b}x[/latex] and [latex]{\color{blue}n} = {\log _b}y[/latex].

Step 2: Transform each logarithmic equation to its equivalent exponential equation.

[latex]\large{m = {\log _b}x \,\,\to x\,\, = {b^m}}[/latex]

[latex]\large{n = {\log _b}y \to y = {b^n}}[/latex]

Step 3: Since we are proving the product property, we will multiply [latex]x[/latex] by [latex]y[/latex]. Simplify by applying the product rule of exponent. That is, copy the common base then add the exponents.

[latex]\large{xy = \left( {{b^m}} \right)\left( {{b^n}} \right)}[/latex]

[latex]\large{xy = {b^{\,m + n}}}[/latex]

Step 4: Take the logarithms of both sides of the equation. Focus your attention on the right side of the equation. Simplify it using the Logarithm of a Base to a Power Rule. I placed the rule below for your convenience.

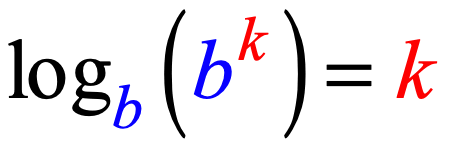
[latex]\large{{\log _b}\left( {xy} \right) = {\log _b}\left( {{b^{m + n}}} \right)}[/latex]

[latex]\large{{\log _b}\left( {xy} \right) = m + n}[/latex]

Step 5: Finally, substitute back the expressions for [latex]\color{red}m[/latex] and [latex]\color{blue}{n}[/latex] that we assigned in Step 1.

[latex]\large{{\log _b}\left( {xy} \right) = {\log _b}x + {\log _b}y}[/latex]

or

[latex]\large{{\log _b}\left( {x \cdot y} \right) = {\log _b}x + {\log _b}y}[/latex]

---

Proof of the Quotient Property of Logarithm

[latex]\large{{\log _b}\left( {\Large{{{x \over y}}}} \right) = {\log _b}x – {\log _b}y}[/latex]

Step 1: Assume that [latex]{\color{red}m }= {\log _b}x[/latex] and [latex]{\color{blue}n} = {\log _b}y[/latex].

Step 2: Express each logarithmic equation as an exponential equation.

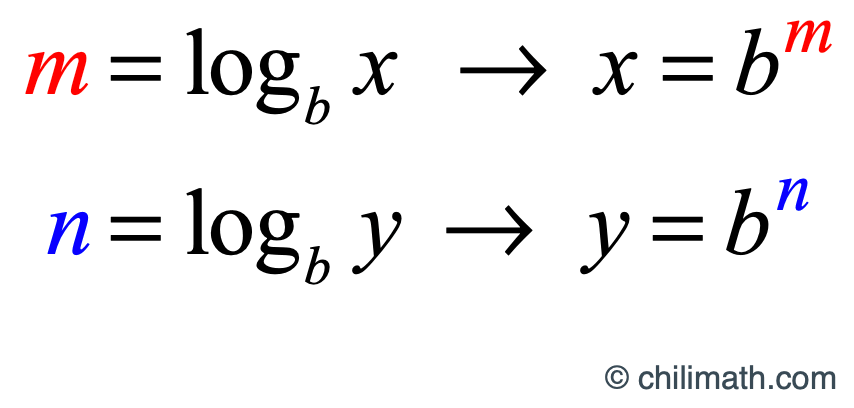
Step 3: We want to prove the Quotient Rule of Logarithm so we will divide [latex]x[/latex] by [latex]y[/latex], therefore our set-up is [latex]\Large{x \over y}[/latex]. Remember when dividing exponents, you copy the common base then subtract the exponent of the numerator by the exponent of the denominator.

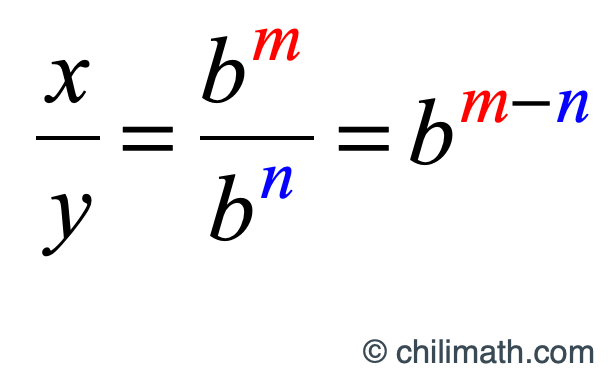
That means, we get:

[latex]\Large{{\LARGE{{x \over y}}} = {b^{\,m – n}}}[/latex]

Step 4: Take the logarithm with base [latex]\color{green}\large{b}[/latex] of both sides of the equation. The choice of base [latex]\color{green}\large{b}[/latex] is intentional because we want to get rid of the base [latex]\large{b}[/latex] on the right side of the equation.

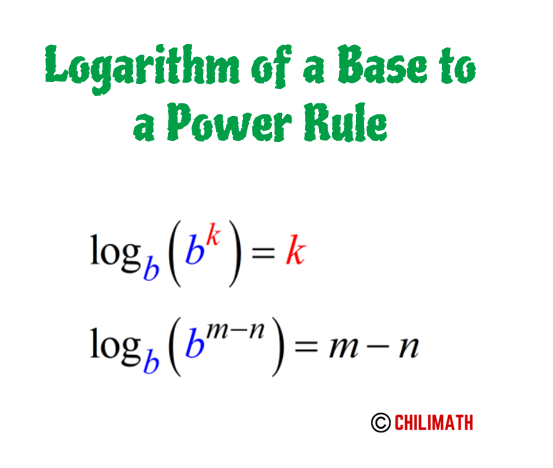
Therefore, we have:

[latex]{\log _b}\left( {{\Large{{x \over y}}}} \right) = {\log _b}\left( {{b^{\,m – n}}} \right)[/latex]

[latex]{\log _b}\left( {{\Large{{x \over y}}}} \right) = m – n[/latex]

Step 5: Since we assume in our first step that [latex]{\color{red}m }= {\log _b}x[/latex] and [latex]{\color{blue}n} = {\log _b}y[/latex], we replace [latex]m[/latex] and [latex]n[/latex] by their corresponding log expressions. This results to the Quotient Property of Logarithm as intended.

[latex]{\log _b}\left({ \Large{{{x \over y}}}} \right) = {\log _b}x – {\log _b}y[/latex]

---

Proof of the Power Property of Logarithm

[latex]\large{\log _b}\left( {{x^k}} \right) = k \cdot {\log _b}x[/latex]

Step 1: Suppose [latex]\large{{\color{red}m} = {\log _b}x}[/latex].

Step 2: Rewrite [latex]\large{{\color{red}m} = {\log _b}x}[/latex] as an exponential equation. Use the rule below when transforming log equation into an exponential equation.

[latex]\Large{m = {\log _b}x \to x = {b^m}}[/latex]

Step 3: Raise both sides of the equation to the [latex]\large{k}[/latex] power.

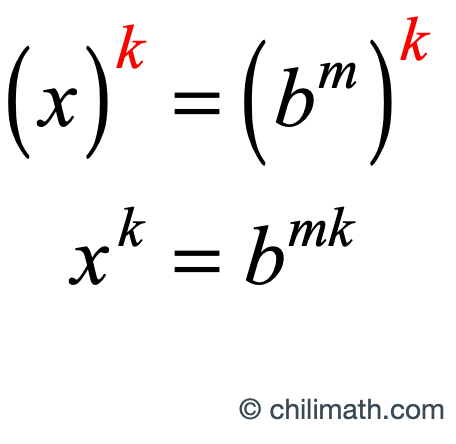
Step 4: Perform logarithms with base [latex]b[/latex] to both sides of the equation then simplify.

Use this handy rule [latex]\large{\log _b}{b^x} = x[/latex] to simplify the right-hand side of the equation.

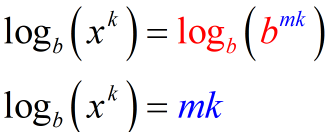
Step 5: In step 1, we suppose [latex]\large{{\color{red}m} = {\log _b}x}[/latex]. The final step is to substitute the expression of [latex]m[/latex] as logs into the right side of the equation.

[latex]\large{{\log _b}\left( {{x^k}} \right) = mk}[/latex]

[latex]\large{{\log _b}\left( {{x^k}} \right) = \left( {{{\log }_b}x} \right)k}[/latex]

We just need to clean up the right side of the equation by putting the variable [latex]k[/latex] in front of the log expression. And we are done!

[latex]\large{\log _b}\left( {{x^k}} \right) = k \cdot {\log _b}x[/latex]

---

The Change-of-Base Property of Logarithm

[latex]\Large{{\log _a}x = {{{{\log }_b}x} \over {{{\log }_b}a}}}[/latex]

Step 1: Let [latex]{\color{red}k} = {\log _a}x[/latex].

Step 2: Express [latex]{\color{red}k} = {\log _a}x[/latex] as an exponential equation.

[latex]\large{k = {\log _a}x \,\,\to\,\, x = {a^k}}[/latex]

Step 3: Take the logarithms with a different base of both sides of the exponential equation, [latex]x = {a^k}[/latex].

The choice of the base doesn’t matter as long as the base is greater than zero but doesn’t equal [latex]1[/latex]. As you can see below, I use different bases for emphasis which are [latex]b[/latex], [latex]c[/latex], [latex]d[/latex], and [latex]f[/latex].

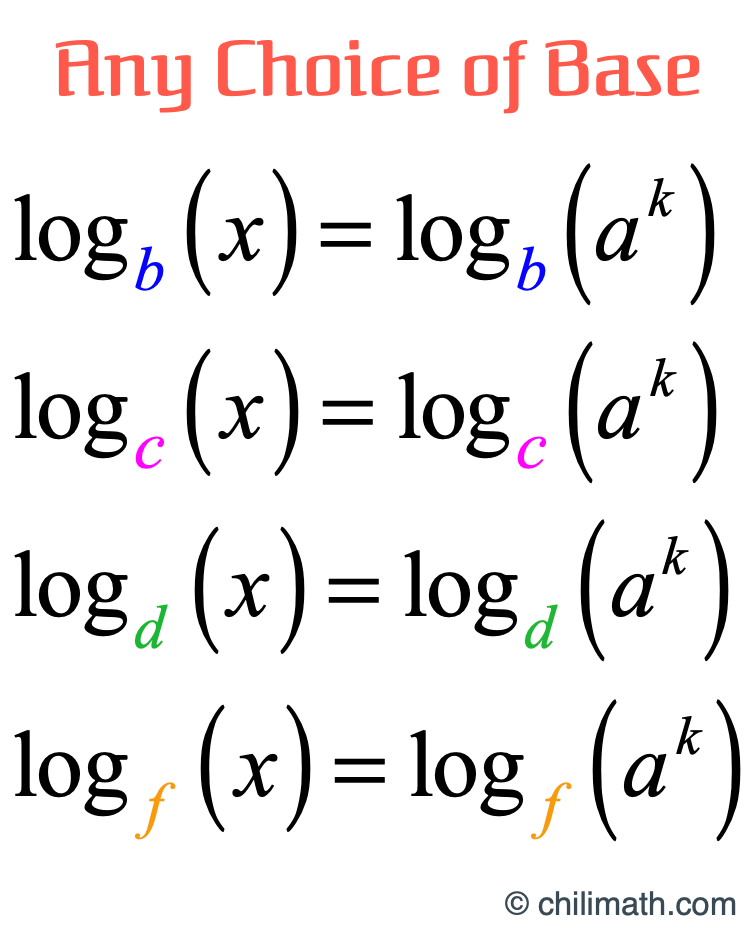
For simplicity’s sake, we will use the first one on the list which is [latex]\large{{\log _{{\large{\color{blue}b}}}}}[/latex].

[latex]\large{{\log _b}\left( x \right) = {\log _b}\left( {{a^{\large{{\color{red}k}}}}} \right)}[/latex]

Step 4: Now, apply the Power Rule of Logarithm on the right side of the exponential equation to bring down the exponent [latex]k[/latex]. Then solve for [latex]k[/latex] by dividing both sides of the equation by [latex]{\log _b}\left( a \right)[/latex].

[latex]\large{{\log _b}\left( x \right) = {\color{red}k} \cdot {\log _b}\left( a \right)}[/latex]

[latex]\Large{{{{{\log }_b}\left( x \right)} \over {{{\log }_b}\left( a \right)}} = {{{\color{red}k} \cdot {{\log }_b}\left( a \right)} \over {{{\log }_b}\left( a \right)}}}[/latex]

[latex]{\Large{{{{{\log }_b}\left( x \right)} \over {{{\log }_b}\left( a \right)}}}} = {\color{red}k}[/latex]

Step 5: Our last step is to substitute back the expression for [latex]k = {\log _a}x[/latex]. We established it in Step 1.

[latex]{\Large{{{{{\log }_b}\left( x \right)} \over {{{\log }_b}\left( a \right)}}}} = {\color{red}k}[/latex]

[latex]{\Large{{{{{\log }_b}\left( x \right)} \over {{{\log }_b}\left( a \right)}}}} = {\log _a}x[/latex]

or

[latex] {\log _a}x={\Large{{{{{\log }_b}\left( x \right)} \over {{{\log }_b}\left( a \right)}}}}[/latex]

---

You may also be interested in these related math lessons or tutorials:

Logarithm Rules