Law of Sines

To solve the unknown sides and angles of oblique triangles, we will need the Law of Sines or Sine Rule. By the way, an oblique triangle is a type of triangle which does not contain a right angle or a 90-degree angle.

The Law of Sines can be summarized as:

Given that [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex] are the angle measures of a triangle and [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are their corresponding side lengths, then for triangle ABC

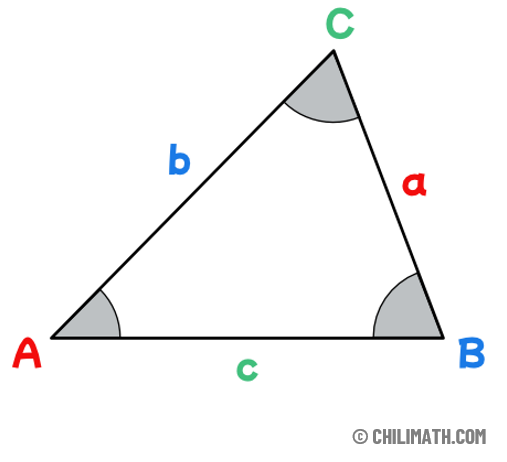
we have the relationship,

[latex]\Large{{\sin A} \over a} = {{\sin B} \over b} = {{\sin C} \over c}[/latex]

In other words, the ratio of the sine of an angle in a triangle to its opposite side is the same as the ratios of the sines of the other two angles to their opposite sides. That is, the ratio of the sine of an angle to its opposite side is the same in every triangle.

That is to say, the ratios between all the angles and their opposite side lengths are directly proportional to each other.

But of course, we can also flip over the equation and it would still work!

[latex]\Large{a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}}[/latex]

---

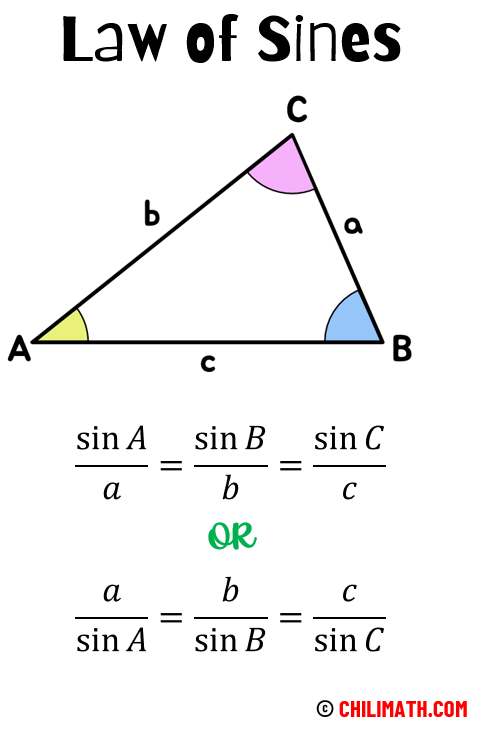
In plain words, it means

---

When solving problems using the Law of Sines, there are usually three (3) cases that we are going to deal with.

But the general idea is that if any two angles and one side of an oblique triangle are given then it can easily be solved by the Law of Sines.

Case 1: Solving an SAA (Side-Angle-Angle) Triangle

In an SAA Triangle, we are given two angles of a triangle and a side opposite to one of the angles (non-included side). This case in particular is the easy type because we are given one of the three ratios – that is, one angle and an opposite side.

Case 2: Solving an ASA (Angle-Side-Angle) Triangle

In an ASA Triangle, we are given two angles of a triangle and an included side. In this case, we don’t have a ratio of an angle and an opposite side just yet. But we can find the third angle with an opposite side by using the fact that the sum of all the angles of a triangle is [latex]{180^\circ }[/latex].

Case 3: Solving an SSA (Side-Side-Angle) Triangle

In a SSA Triangle, we are given two sides of a triangle and an angle that is opposite to one of the sides. This case is known as the ambiguous case because there may be no triangle at all, one triangle or two triangles.

---

Examples of Solving Law of Sines Problems

Part I: SAA (Side-Angle-Angle) Triangle (non-included side)

Example 1: In [latex]\triangle[/latex] [latex]ABC[/latex], [latex]A=60^\circ[/latex], [latex]C=82^\circ[/latex], and [latex]a=24[/latex]. Solve the triangle.

The first thing we have to do is to draw a rough sketch of the triangle. The drawing does not need to be perfect but just enough for us to see the big picture.

Here’s triangle [latex]ABC[/latex] with the measurements provided to us. Make sure that you place the measure of side [latex]a[/latex] opposite angle [latex]A[/latex]. That is, side length [latex]24[/latex] is opposite [latex]60^\circ[/latex].

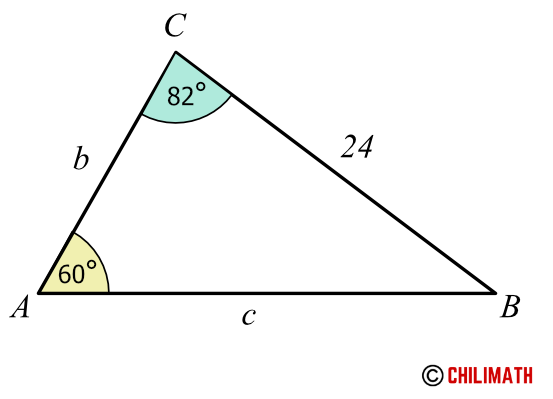
The problem is asking us to solve the triangle. What it means is that we are going to find the values or measurements of the remaining angle and sides. In this case, we want to find the measure of angle [latex]B[/latex] and side lengths [latex]b[/latex] and [latex]c[/latex].

Since we are given two angles and a side (non-included), this is called the SAA (Side-Angle-Angle) case. This is in fact the easiest case because we are given with one of the three ratios. Notice, [latex]\angle A[/latex] and its opposite side [latex]a[/latex] represent a ratio.

Having said all that, we are now ready to solve the triangle in question.

Let’s begin by determining angle [latex]\angle B[/latex]. We don’t need to use the Law of Sines here. We will simply use the fact that the sum of the internal angles of a triangle is always [latex]180^\circ[/latex]. Since we know the measures of angle [latex]\angle A[/latex] and angle [latex]\angle C[/latex], we can set up the equation to solve for angle [latex]\angle B[/latex] as:

[latex]\angle A + {\color{red}\angle B} + \angle C = 180^\circ[/latex]

Isolating [latex]\angle B[/latex] on the left side of the equation by subtracting both sides of the equation by [latex]\angle A[/latex] and [latex]\angle C[/latex], we obtain

[latex]{\color{red}\angle B} = 180^\circ – \angle A – \angle C[/latex]

That means, the measure of [latex]\angle B[/latex] is

[latex]{\color{red}\angle B} = 180^\circ – 60^\circ – 82^\circ = 38^\circ[/latex]

Next, we will find side [latex]c[/latex]. The key is to utilize the known ratio which in this case is for side [latex]a[/latex] and angle [latex]A[/latex], [latex]\large {a \over {\sin A}}[/latex]. Because we are solving for side [latex]c[/latex] that means we must use angle [latex]C[/latex]. So this is how the equation would look like.

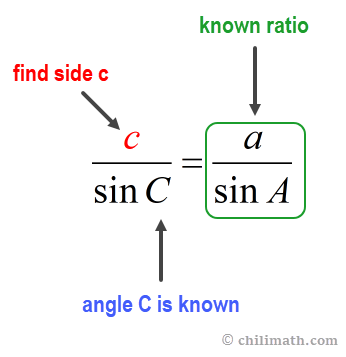
Since [latex]C=82^\circ[/latex], [latex]a=24[/latex], and [latex]A=60^\circ[/latex], here’s the equation that we will use to solve for side [latex]c[/latex].

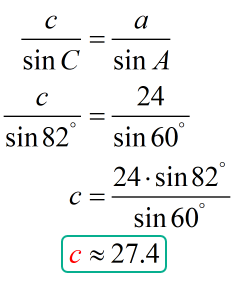
Finally, we will solve for side [latex]b[/latex]. Remember that we calculated the measure of angle [latex]\angle B[/latex] above. Together with the known ratio of side [latex]a[/latex] and angle [latex]\angle A[/latex], we can set up an equation to solve for side [latex]b[/latex].

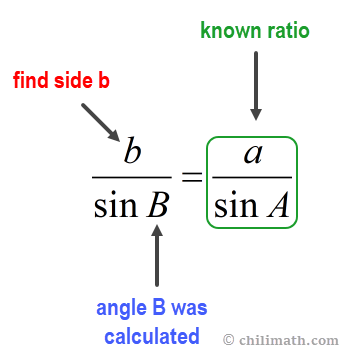
Since [latex]B=38^\circ[/latex], [latex]a=24[/latex], and [latex]A=60^\circ[/latex], here’s the equation that we will use to solve for side [latex]b[/latex].

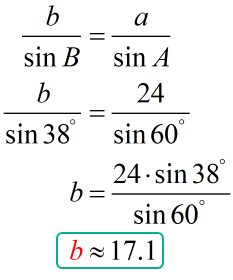
Therefore, the final solution is [latex]B=38^\circ[/latex], [latex]b \approx 17.1[/latex], and [latex]c \approx 27.4[/latex].

---

Example 2: In [latex]\triangle[/latex] [latex]ABC[/latex], [latex]A=33^\circ[/latex], [latex]B=41^\circ[/latex], and [latex]b=53[/latex]. Solve the triangle.

Let’s do an example similar to example #1. This is also an SAA case because we are given two angles and a non-included side. Remember, this is the easiest case because a ratio is immediately provided to us that means we can set up an equation to solve the triangle right off the bat.

Below is the rough sketch of the triangle in question. Notice angle [latex]\angle B[/latex] with a measure of [latex]41^\circ[/latex] is opposite side [latex]b[/latex] with side length of [latex]53[/latex]. Since we don’t know the measures of sides [latex]a[/latex] and [latex]c[/latex], and angle [latex]\angle C[/latex], we just label them accordingly.

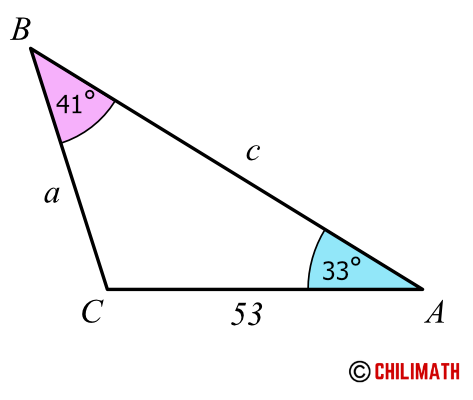
Because the measures of angle [latex]\angle B[/latex] and side [latex]b[/latex] are given, they become the known ratio in the equation, that is, [latex]\large {b \over {\sin B}}[/latex] or [latex]\large {{\sin B}\over b}[/latex]. We will use this ratio to solve the other sides namely sides [latex]a[/latex] and [latex]c[/latex].

But before we even find the sides, the most obvious and logical step is to find the third angle of the triangle because we already know the other two.

To solve for angle [latex]\angle C[/latex], we simply subtract the measures of [latex]\angle A[/latex] and [latex]\angle B[/latex] from [latex]180^\circ[/latex].

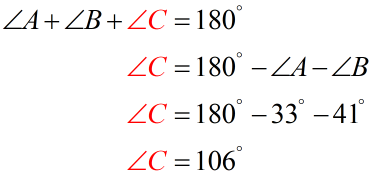
Now, let’s calculate side [latex]a[/latex].

Lastly, we compute side [latex]c[/latex].

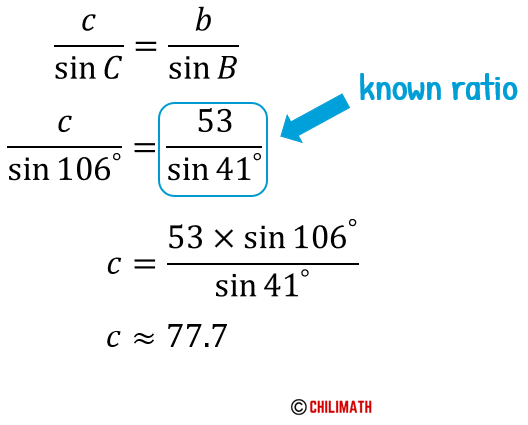
Therefore, the final solution is [latex]C=106^\circ[/latex], [latex]c \approx 77.7[/latex], and [latex]a \approx 44.0[/latex].

---

Part II: ASA (Angle-Side-Angle) Triangle (with included side)

Example 3: In [latex]\triangle[/latex] [latex]ABC[/latex], [latex]A=74^\circ[/latex], [latex]B=50^\circ[/latex], and [latex]c=75[/latex]. Solve the triangle.

The very first thing we should do is to draw a representation of the given triangle. Again, it doesn’t have to be perfect but just enough to see what’s going on.

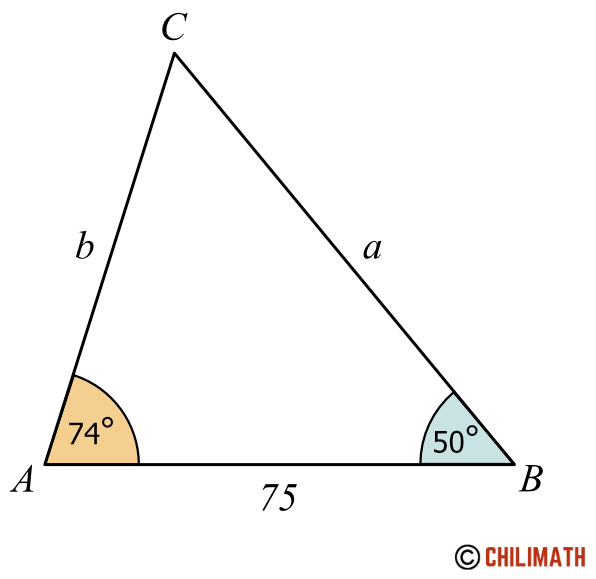
Notice that upon drawing the triangle, we see that side [latex]c[/latex] is between angles [latex]\angle A[/latex] and [latex]\angle B[/latex]. This is indeed a case of ASA ( Angle-Side-Angle) because we have an included side.

Let’s study the illustration further. Observe that the sides opposite angles [latex]\angle A[/latex] and [latex]\angle B[/latex] are not known which means they are not prime candidates for usable ratios for the Sine Rule equations.

What else? The measure of side [latex]c[/latex] is known but angle [latex]\angle C[/latex] is not. However, the value of angle [latex]\angle C[/latex] can easily be found! Since the measures of the other two angles of the triangle are known, namely angles [latex]\angle A[/latex] and [latex]\angle B[/latex], we can use the idea that the sum of the internal angles of a triangle is [latex]{180^\circ }[/latex] and therefore the measure of angle [latex]\angle C[/latex] is easily calculated. After finding [latex]\angle C[/latex] and together with side [latex]c[/latex], we will have a known ratio that we can use to find the other sides [latex]a[/latex] and [latex]b[/latex].

Let’s find the measure of angle [latex]\angle C[/latex].

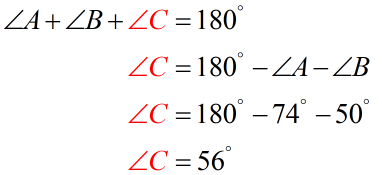
It means our known ratio which we can use in the equation to solve the other two sides is

Because we have a known ratio, we are ready to start solving the measures of the remaining sides. Let’s start with side [latex]a[/latex].

To solve for side side [latex]a[/latex]:

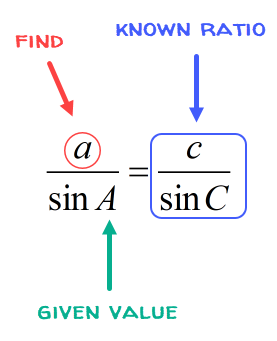
Substitute the value of the known ratio [latex]\large {{75} \over {\sin {{56}^\circ }}}[/latex] and angle [latex]A[/latex] which equals [latex]{74^\circ }[/latex] into the Sine Laws’ equation to solve for side [latex]a[/latex].

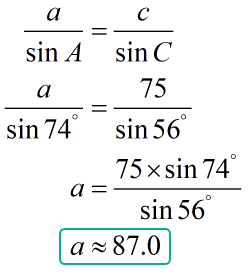
To solve for side [latex]b[/latex]:

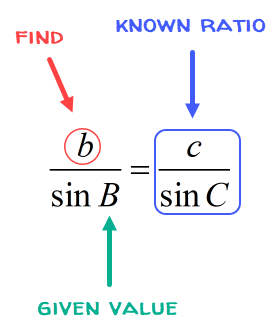
In the same manner, plug in the value of the known ratio [latex]\large {{75} \over {\sin {{56}^\circ }}}[/latex] and angle [latex]B[/latex] which equals [latex]{50^\circ }[/latex] into the Sine Laws’ equation to solve for side [latex]b[/latex].

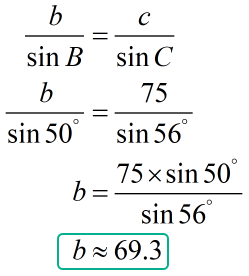
Therefore, the final solution is [latex]C=56^\circ[/latex], [latex]a \approx 87.0[/latex], and [latex]b \approx 69.3[/latex].

---

Example 4: In [latex]\triangle[/latex] [latex]ABC[/latex], [latex]B=125^\circ[/latex], [latex]C=25^\circ[/latex], and [latex]a=102[/latex]. Solve the triangle.

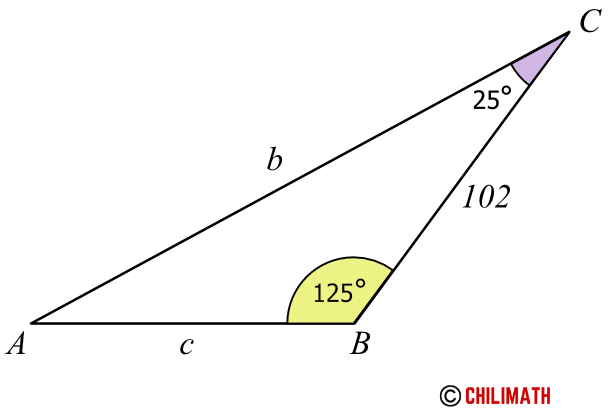
Let’s do another example on ASA ( Angle-Side-Angle) triangle for more practice! The first step is to find the missing third angle of the triangle. Since the internal angles of a triangle add up to [latex]180^\circ[/latex], we can set up the equation below to solve for angle [latex]\angle A[/latex].

Find angle [latex]\angle A[/latex]:

Set the sum of angles [latex]\angle A[/latex], [latex]\angle B[/latex], and [latex]\angle C[/latex] equal to [latex]180^\circ[/latex]. Then subtract both sides of the equation with the measures of angles [latex]\angle B[/latex] and [latex]\angle C[/latex] to get the value of angle [latex]\angle A[/latex].

Now, we have a known ratio to use in the Sine Rule equation which is angle [latex]\angle A[/latex] and side [latex]a[/latex] which is given to us.

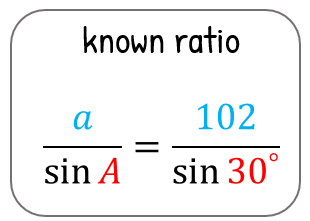
By having a known ratio, we are ready to solve for the other two sides of the triangle namely sides [latex]b[/latex] and [latex]c[/latex].

To solve for side [latex]b[/latex]:

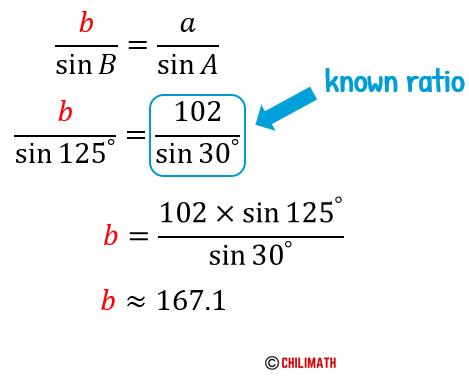
Finally, let’s solve for side [latex]c[/latex]:

Therefore, the final solution is [latex]A=30^\circ[/latex], [latex]b \approx 167.1[/latex], and [latex]c \approx 86.2[/latex].

---

Part III: SSA (Side-Side-Angle) Triangle (angle opposite to one of the sides)

Note that in our previous examples, we are given two angles and one side which determines a unique triangle. That’s why it is easier to solve. But if we are given two sides and an angle, it’s a very different story because three (3) possible scenarios can happen. For this reason, Side-Side-Angle (SSA) is called the Ambiguous case.

---

Case 1: SSA Ambiguous Case – No Triangle

If angle [latex]A[/latex] is acute and side [latex]a[/latex] is less than the height of the triangle, that is, [latex]a < h[/latex], then no triangle exists.

---

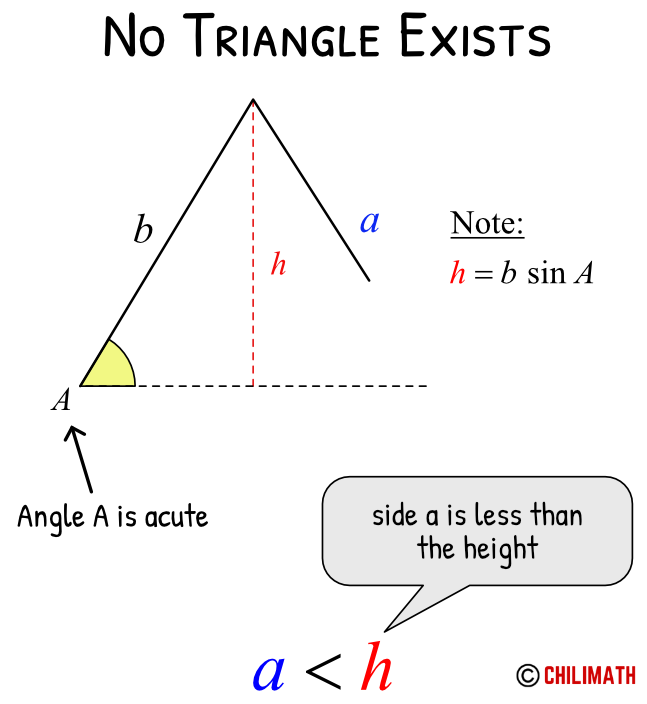
If angle [latex]A[/latex] is obtuse and side [latex]a[/latex] is less than or equal to side [latex]b[/latex], that is, [latex]a \le b[/latex], then no triangle exists.

---

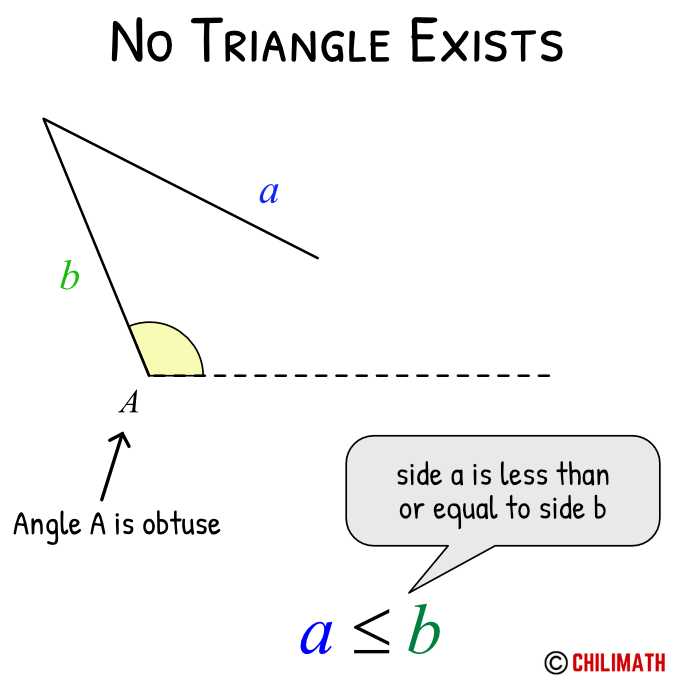
Let’s use this knowledge in the following examples.

Example 5: Solve triangle [latex]\triangle[/latex] [latex]ABC[/latex] if [latex]A=73^\circ[/latex], [latex]a=41[/latex], and [latex]b=52[/latex].

It’s a good practice to always draw a rough sketch of the triangle in question so that we know what we are dealing with. It doesn’t need to be perfect. The goal is to see the big picture.

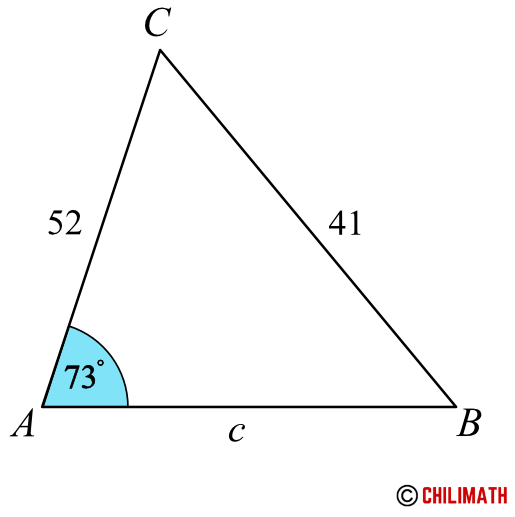
This is obviously a case of SSA triangle because we are given two sides and a non-included angle. This means that we are dealing with an ambiguous case which means we need to be a bit careful.

Since angle [latex]A[/latex] is an acute angle, we want to compare the height of the triangle and the length of side [latex]a[/latex]. If side [latex]a[/latex] is less than the height, [latex]a<h[/latex], it implies that side [latex]a[/latex] is not long enough to form a triangle thus no triangle exists.

Let’s redraw the figure with the height included for emphasis.

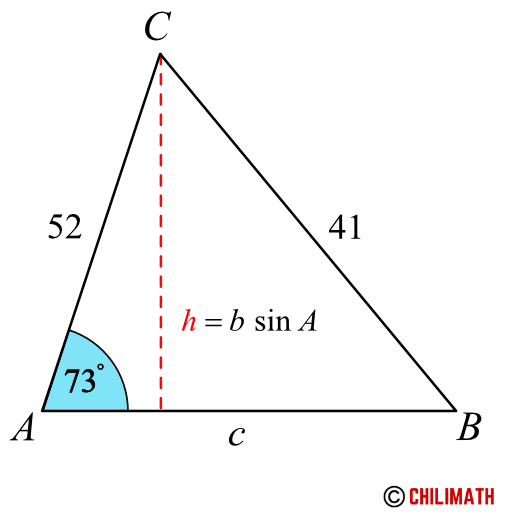
Remember, to find the height, [latex]h[/latex], we need the sine function because it is the ratio of the opposite side and the hypotenuse.

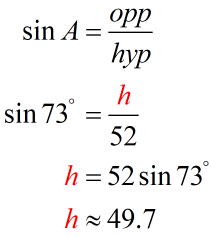
As you can see, side [latex]a[/latex] is less than the height, that is, [latex]41 < 49.7 \to a < h[/latex], which means that side [latex]a[/latex] is not long enough to form a triangle. Therefore, there exists no triangle! It follows that there is no solution to this triangle.

We can also check if our conclusion is correct. Let’s solve this problem as usual and see what we get. Our known ratio is [latex]\large{{\sin {{73}^\circ }} \over {41}}[/latex]. Side [latex]b[/latex] is given which means we can solve for angle [latex]\angle B[/latex] using the Law of Sines.

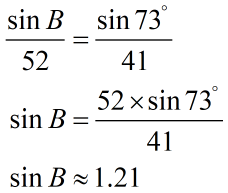
Because the value of sine can’t exceed [latex]1[/latex], it means there is no angle [latex]\angle B[/latex] such that [latex]\sin B \approx 1.21[/latex]. Therefore, our previous conclusion that no triangle exists is true!

---

Example 6: Solve triangle [latex]\triangle[/latex] [latex]ABC[/latex] if [latex]A=110^\circ[/latex], [latex]a=58[/latex], and [latex]b=67[/latex].

Let’s have a rough sketch of the triangle.

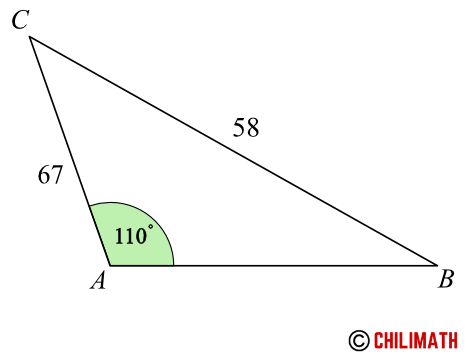
This is an SSA triangle and since angle [latex]A[/latex] is obtuse; and side [latex]a[/latex], [latex]58[/latex], is shorter than side [latex]b[/latex], [latex]67[/latex], that is, [latex]a<b[/latex], that means no triangle exists!

If we want to solve this using the Law of Sines, this is what we are going to get.

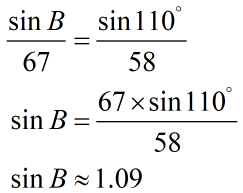
Given the fact that [latex]\left| {\sin B} \right| \le 1[/latex], it is obvious that we reached an invalid answer because we can’t allow the sine of an angle to be greater than [latex]1[/latex]. This means we can’t form a triangle with sides [latex]a=58[/latex], [latex]b=67[/latex], and angle [latex]\angle A =110^\circ[/latex].

---

Case 2: SSA Ambiguous Case – One Triangle

Given angle [latex]A[/latex] is acute, if side [latex]a[/latex] is greater than the height and side [latex]a[/latex] is greater than side [latex]b[/latex], then there is one triangle formed.

---

Given angle [latex]A[/latex] is obtuse, if side [latex]a[/latex] is greater than side [latex]b[/latex], then there is one triangle formed.

---

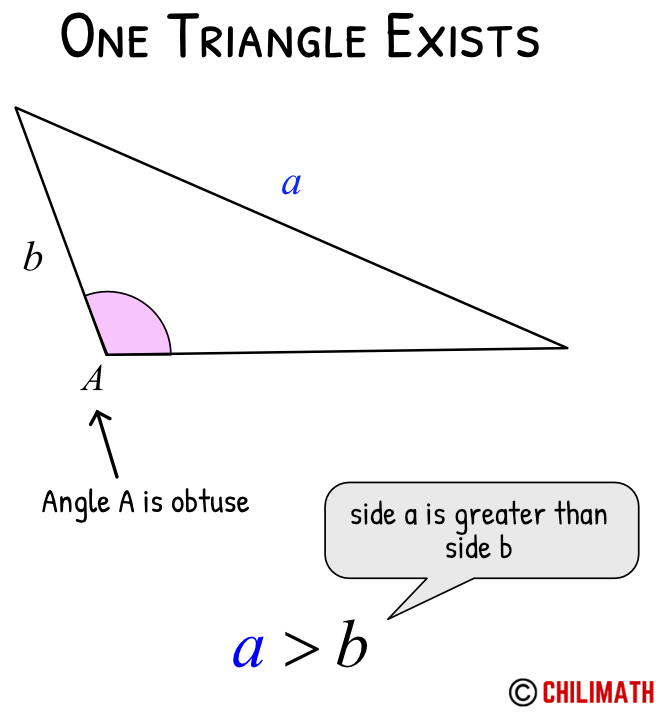
Example 7: Solve triangle [latex]\triangle[/latex] [latex]ABC[/latex] if [latex]A=70^\circ[/latex], [latex]a=47[/latex], and [latex]b=26[/latex].

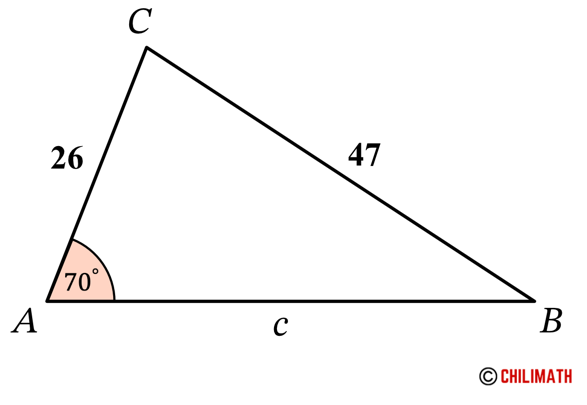
We are given two sides and a non-included angle which means we have an ambiguous case. The first thing that we can do is to compare the lengths of side [latex]a[/latex] and the height, [latex]h[/latex], given that angle [latex]A[/latex] is acute.

The height is calculated by the formula [latex]h = b\sin A[/latex] so we have

[latex]h = b\sin A[/latex] [latex]\\[/latex]

[latex]h = 26 \times \sin {70^\circ }[/latex] [latex]\\[/latex]

[latex]h \approx 24.4[/latex]

Since side [latex]a[/latex], [latex]47[/latex], is longer than the height, [latex]24.4[/latex], it means that at least one triangle is formed thus there is a solution to this triangle. So the next logical step is to figure out if there is one triangle or two triangles formed. This can easily be determined by comparing the lengths of side [latex]a[/latex] and side [latex]b[/latex]. 

If side [latex]a[/latex] is greater than side [latex]b[/latex], then we have one triangle. However, if side [latex]a[/latex] is less than side [latex]b[/latex] then we have two triangles.

Back to the problem, it is clear that side [latex]a[/latex] is greater than side [latex]b[/latex], that is, [latex]47 > 26[/latex]. Therefore, we have a case here where one triangle is formed. And so there’s no further steps needed to solve for the other triangle.

Now, let’s solve the triangle by calculating angle [latex]B[/latex], angle [latex]C[/latex], and side [latex]c[/latex].

To solve for angle [latex]B[/latex]:

To solve for angle [latex]C[/latex]:

Use the fact that sum of the measures of a triangle’s internal angles is equal to 180 degrees.

[latex]\angle A + \angle B + \angle C = {180^\circ }[/latex] [latex]\\[/latex]

[latex]\angle C = {180^\circ } – \angle A – \angle B[/latex] [latex]\\[/latex]

[latex]\angle C \approx {180^\circ } – {70^\circ } – {31^\circ }[/latex] [latex]\\[/latex]

[latex]\angle C \approx {79^\circ }[/latex]

To solve for side [latex]c[/latex]:

Now that we found angle [latex]C[/latex], we can now compute for side [latex]c[/latex] using the Law of Sines.

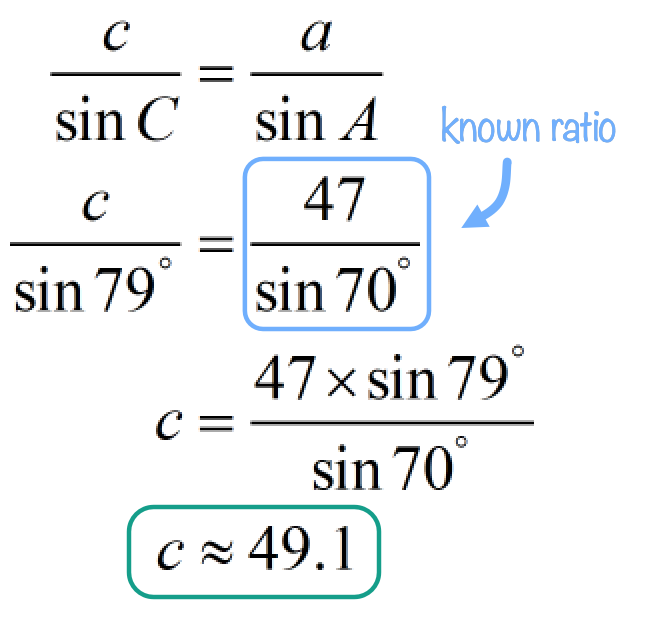
Therefore, the final solution is [latex]B \approx {31^\circ }[/latex], [latex]C \approx {79^\circ }[/latex], and [latex]c = 49.1[/latex].

---

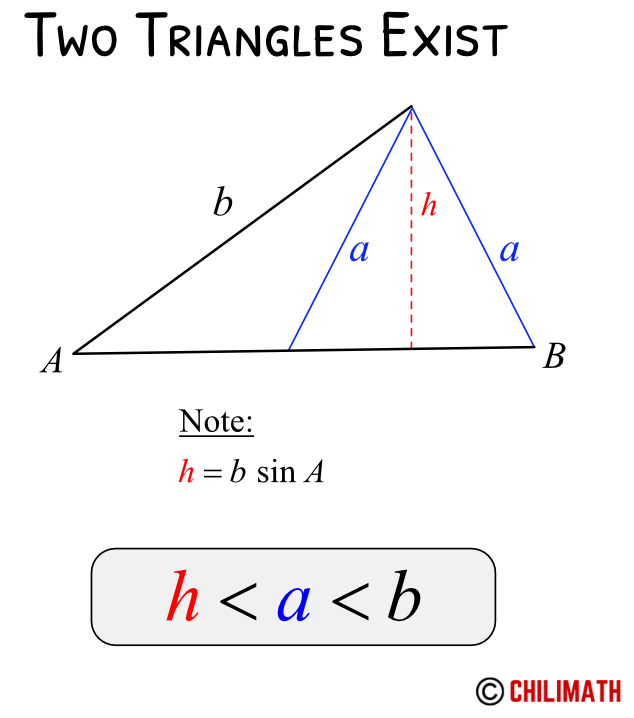
Case 3: SSA Ambiguous Case – Two Triangles

Given angle [latex]A[/latex] is acute, if side [latex]a[/latex] is greater than the height but less than side [latex]b[/latex], then there are two triangles formed.

---

Example 8: Solve triangle [latex]\triangle[/latex] [latex]ABC[/latex] if [latex]A=35^\circ[/latex], [latex]a=37[/latex], and [latex]b=55[/latex].

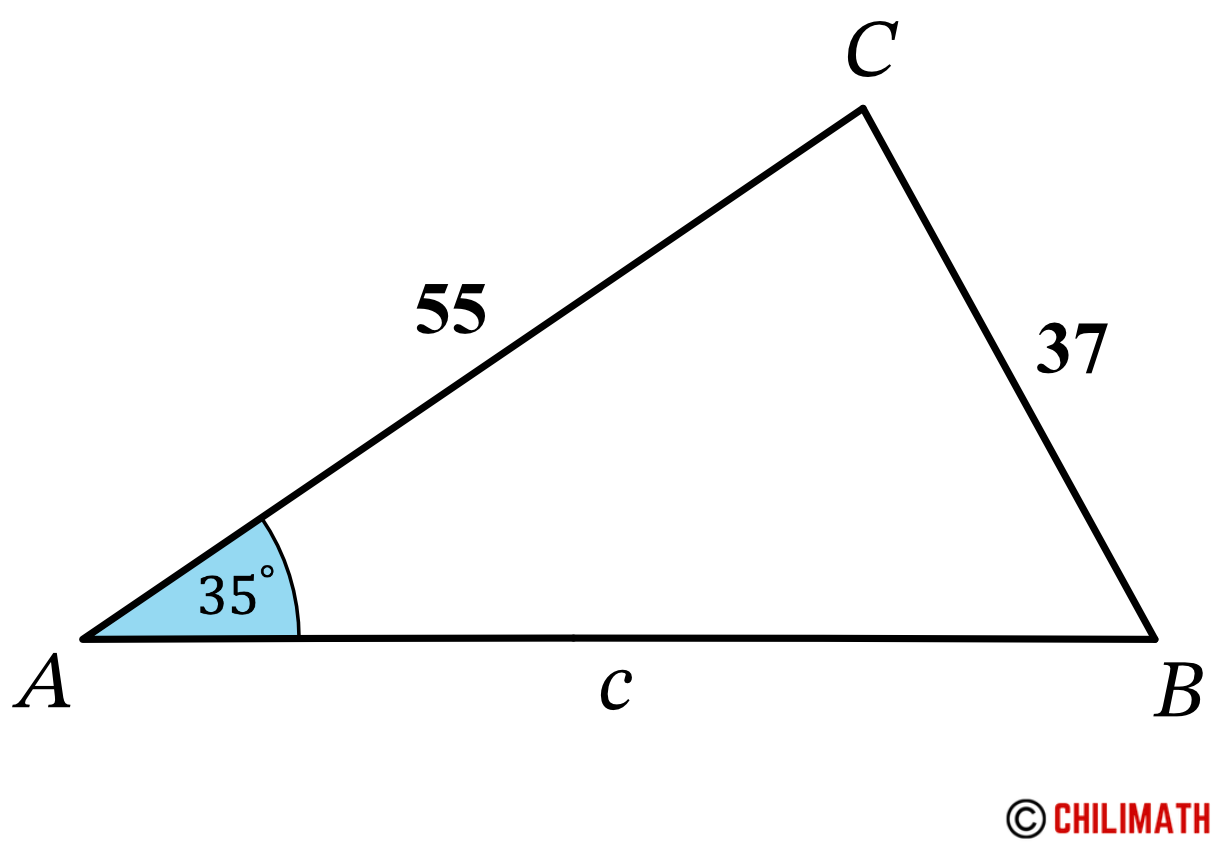
Given that angle [latex]A[/latex] is acute, the very first thing we need to verify is if side [latex]a[/latex] is longer than the height, [latex]h[/latex], otherwise no triangle exists. Let’s calculate the height.

[latex]h = b\sin A[/latex] [latex]\\[/latex]

[latex]h = 55 \times \sin {35^\circ }[/latex] [latex]\\[/latex]

[latex]h \approx 31.5[/latex]

Since side [latex]a>h[/latex], that is, [latex]37>31.5[/latex], then it guarantees us that at least one triangle is formed!

The next thing to check is to compare side sides [latex]a[/latex] and [latex]b[/latex].

If [latex]a>b[/latex], then there is one triangle. But, if [latex]a<b[/latex], then there are two triangles.

Since side [latex]a[/latex] is less than side [latex]b[/latex], that is, [latex]a < b \to 37 < 55[/latex], that means there are two triangles in this case.

Below are the two triangles (1) and (2) that are generated.

---

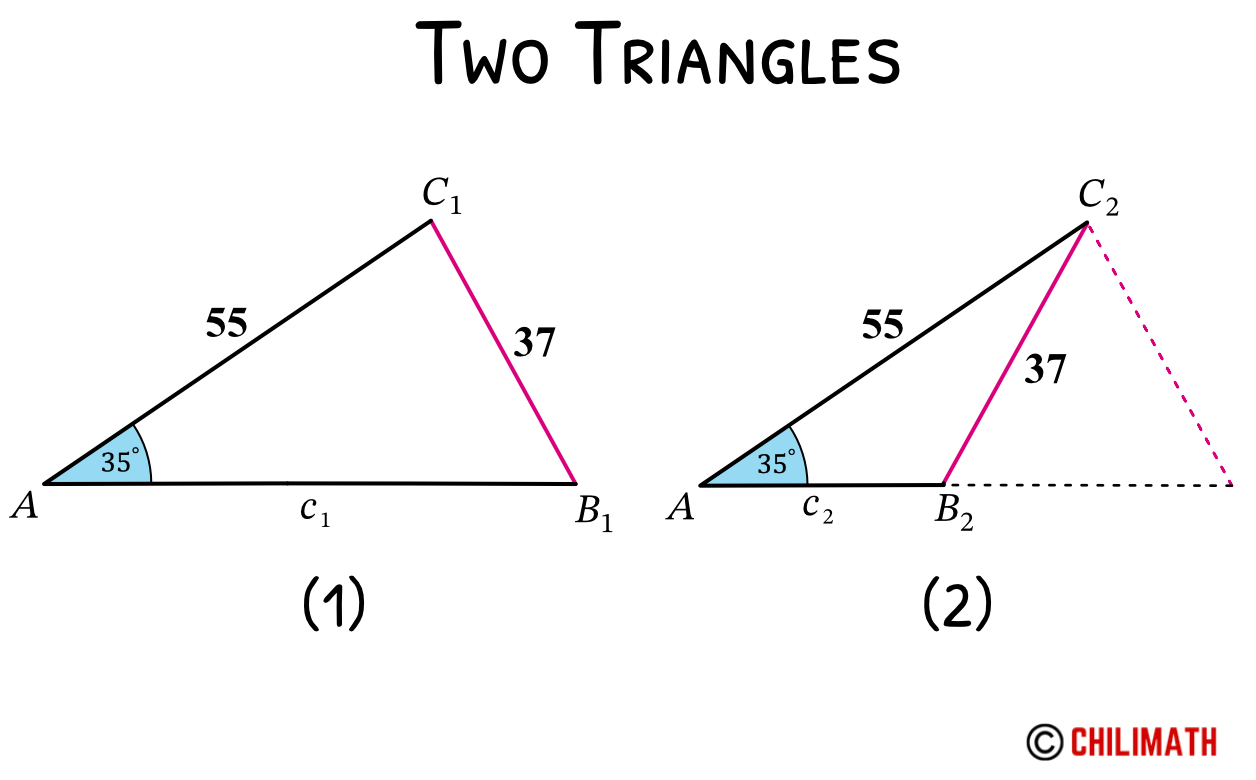
Solving Triangle 1

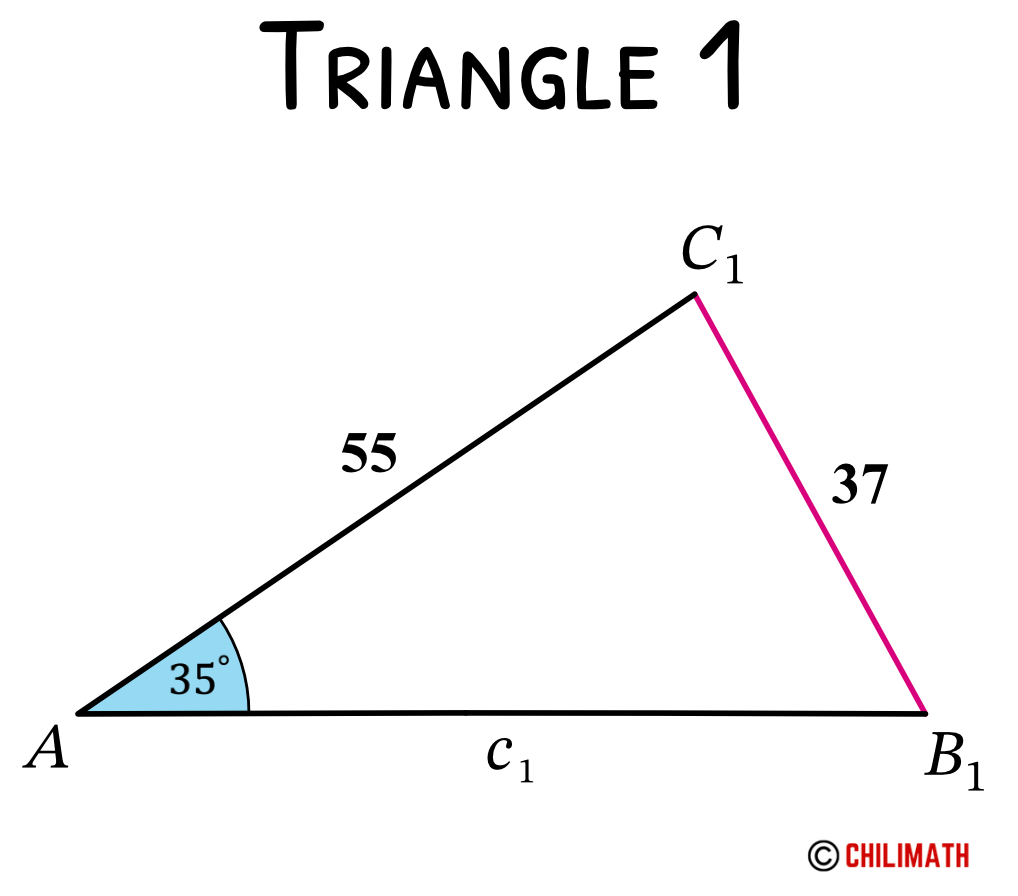
The known ratio here is angle [latex]A[/latex] and side [latex]a[/latex] which is [latex]\Large{{\sin A} \over a}[/latex] or [latex]\Large{a \over {\sin A}}[/latex]. Since side [latex]b[/latex] is given, we should be able to calculate angle [latex]{B_1}[/latex].

To solve for angle [latex]B_1[/latex]:

To solve for angle [latex]C_1[/latex]:

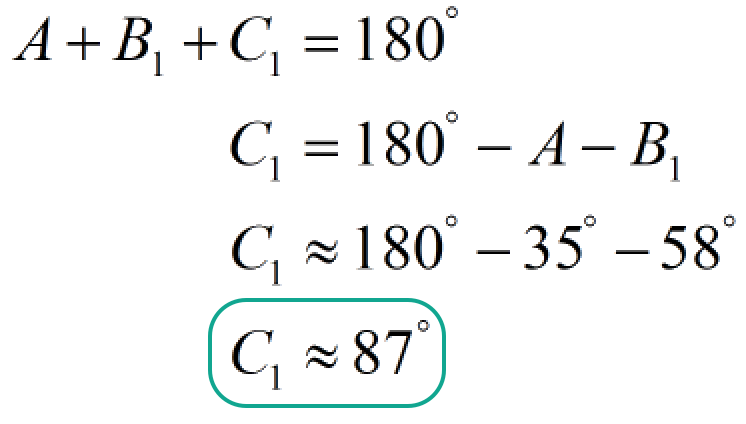
To solve for side [latex]c_1[/latex]:

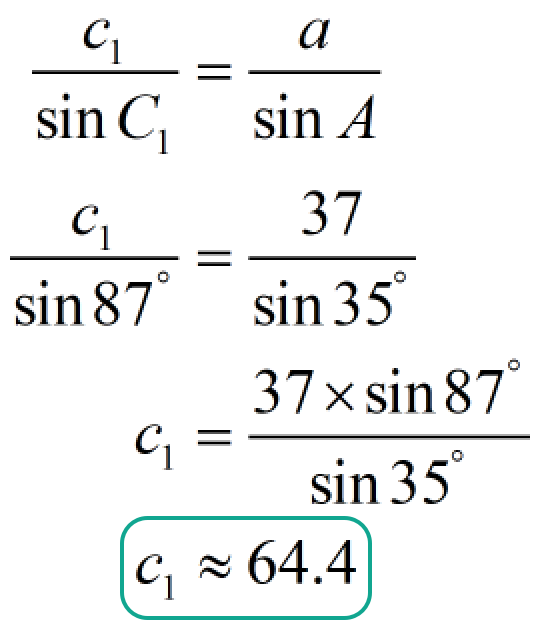
Therefore, the final solution for triangle 1 is [latex]{B_1} \approx {58^\circ }[/latex], [latex]{C_1} \approx {87^\circ }[/latex], and [latex]{c_1} \approx 64.4[/latex].

---

Now, we will solve triangle 2.

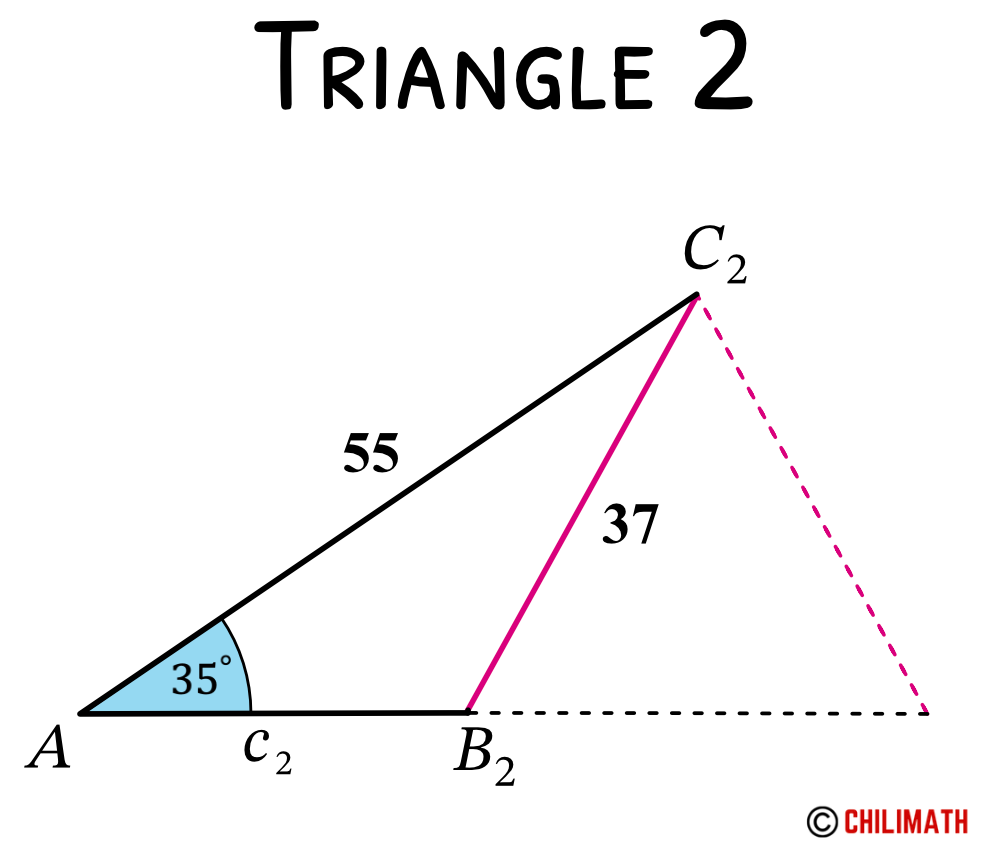
To solve for angle [latex]B_2[/latex]:

To find angle [latex]B_2[/latex], we simply need to get the supplement of angle [latex]B_1[/latex].

[latex]{B_2} = {180^\circ } – {B_1}[/latex] [latex]\\[/latex]

[latex]{B_2} \approx {180^\circ } – {58^\circ }[/latex] [latex]\\[/latex]

[latex]{B_2} \approx {122^\circ }[/latex]

To find angle [latex]{C_2}[/latex]:

We know that the sum of the internal angles of a triangle is 180 degrees.

[latex]A + {B_2} + {C_2} = {180^\circ }[/latex]

[latex]{C_2} = {180^\circ } – A – {B_2}[/latex]

[latex]{C_2} \approx {180^\circ } – {35^\circ } – {122^\circ }[/latex]

[latex]{C_2} \approx {23^\circ }[/latex]

To find side [latex]{c_2}[/latex]:

Therefore, the final solution for triangle 2 is [latex]{B_2} \approx {122^\circ }[/latex], [latex]{C_2} \approx {23^\circ }[/latex], and [latex]{c_2} \approx 25.2[/latex].