Order of Operations
The fundamental concept behind the order of operations is to perform arithmetic operators in the “right” order or sequence. Let’s take a look at how Rob and Patty tried to simplify a given numerical expression by applying the order or rule of operations.

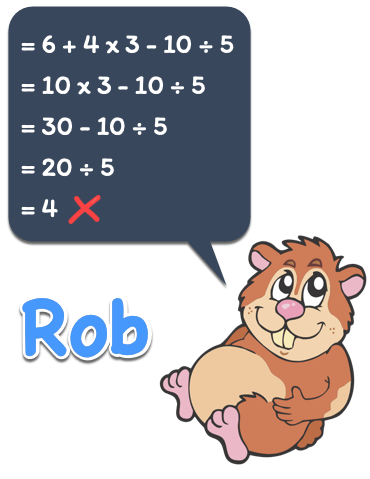
What is Rob’s mistake?
- He carelessly simplified the numerical expressions by applying arithmetic operations from left to right.
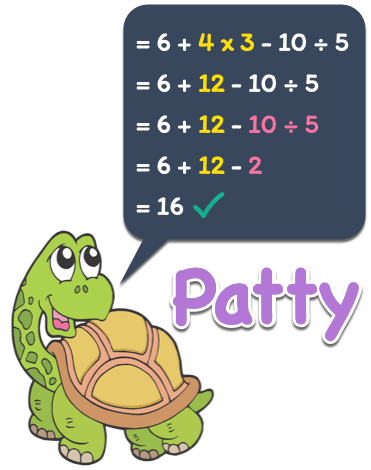
Patty got the correct answer because she properly applied the rules on order of operations.
- She performed multiplication and division first before addition and subtraction.
What is the Order of Operations?
The order of operations is merely a set of rules that prioritize the sequence of operations starting from the most important to the least important.
This rule on how to correctly simplify numerical expressions is also known as the PEMDAS Rule (an acronym for Please Excuse My Dear Aunt Sally).
Step 1: Do as much as you can to simplify everything inside the parenthesis or grouping symbol.
Step 2: Simplify exponential numbers in the numerical expression, wherever possible.
Step 3: Multiply and divide whichever comes first, from left to right
Step 4: Add and subtract whichever comes first, from left to right
Examples on How to Apply the Order of Operations to Simplify Numerical Expressions
Example 1: Simplify the expression below using the Order of Operations.
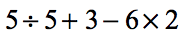
- Examining the numerical expressions with multiple operations from left to right, we can see that we must perform division first, which is [latex]5 \div 5 = 1[/latex].
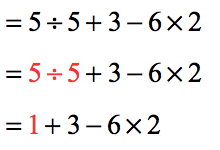
- At this point, I have three (3) possible operations. In the Order of Operations, multiplication takes precedence over addition and subtraction. Therefore, we should multiply next. We have [latex]6 \times 2 = 12[/latex].
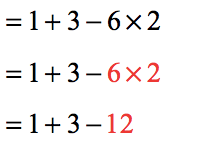
- What should we do next, add or subtract? Based on the Order of Operations, addition and subtraction are of equal importance. To determine which operation to perform first, we add or subtract whichever comes first from left to right which in this situation is to add, [latex]1 + 3 = 4[/latex].
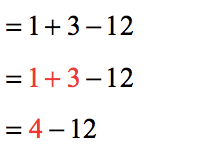
- Now we are left with one operation, subtraction. The seemingly complex numerical expression is reduced to the final answer of [latex] – 8[/latex].
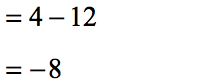
Example 2: Simplify the expression below using the Order of Operations.
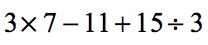
- Multiply
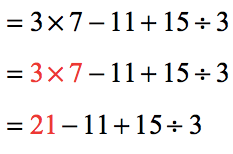
- Divide
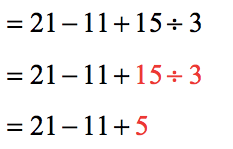
- Subtract
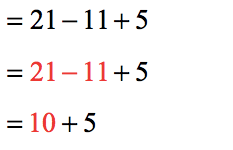
- Add
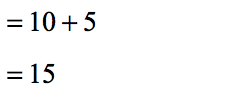
The next examples will involve parentheses. Remember that you have to simplify everything inside the parenthesis first before going forward.
Example 3: Simplify the expression below using the Order of Operations.
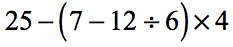
- Take a look at the expressions inside the parenthesis. The rule tells us to divide first before we subtract.
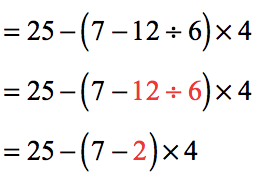
- We can get rid of the parenthesis by subtracting [latex]7[/latex] by [latex]2[/latex].

- Multiplication is much “stronger” operation that subtraction that’s why we must first multiply [latex]5[/latex] and [latex]4[/latex].
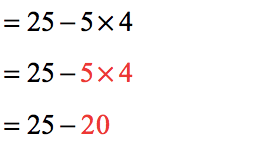
- Finish it off by subtracting [latex]25[/latex] by [latex]20[/latex].
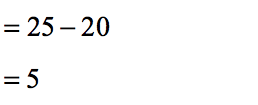
Example 4: Simplify the expression below using the Order of Operations.
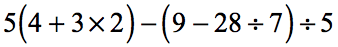
- Simplify the expressions inside the parentheses first. Multiply on the first parenthesis and divide on the second.
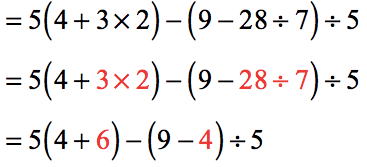
- Add the numbers inside the first parenthesis then subtract the numbers inside the second.
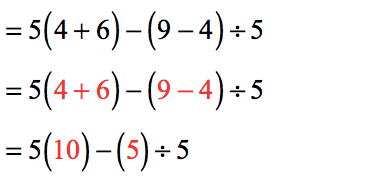
- We have multiplication and division here. Since multiplications comes before division, we are going to multiply first.
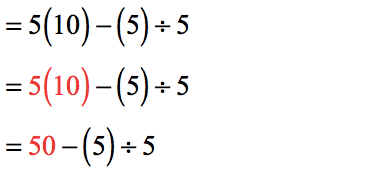
- Between subtracting and dividing, division takes precedence therefore we divide [latex]5[/latex] by [latex]5[/latex] to get [latex]1[/latex].
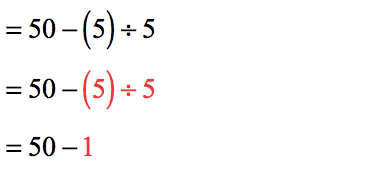
- The last operation left is subtraction therefore that’s what we’re going to do.

The final examples will involve exponents so be careful with each step because they are so many things going on. As long as you remain focus in following the rules governing the order of operations, it shouldn’t be that difficult! Here we go…
Example 5: Simplify numerical expression below using the rules of Order of Operations.
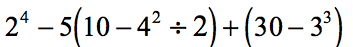
- Simplify the expressions inside the parentheses. But more specifically, simplify the numbers with exponents.
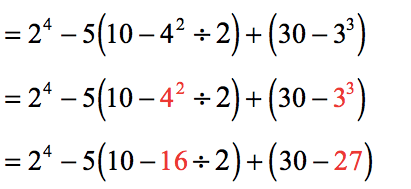
- There are two parentheses to simplify. We will simplify the second one which is [latex]\left( {30 – 27} \right)[/latex] because it is much simpler. Here, the difference of [latex]30[/latex] and [latex]27[/latex] is [latex]3[/latex].
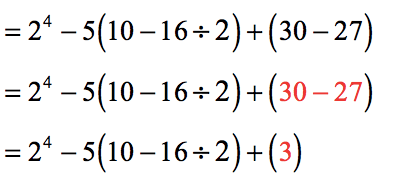
- Now we turn our attention to the other parenthesis. The Order of Operations tells us to divide before we subtract.
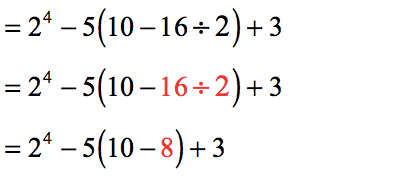
- Finally we can get rid of the parenthesis by performing subtraction as there is no other thing to do.
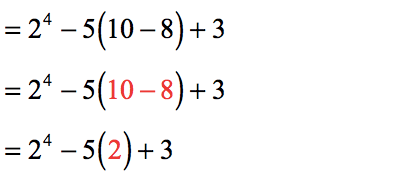
- Looking at what we have left, simplifying exponential numbers takes precedence over the operations of multiplication, addition, and subtraction.
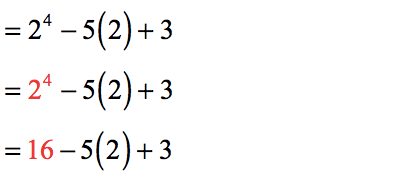
- Scanning from left to right, it’s obvious that we must multiply before adding and/or subtracting.
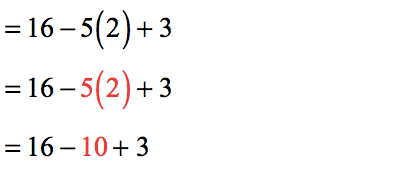
- Based on the Order of Operations, addition and subtraction are of equal importance. We must subtract first because the operation of subtraction comes before addition when viewed from left to right.
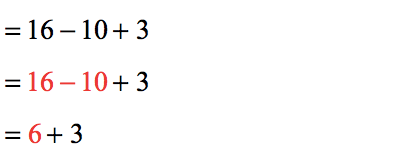
- The last step is to add because there is no other operations left.

Example 6: Simplify the expression below using the Order of Operations.
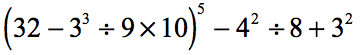
- Focus our attention on the single grouping symbol which is the parenthesis. Notice that there is a number with an exponent. Let’s simplify [latex]{3^3}[/latex] first.
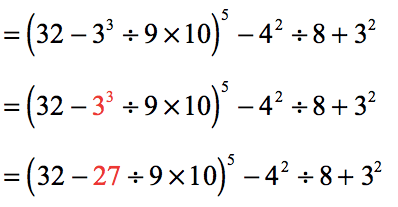
- Looking inside the parenthesis, we must divide first before multiplying and subtracting.
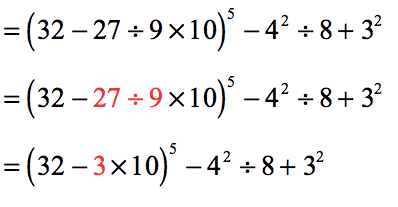
- Keeping still our attention inside the parenthesis, the order of operations tells us to multiply before we subtract.
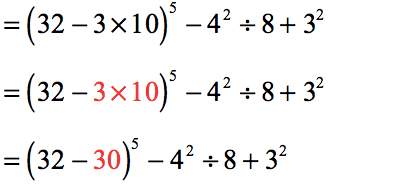
- The last operation left inside the parenthesis is subtraction. Let’s perform that!
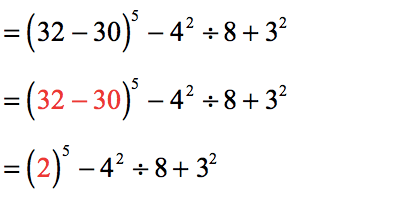
- Let’s take a pause here. At this point, it is clear that we can perform three (3) simplifications simultaneously. It’s obvious to see that we have three exponential expressions which are [latex]{2^5}[/latex], [latex]{4^2}[/latex], and [latex]{3^2}[/latex].
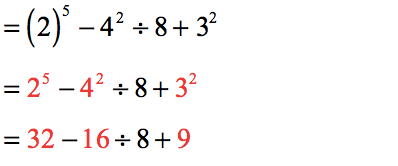
- The seemingly complex problem is now reduced to something that is very easy to simplify. Looking at it from left to right, division takes precedence over subtraction and addition.
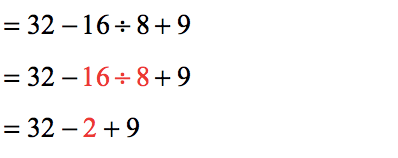
- Because subtraction and multiplication are on the same level in the hierarchy of operations. The way we break the tie as you should already know it is to perform the one that comes first when viewed from left to right. In this situation, we will subtract then add. That’s it!
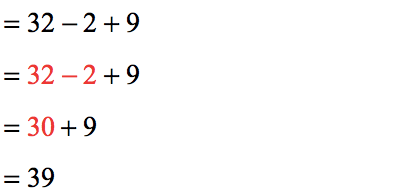
Take a Quiz
You may also be interested in these related math lessons or tutorials:
