How to Multiply and Divide Positive and Negative Numbers
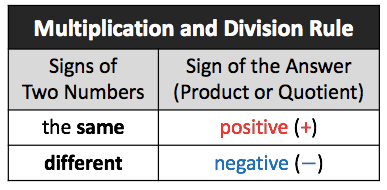
The rules that govern multiplication and division of numbers are very similar. The key is to identify if the signs of the given two numbers are the same, or different because this will determine the final sign of the answer.
Multiplication and Division Rules of Signed Numbers
Examples of How to Find the Product or Quotient of Signed Numbers
Example 1: Find the product of (3)(6) and the quotient of 12 ÷ 6.
- Find the product of (3)(6):
Since the numbers 3 and 6 have the same signs (both positive), their product is positive.
(3)(6) = 18
- Find the quotient of 12 ÷ 6:
Since the numbers 12 and 6 have the same signs (both positive), their quotient is positive.
12 ÷ 6 = 2
Example 2: Find the product of (–5)(–3) and the quotient of –21 ÷ (–7).
- Find the product of (–5)(–3):
The numbers −5 and −3 both have negative signs. Having the same sign means that their product must also be positive.
(–5)(–3) = 15
- Find the quotient of –21 ÷ (–7):
The numbers −5 and −3 both have negative signs. The quotient of two numbers with the same sign is positive.
–21 ÷ (–7) = 3
Example 3: Multiply the numbers (9)(–3) and divide the numbers 18 ÷ (–9).
- Multiplying (9)(–3):
The number 9 has a positive sign while the number −3 has a negative sign. Multiplying these two numbers with different signs should output a negative answer.
(9)(–3) = –27
- Dividing 18 ÷ (–9):
The number 9 is positive while −3 is negative. Dividing two numbers with different signs should give a negative answer.
18 ÷ (–9) = –2
Example 4: Simplify the numerical expression.
![[(-6)(4)]/[(-12)(-1)](https://www.chilimath.com/wp-content/uploads/2019/01/mdnum-ex4a.png)
What we can do is to simplify the numerator by multiplying the two numbers. Do the same thing with the denominator.
The numbers on the numerator have different signs, therefore we expect their product to be negative. Meanwhile, the denominator has two numbers with the same sign (both negative), and so their product must be positive.
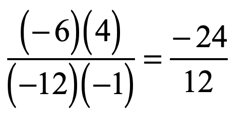
We finish this off by dividing the numerator by the denominator. Don’t forget the division rule as well. The numerator is negative while the denominator is positive, by having different signs should yield a negative answer.
![[(-6)(4)]/[(-12)(-1)=-2](https://www.chilimath.com/wp-content/uploads/2019/01/mdnum-ex4c.png)
Example 5: Multiply the numbers (–1)(–2)(–3)(–4).
So far, we have been multiplying numbers two at a time. This time around, we have a situation of finding the product of three or more numbers.
We can work this out by multiplying two numbers at a time because we know how to do it that way.
But there is a quick method to figure out the sign without having to multiply them two at a time.
Observe that we have an even number of negative signs, that is, four negative numbers. If you encounter something like this, use the rule:

An even number of negative signs means that we expect the answer to be positive.
(–1)(–2)(–3)(–4) = +24
Example 6: Multiply the numbers (–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1).
This problem is not intended to trick you. Instead, think of it as another opportunity to learn how to handle questions just like this. Your teacher may throw something similar to this in your quiz to test if you know the topic fully well.
Without paying attention to the signs, all numbers are just ones. Therefore, we predict that the answer may either be +1 or −1.
Counting the number of negative signs, we have a total of nine (9) which is odd!
Remember the rule,

An odd number of negative signs implies that our final answer must be negative.
(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)(–1)= –1
Example 7: Divide the numbers (–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1).
The rule for odd and even number of negative numbers also work when dividing numbers.
Since we have a count of seven (7) negative signs, an odd number, the answer must be negative.
(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1) ÷(–1)= –1
