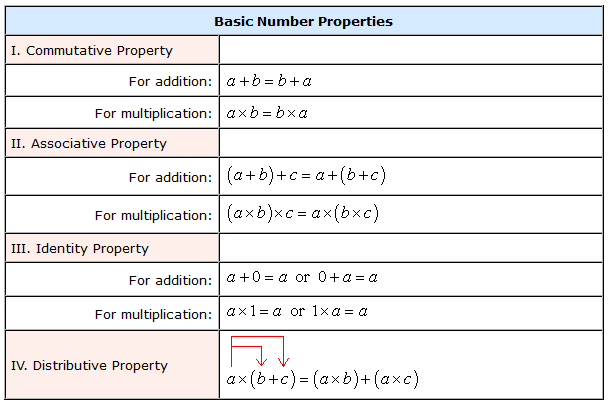
Basic Number Properties
The basic properties of real numbers are based on a straightforward concept. You could even call it “common sense” math because no complicated analysis is required. Real numbers have four (4) fundamental properties: commutative, associative, identity, and distributive. These properties are only applicable to addition and multiplication operations.
I. Commutative Property
For Addition
The sum of two or more real numbers is always the same regardless of the order in which they are added. In other words, real numbers can be added in any order because the sum remains the same.
Examples:
a) [latex]a + b = b + a[/latex]
b) [latex]5 + 7 = 7 + 5[/latex]
c) [latex]{}^ – 4 + 3 = 3 + {}^ – 4[/latex]
d) [latex]1 + 2 + 3 = 3 + 2 + 1[/latex]
For Multiplication
The product of two or more real numbers is not affected by the order in which they are being multiplied. In other words, real numbers can be multiplied in any order because the product remains the same.
Examples:
a) [latex]a \times b = b \times a[/latex]
b) [latex]9 \times 2 = 2 \times 9[/latex]
c) [latex]\left( { – 1} \right)\left( 5 \right) = \left( 5 \right)\left( { – 1} \right)[/latex]
d) [latex]m \times {}^ – 7 = {}^ – 7 \times m[/latex]
II. Associative Property
For Addition
The sum of two or more real numbers is always the same regardless of how you group them. When you add real numbers, any change in their grouping does not affect the sum.
Examples:
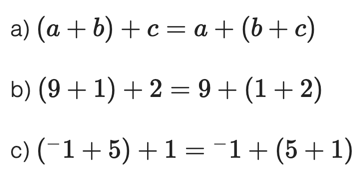
For Multiplication
The product of two or more real numbers is always the same regardless of how you group them. When you multiply real numbers, any change in their grouping does not affect the product.
Examples:
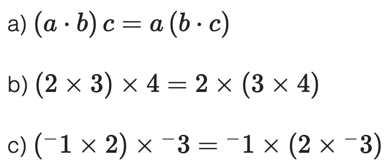
III. Identity Property
For Addition
Any real number added to zero (0) is equal to the number itself. Zero is the additive identity since [latex]a + 0 = a[/latex] or [latex]0 + a = a[/latex]. You must show that it works both ways!
Examples:
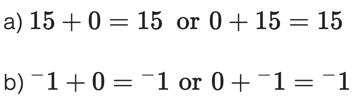
For Multiplication
Any real number multiplied by one (1) is equal to the number itself. The number one is the multiplicative identity since [latex]a \times 1 = a[/latex] or [latex]1 \times a = 1[/latex]. You must show that it works both ways!
Examples:
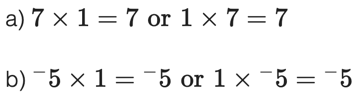
IV. Distributive Property of Multiplication over Addition
Multiplication distributes over Addition
Adding two or more real numbers and multiplying the sum to an outside number, is the same as multiplying the outside number to every number inside the parenthesis, then adding their products.
Examples:
a)
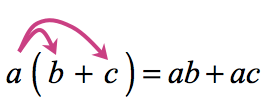
b)
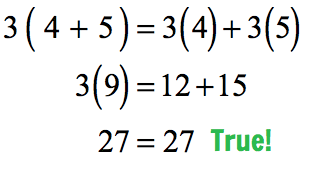
c)
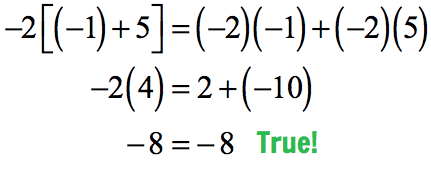
The following is the summary of the properties of real numbers as discussed above: