Graphs of Parent Functions
A parent function is the simplest form that a function can be. Its basic shape is not in any way altered.
For instance, when you see a u-shaped graph that is inverted and vertically stretched, you should still recognize that it is a parabola which has undergone different transformations.
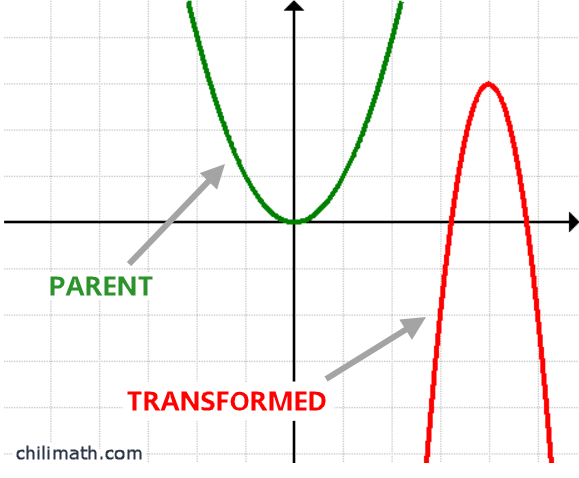
That is, if [latex]y = a{x^2} + bx + c[/latex] is the general form of a quadratic function, then its parent function is simply [latex]y=x^2[/latex] since it’s the simplest of its kind in the family.
List of Parent Functions
The graphs of the most frequently used parent functions are shown below. It’s a useful mathematical skill to be able to recognize them just by looking at their fundamental shapes.
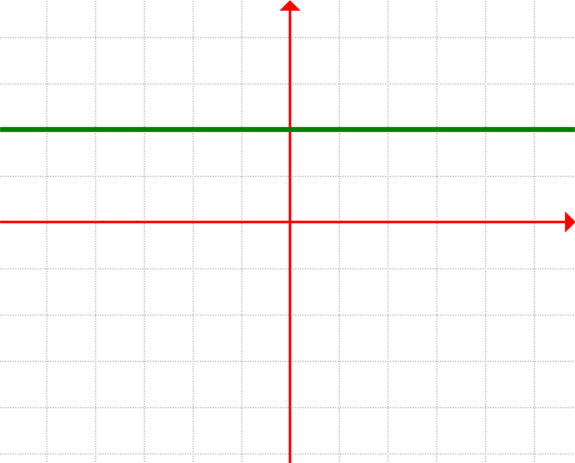
- Constant Function
[latex]\large{f\left( x \right) = c}[/latex]
where [latex]\large{c}[/latex] is a number
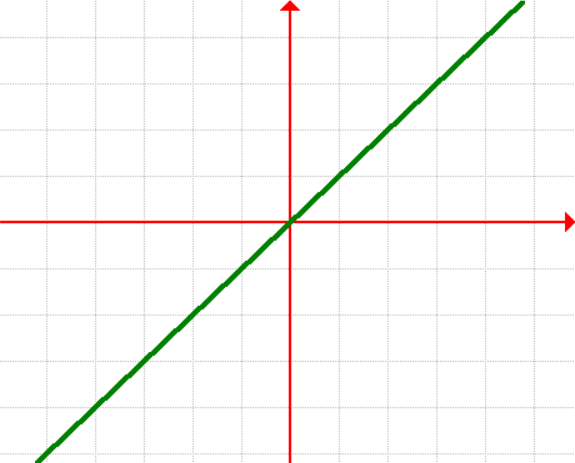
2. Linear Function
[latex]\large{f\left( x \right) = x}[/latex]
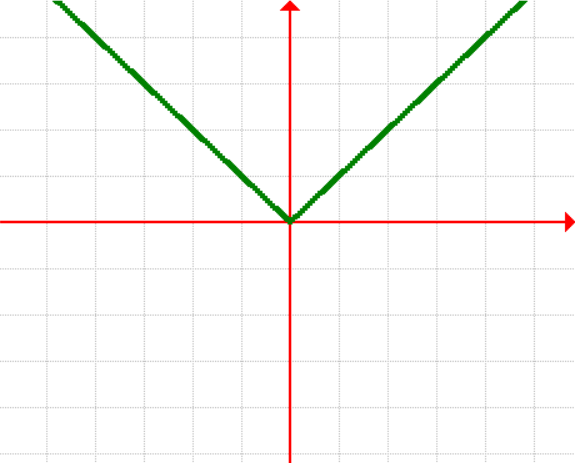
3. Absolute Value Function
[latex]\large{f\left( x \right) = \left| x \right|}[/latex]
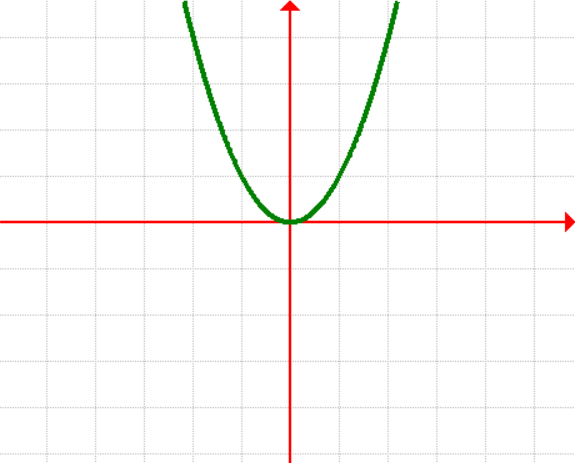
4. Quadratic Function
[latex]\large{f\left( x \right) = {x^2}}[/latex]
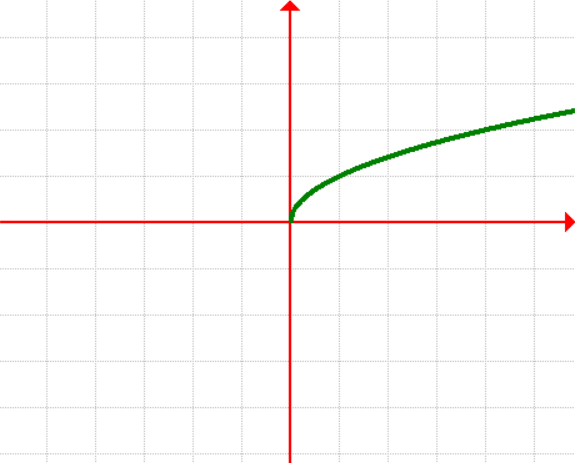
5. Square Root Function
[latex]\large{f\left( x \right) = \sqrt x }[/latex]
6. Cubic Function
[latex]\large{f\left( x \right) = {x^3}}[/latex]

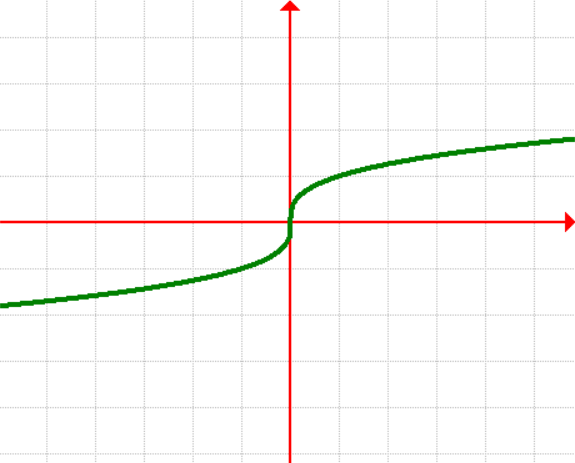
7. Cube Root Function
[latex]\large{f\left( x \right) = \sqrt [3] {x}}[/latex]
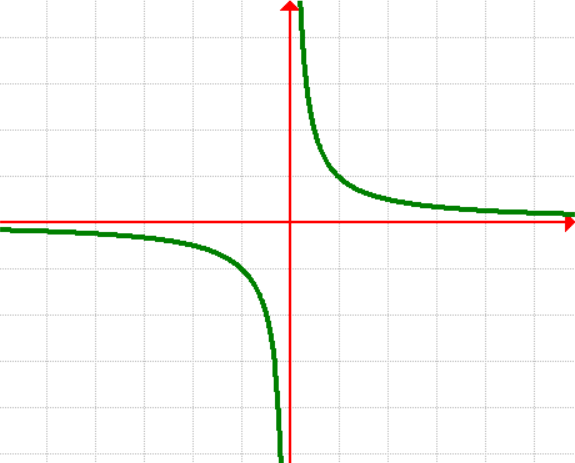
8. Rational Function
[latex]\large{f\left( x \right) = \Large{{1 \over x}}}[/latex]
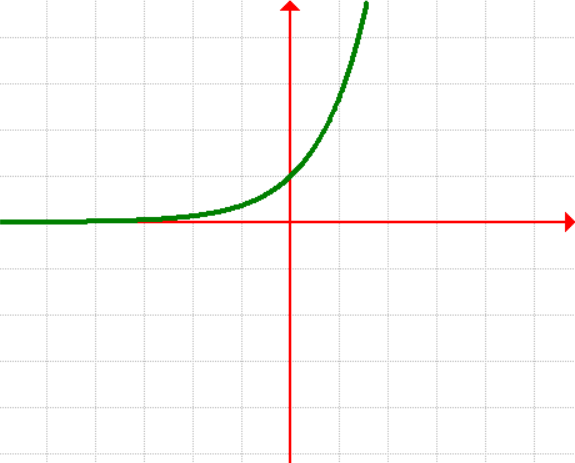
9. Exponential Function
[latex]\large{f\left( x \right) = {e^x}}[/latex]
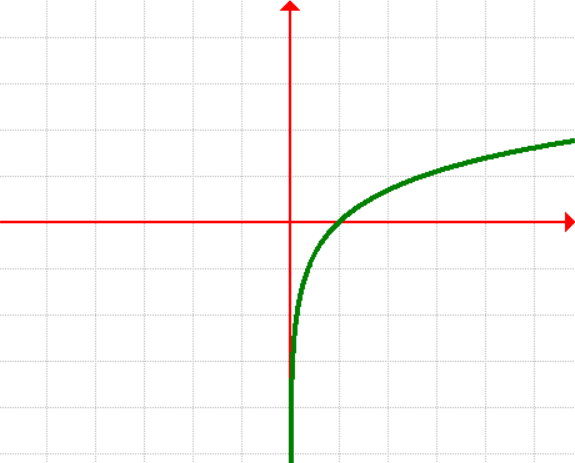
10. Logarithmic Function
[latex]\large{f\left( x \right) = \ln \left( x \right)}[/latex]