Absolute Value Equations Practice Problems with Answers
There are eleven (11) practice problems in this collection regarding absolute value equations. Whether you’re a beginner or seeking a challenge, there’s something here for you. As you tackle each problem, remember that in every attempt, right or wrong, fuels your mathematical growth. Good luck!
Problem 1: Solve the absolute value equation below.
[latex]\left| {x + 2} \right| = – 3[/latex]
Answer
Since the absolute value can’t be negative, therefore it has [latex]\color{red}\text{no solution}[/latex].
Problem 2: Solve the absolute value equation below.
[latex]\left| {2x \,- \,3} \right| = 7[/latex]
Answer
Solve the positive and negative cases.

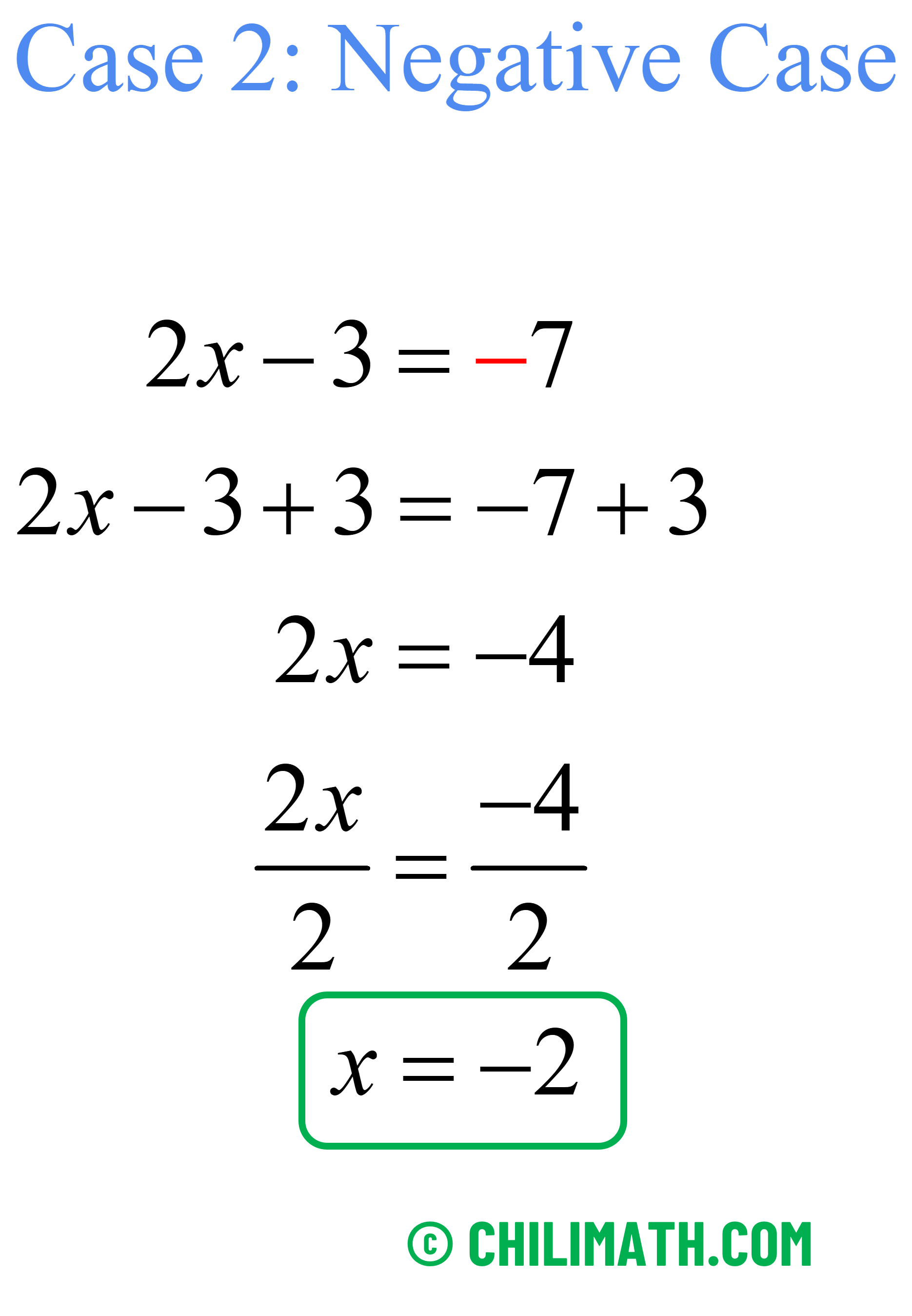
Therefore, the solution set is [latex]\{ – 2,5\}[/latex].
Problem 3: Solve the absolute value equation below.
[latex] – 7\left| {x\, – \,2} \right| = – 21[/latex]
Answer
Isolate the absolute value expression on the left side by dividing both sides of the equation by [latex]-7[/latex]
\begin{align*} – 7\left| {x – 2} \right| = – 21 \\ \\ {{ – 7\left| {x – 2} \right|} \over { – 7}} = {{ – 21} \over { – 7}} \\ \\ \left| {x – 2} \right| = 3 \end{align*}Now, break the absolute value equation into two cases then solve.

Therefore, the solution set is [latex]{ – 1,5}[/latex].
Problem 4: Solve the absolute value equation below.
[latex]4\, – \,\left| {3x\,+ \,6} \right| = 1[/latex]
Answer
Isolate the absolute value expression by subtracting [latex]4[/latex] from both sides. Then, divide [latex]-1[/latex] from both sides.
\begin{align*} 4 – \left| {3x + 6} \right| &= 1 \\ \\ 4 – 4 – \left| {3x + 6} \right| &= 1 – 4 \\ \\ – \left| {3x + 6} \right| &= – 3 \\ \\ {{ – \left| {3x + 6} \right|} \over { – 1}} &= {{ – 3} \over { – 3}} \\ \\ \left| {3x + 6} \right| &= 3 \end{align*}Break the absolute value equation into two equations with positive and negative cases then solve.

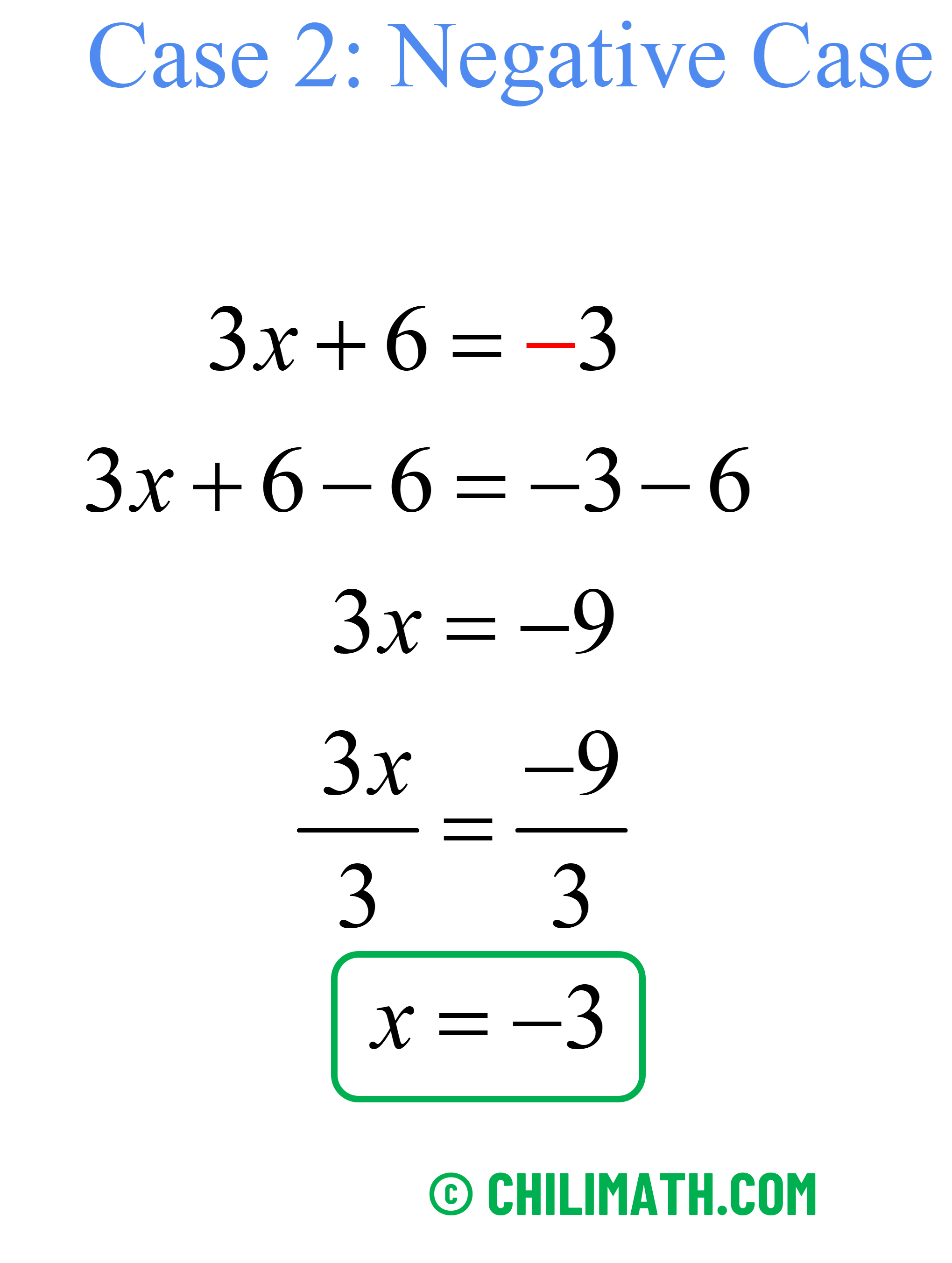
Therefore, the solution set is [latex]\{ – 3,-1\}[/latex].
Problem 5: Solve the absolute value equation below.
[latex]\left| {x \,- \,{1 \over 2}} \right| + \left| {x \, – \,{1 \over 2}} \right| = 7[/latex]
Answer
The absolute value expressions on the left side are similar terms therefore we can combine them.
\begin{align*} \left| {x \,-\, {1 \over 2}} \right| + \left| {x \,- \,{1 \over 2}} \right| &= 7 \\ \\ 2\left| {x\, – \,{1 \over 2}} \right| &= 7 \end{align*}Finally, divide [latex]2[/latex] from sides of the equation to isolate the absolute value expression.
\begin{align*} & {{2\left| {x\, -\, {1 \over 2}} \right|} \over 2} = {7 \over 2} \\ \\ & \left| {x \,- \,{1 \over 2}} \right| = {7 \over 2} \end{align*}Now, we solve each case.

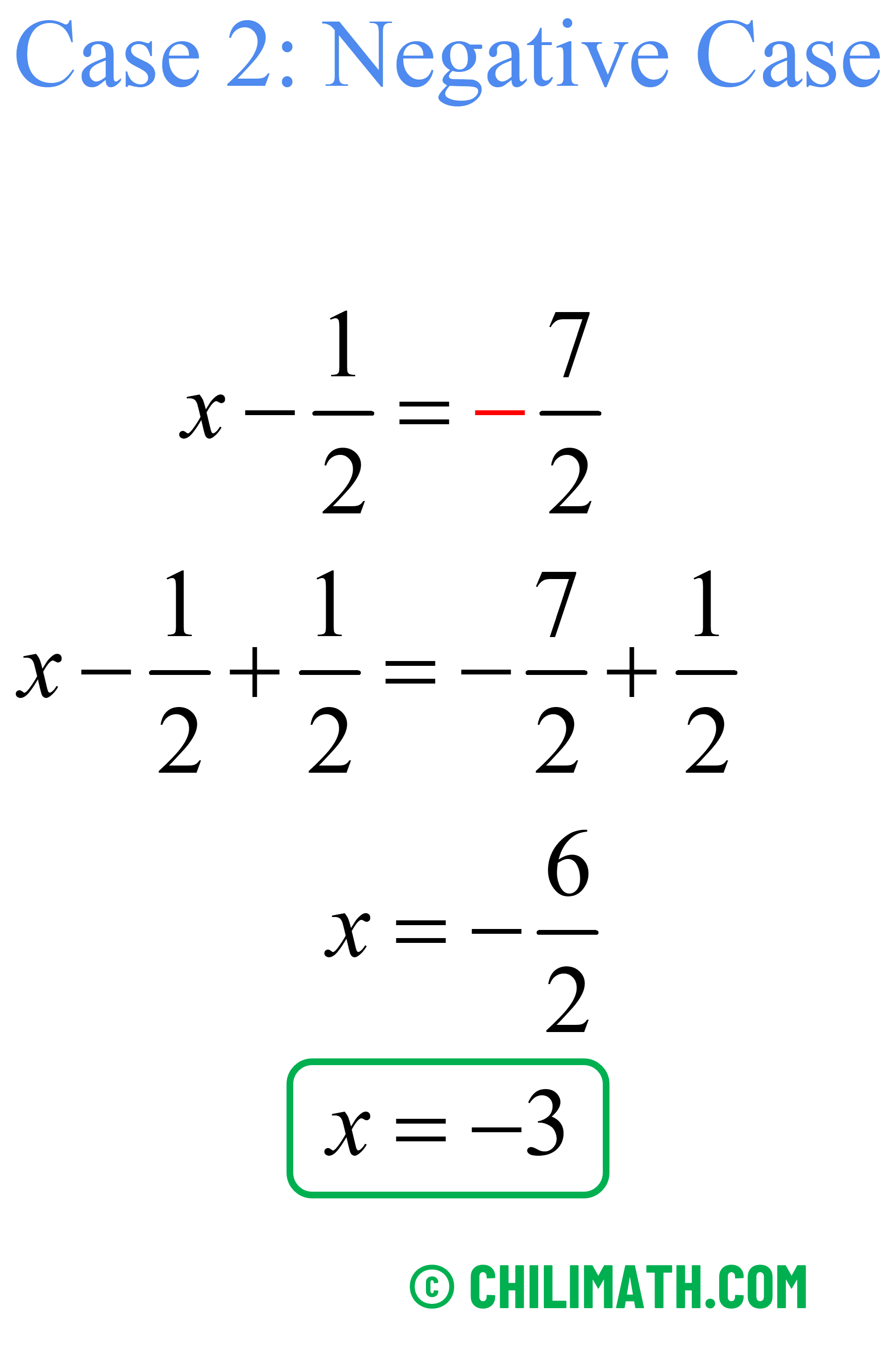
Therefore, the solution set is [latex]\{ – 3,4\}[/latex].
Problem 6: Solve the absolute value equation below.
[latex]\left| {3{x^2}\, – \,2x} \right| = 5[/latex]
Answer
Split the absolute value equation into two cases then solve.
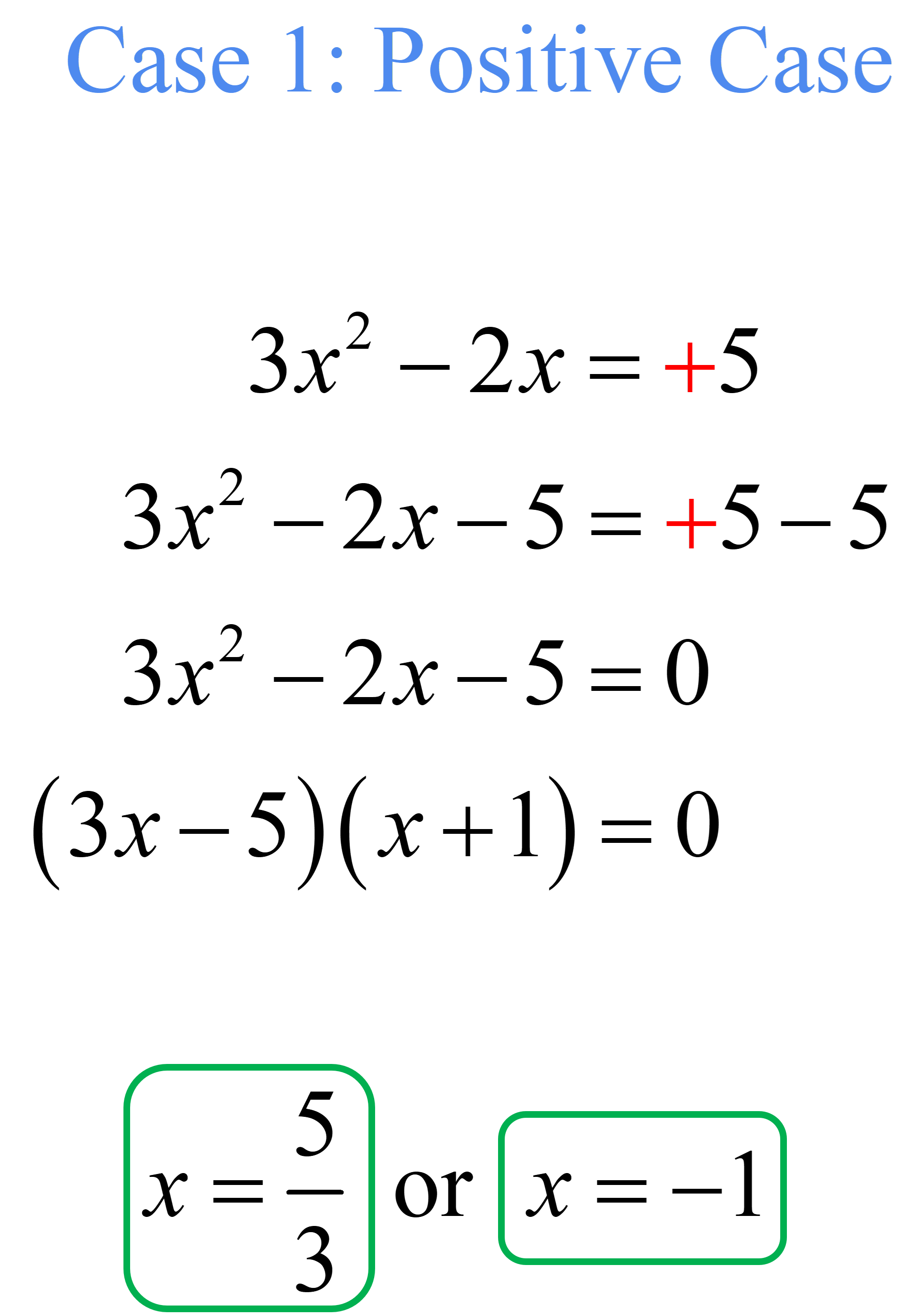

Therefore, the solution set is [latex]\{ – 1,{\large{5 \over 3}}\}[/latex].
Problem 7: Solve the absolute value equation below.
[latex]{\Large\left| {{{x \,- \,2} \over {x\, + \,1}}} \right|} ={ \Large{1 \over 2}}[/latex]
Answer
Separate the absolute value equation into positive and negative cases then solve.

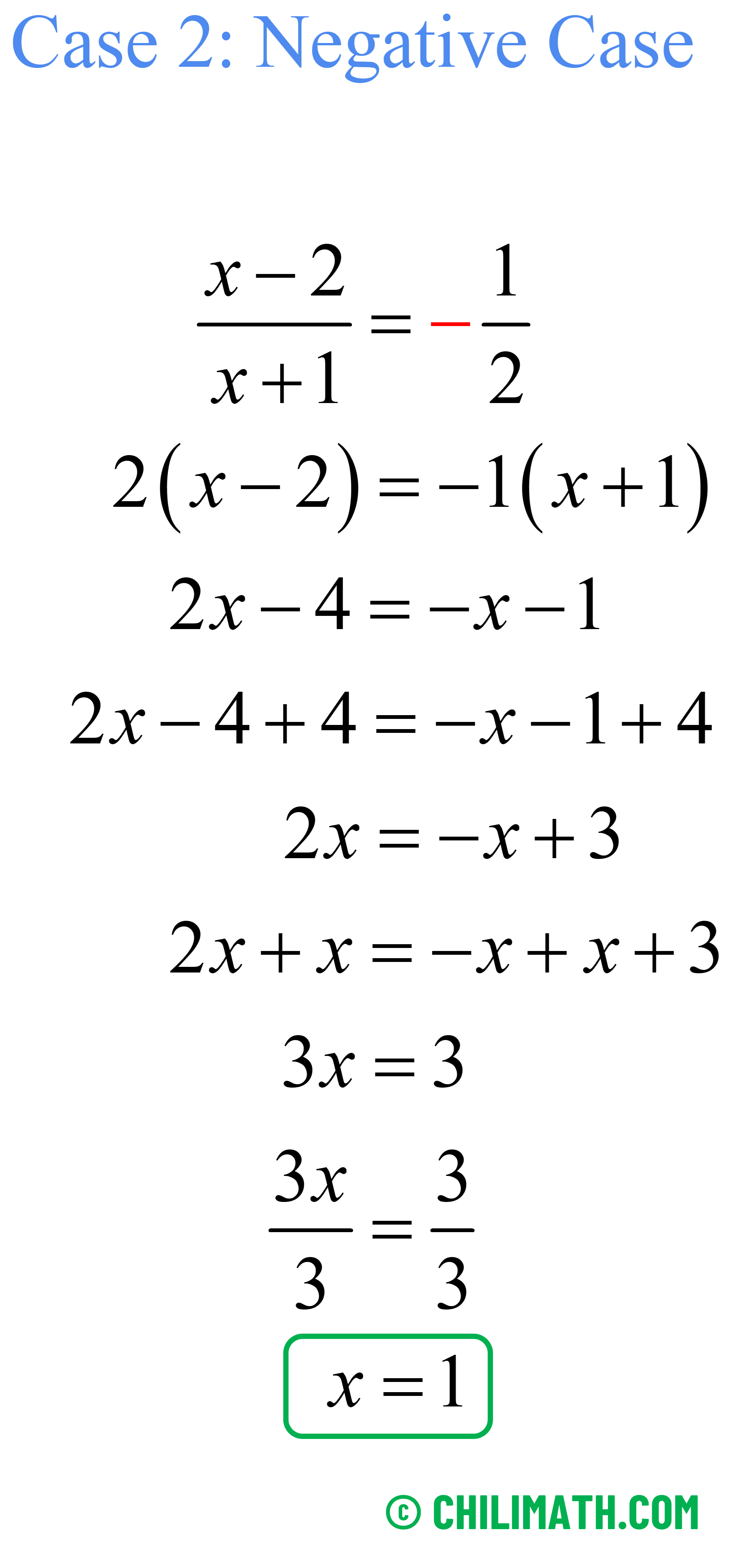
Therefore, the solution set is [latex]\{ 1,5\}[/latex].
Problem 8: Solve the absolute value equation below.
[latex]\left| {x\, – \,8} \right| = 2x\, -\, 1[/latex]
Answer
Consider the positive and negative cases then solve each equation.

Validate the answer [latex]x=-7[/latex] if it is indeed a solution by plugging it back into the original absolute value equation.
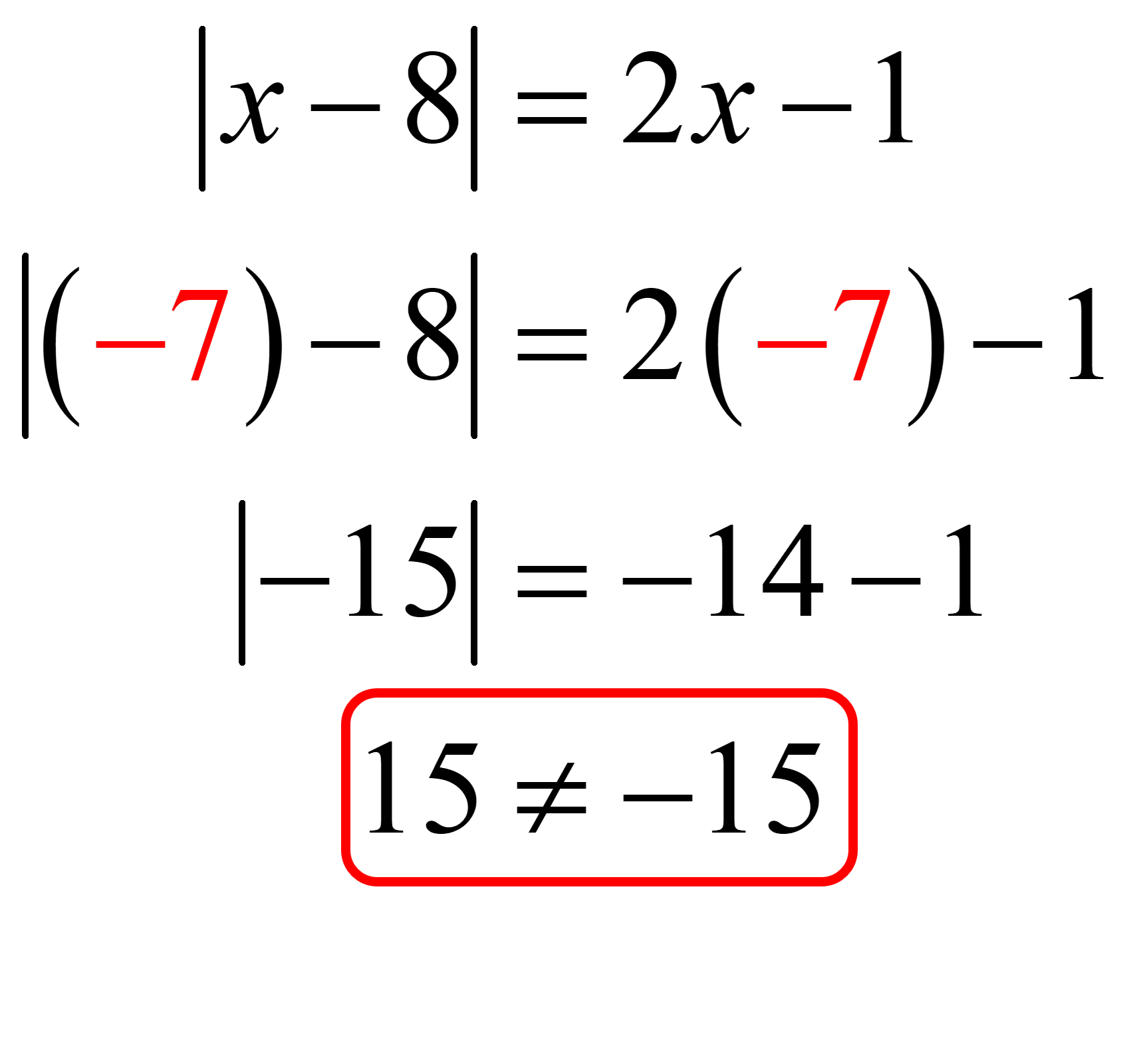
We arrived at a contradiction since [latex]15=-15[/latex] is false. That means [latex]x=-7[/latex] is not a solution.
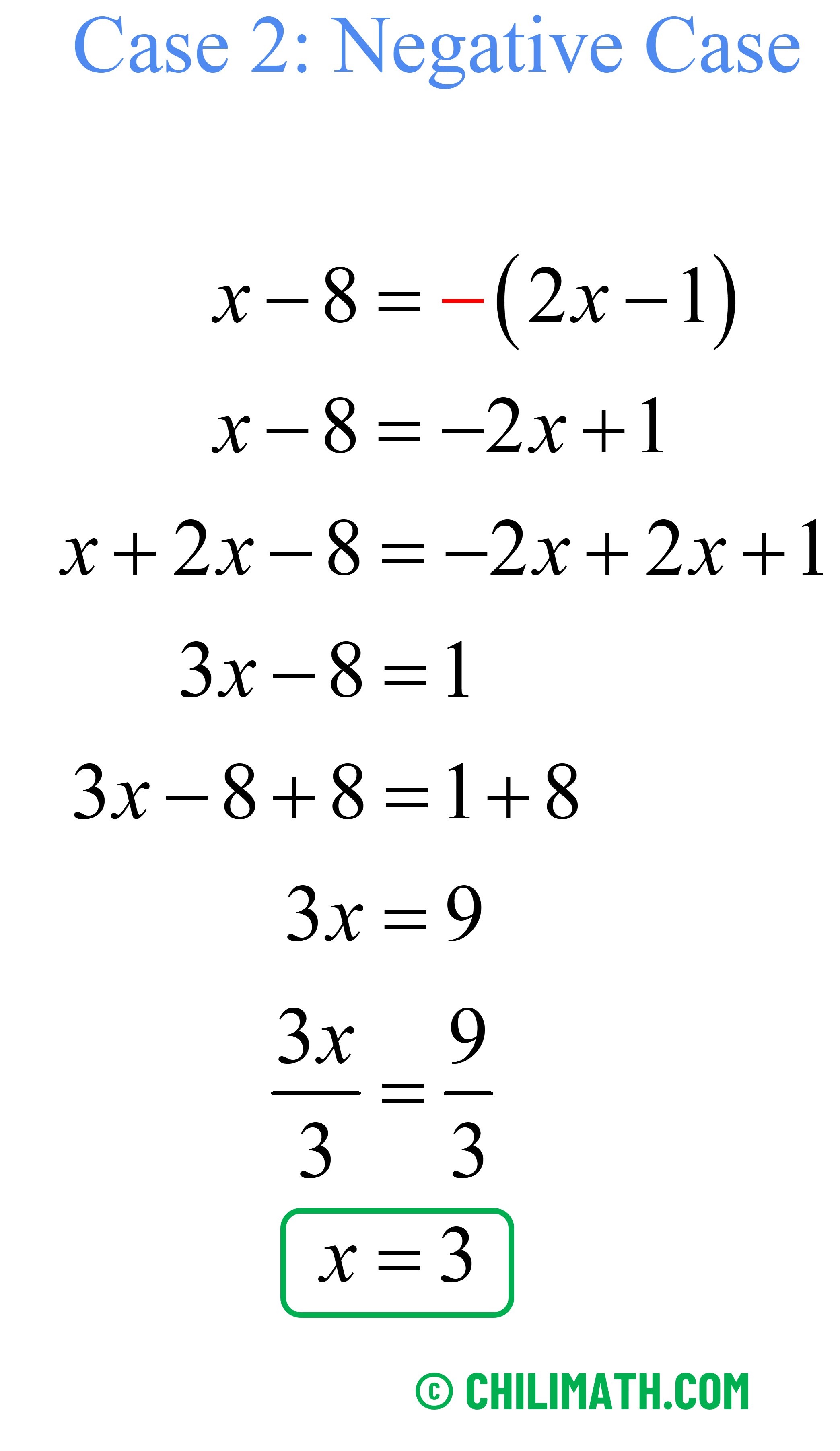
Let’s also validate [latex]x=3[/latex].
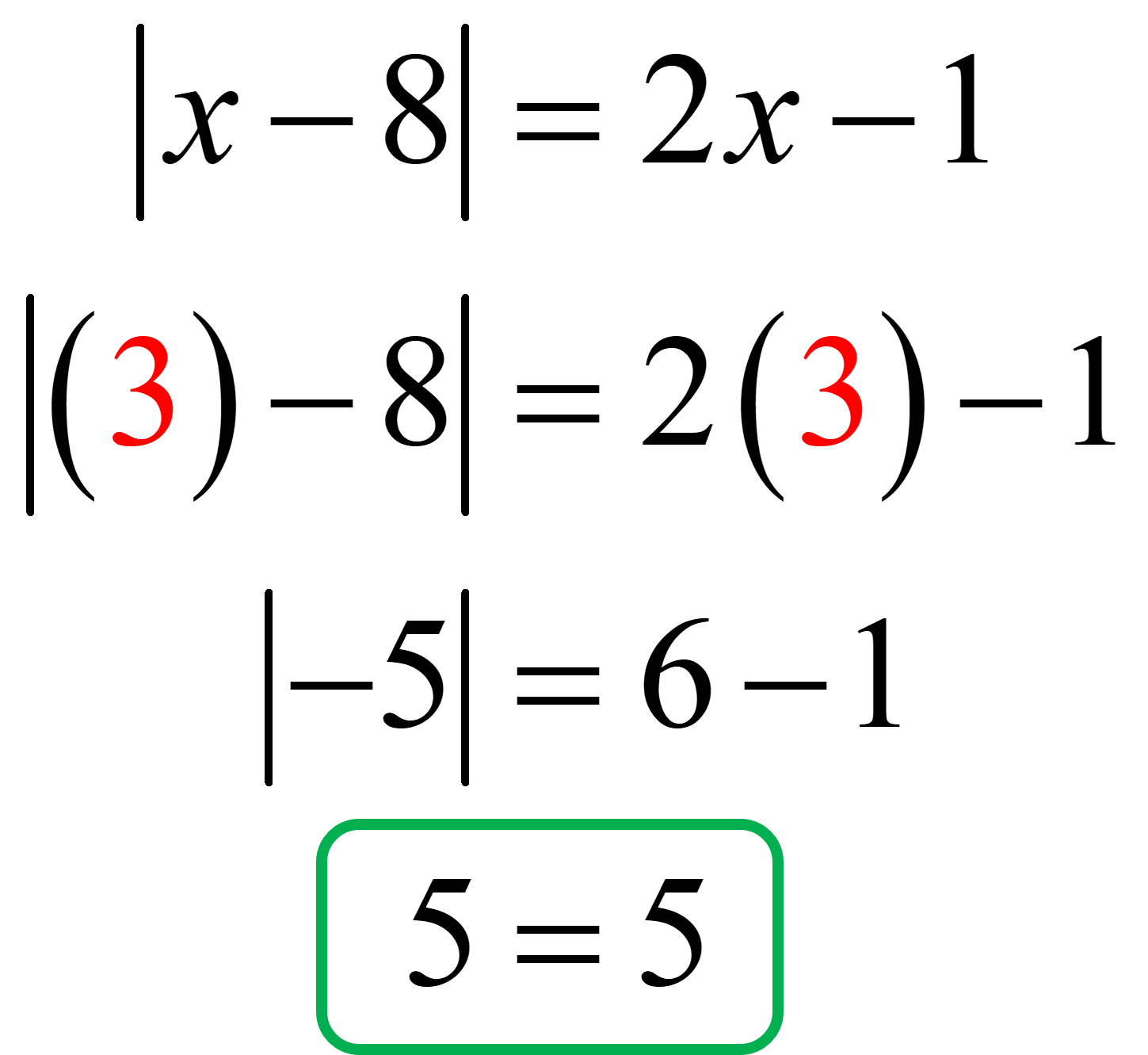
It yields a true statement which means [latex]x=3[/latex] is a solution.
Therefore, the solution set is [latex]\{3\}[/latex].
Problem 9: Solve the absolute value equation below.
[latex]\left| {2x + 5} \right| = x + 7[/latex]
Answer
Break the absolute value equation into two cases of linear equations the solve.
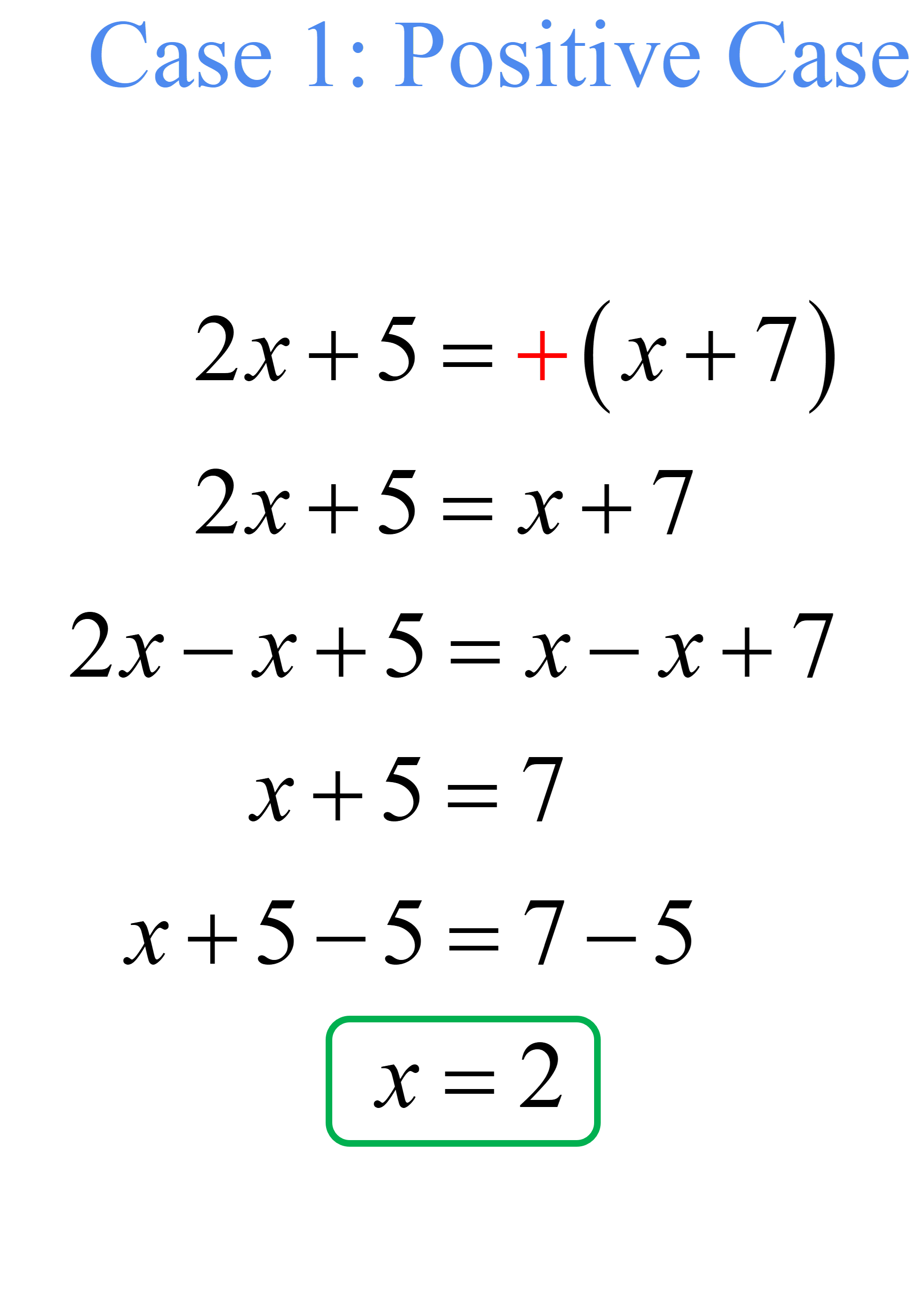
Substitute [latex]x=2[/latex] back into the original absolute value equation to check if it’s true or not. If true, then it is a solution. If false, then it is not.
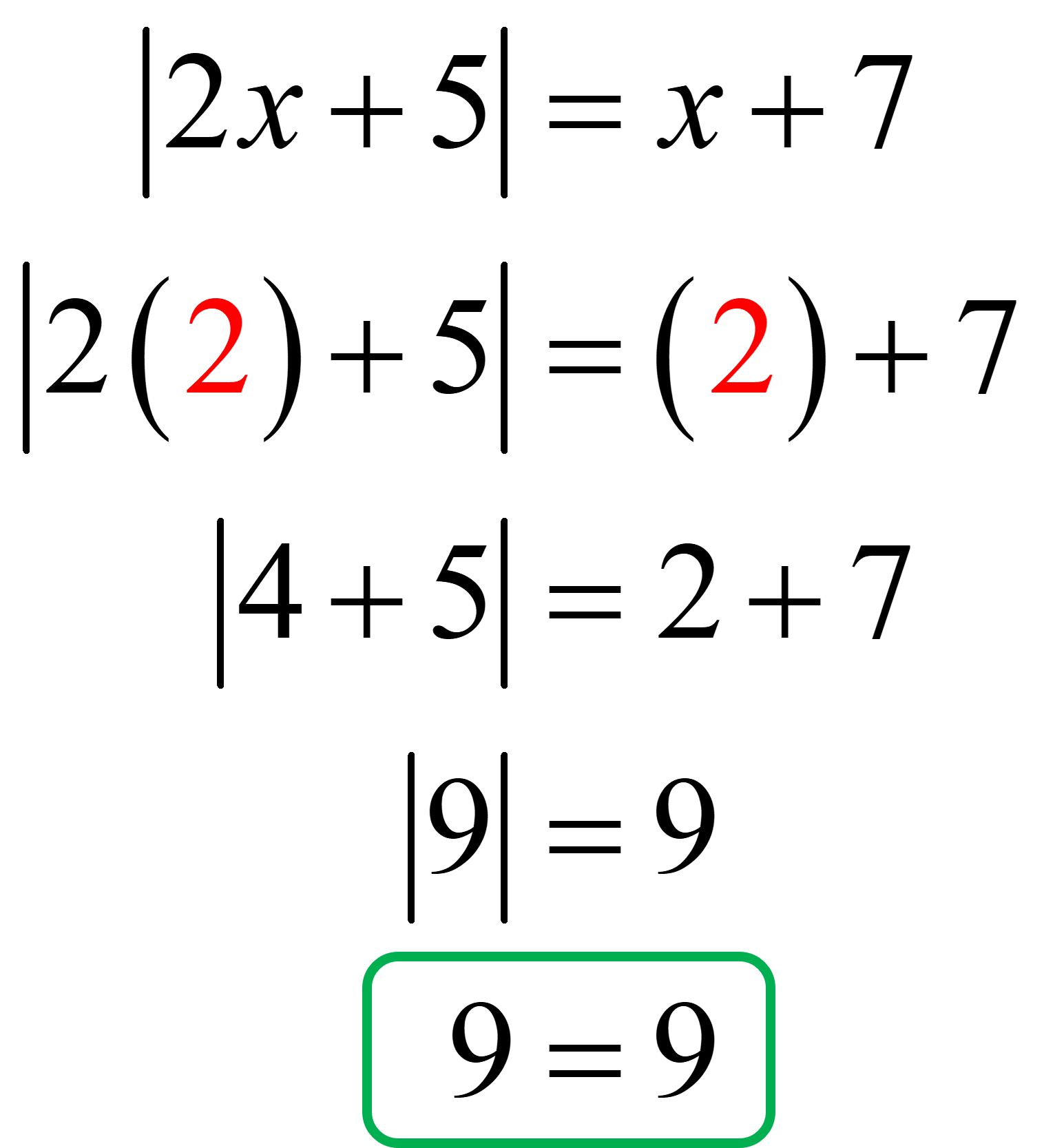
It checks! Therefore, [latex]x=2[/latex] is a solution.
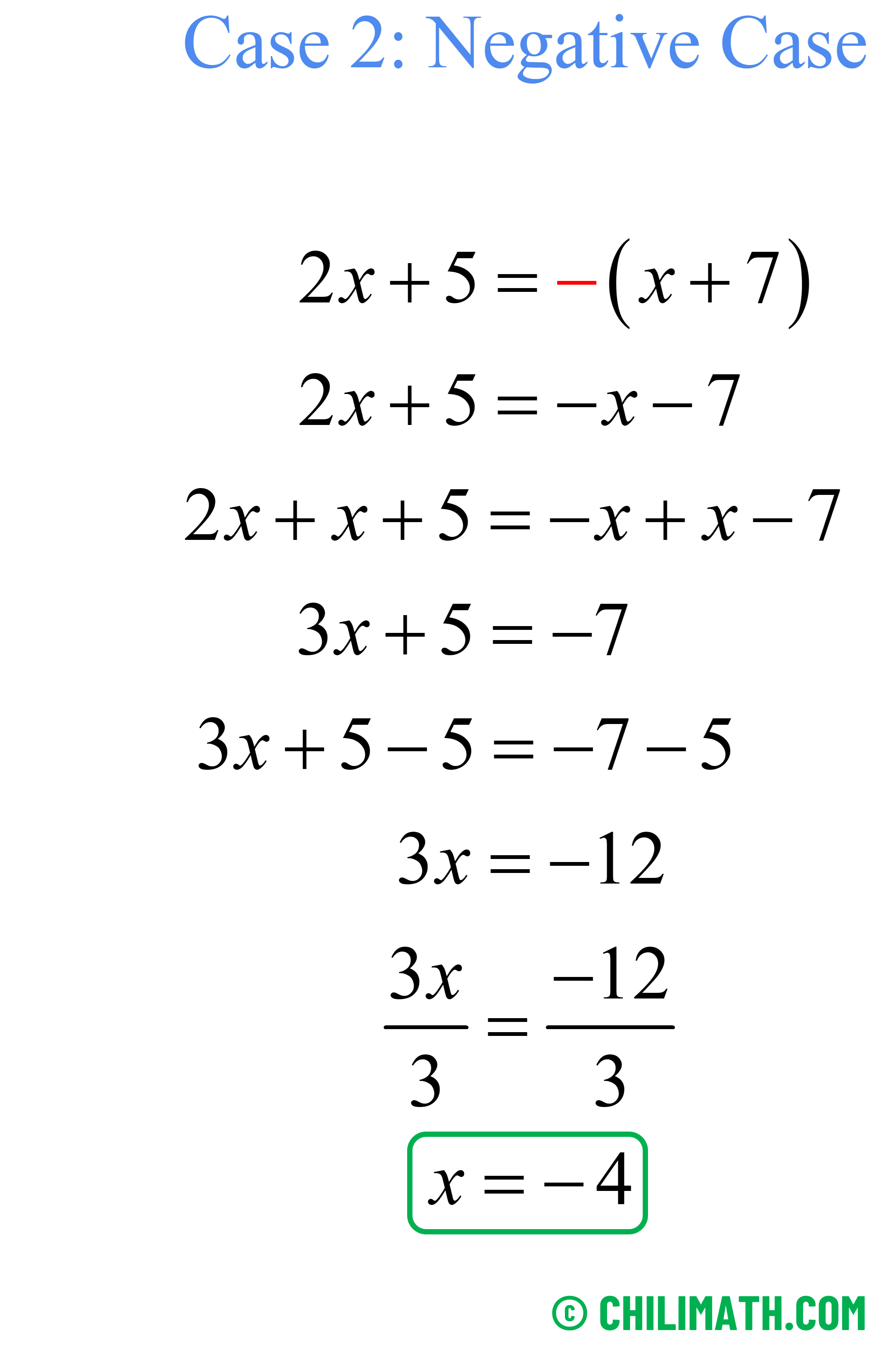
We also validate [latex]x=-4[/latex] using the same procedure as above.
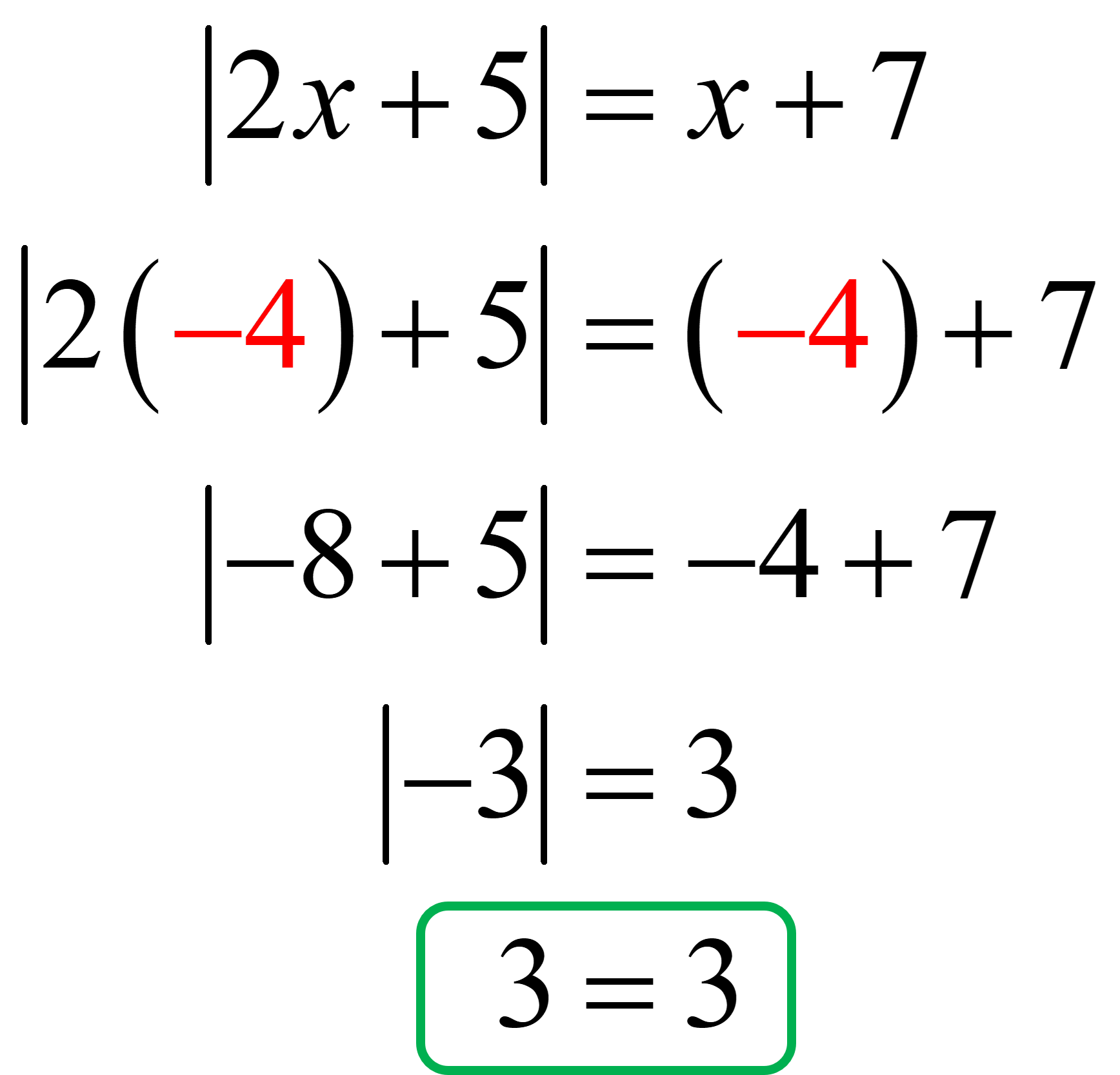
Since it gives a true statement that means [latex]x=-4[/latex] is also a solution.
Therefore, the solution set is [latex]\{ -4,2\}[/latex].
Problem 10: Solve the absolute value equation below.
[latex]\left| {2x + 20} \right| = \left| {3x – 5} \right|[/latex]
Answer
Set up the equations then solve.
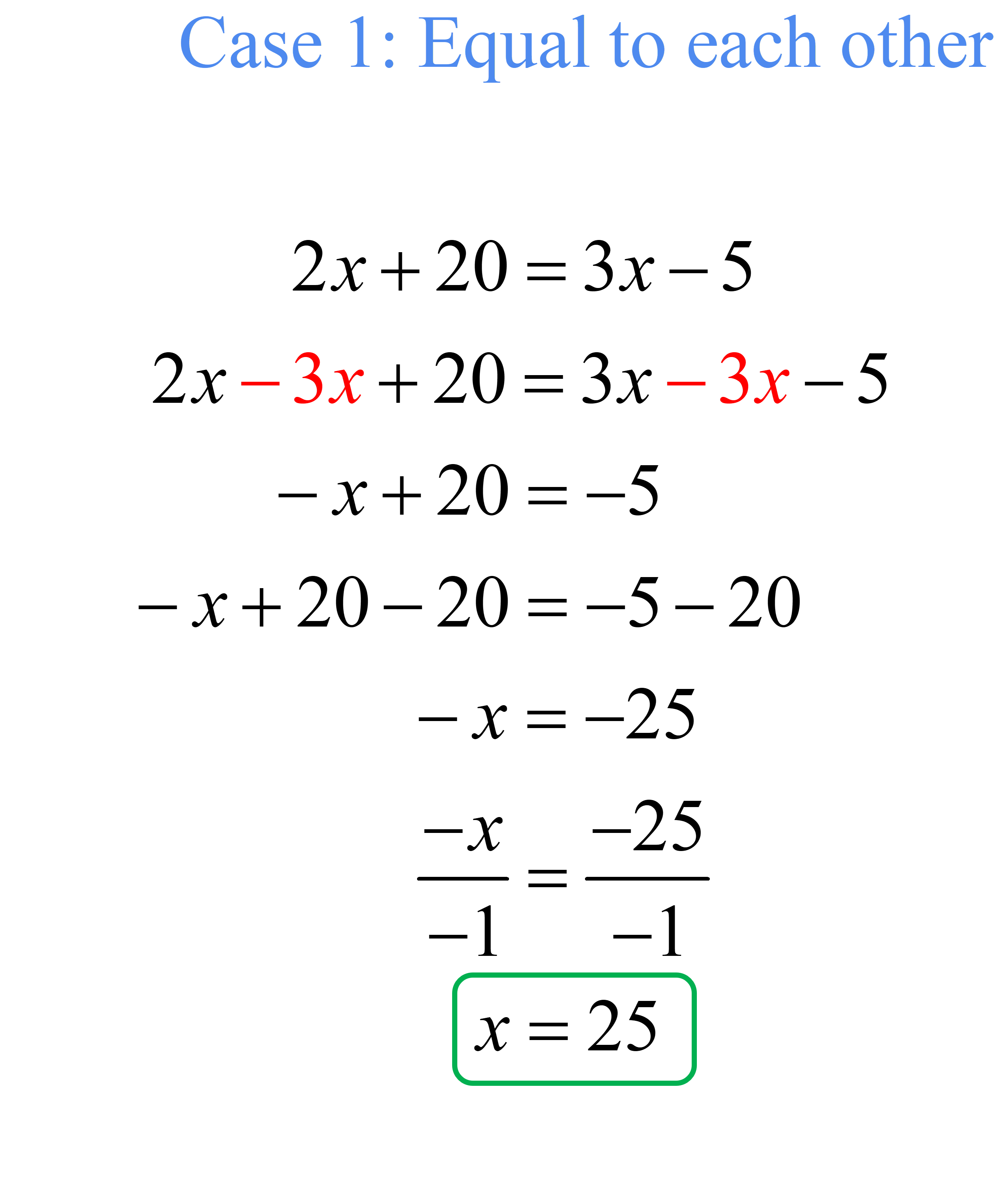
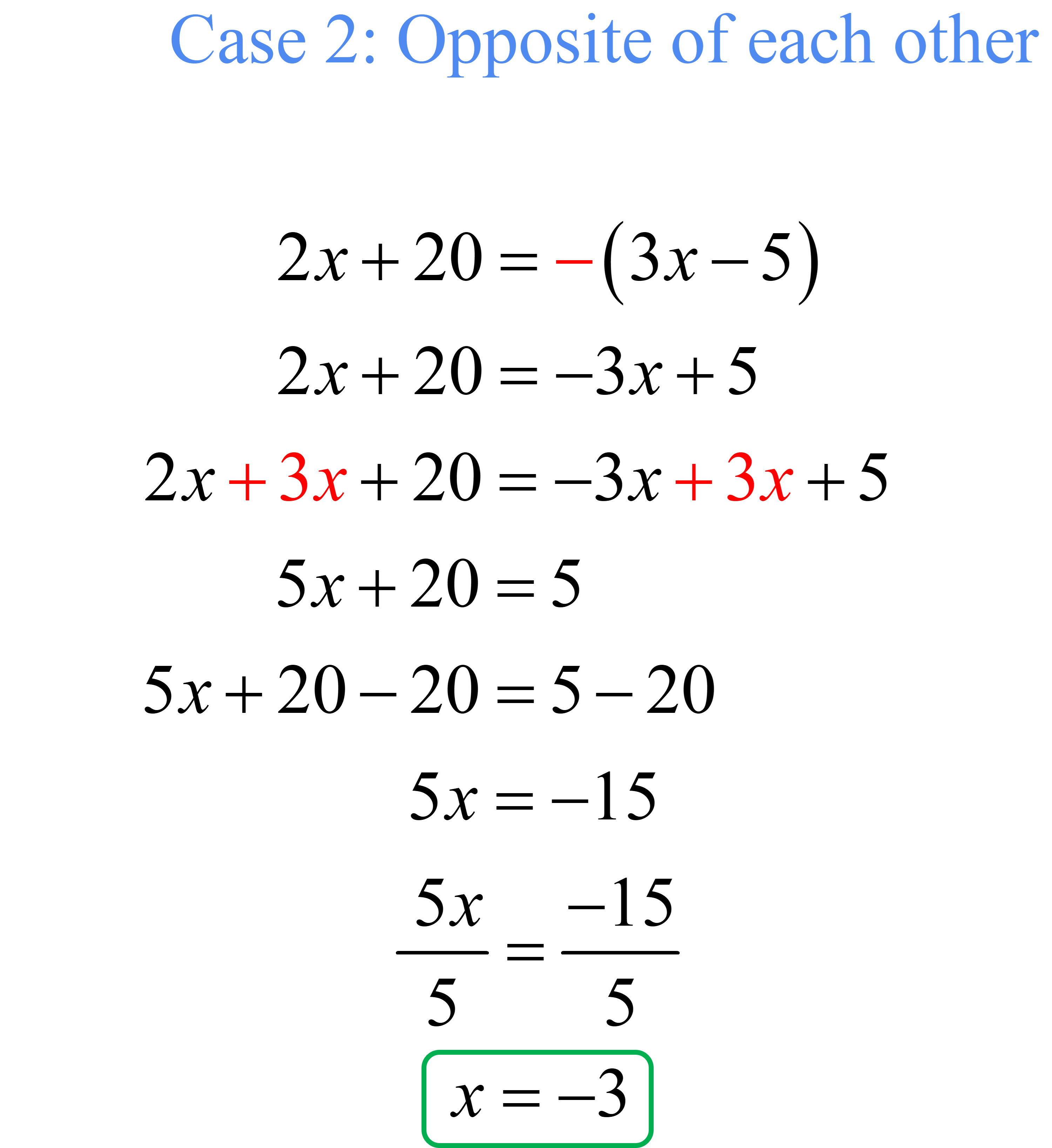
Therefore, the solution set is [latex]\{ -3,25\}[/latex].
Problem 11: Solve the absolute value equation below.
[latex]\left| { – 9x + 10} \right| = \left| {11x} \right|[/latex]
Answer
Set up the absolute value equation into cases then solve.
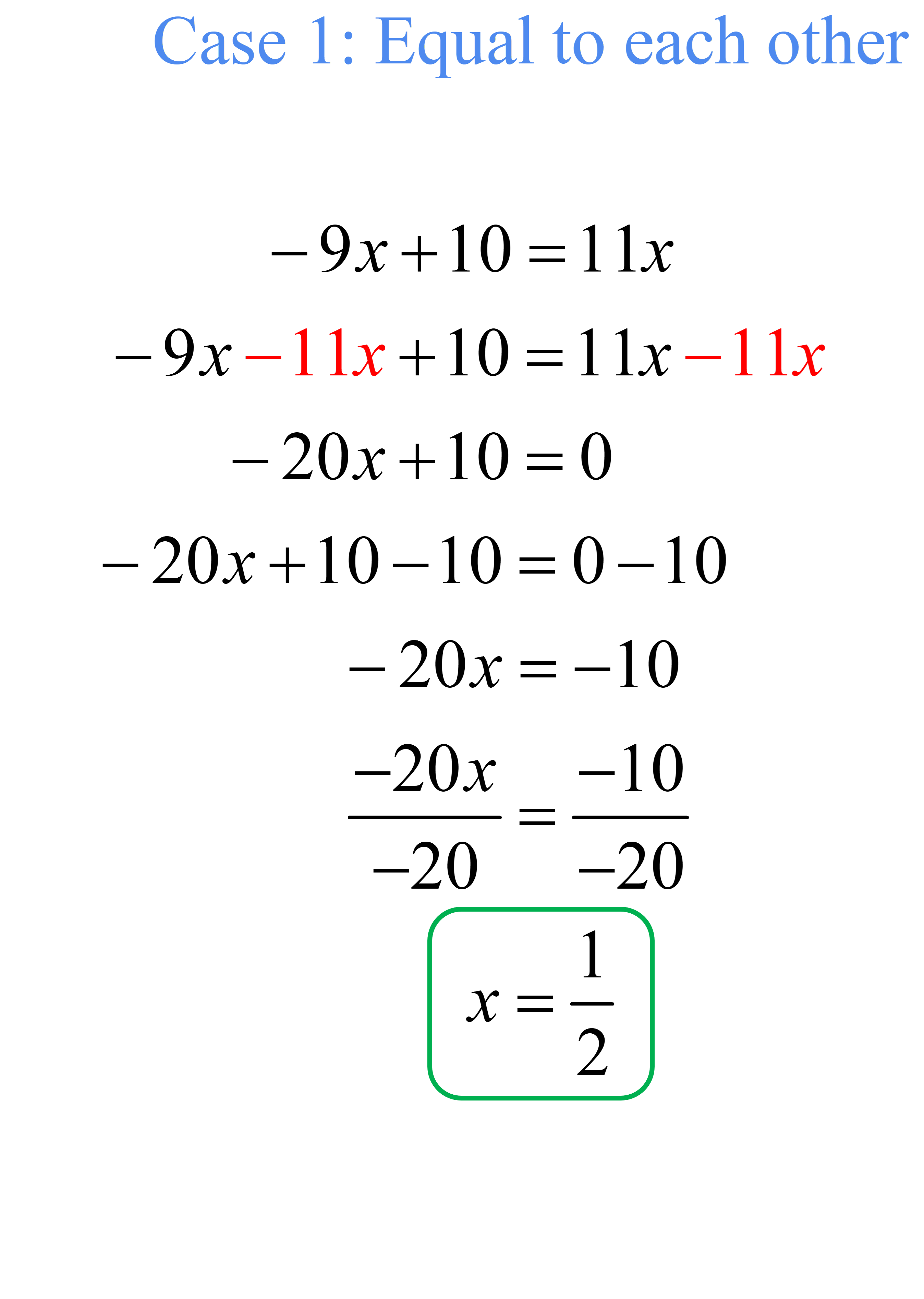
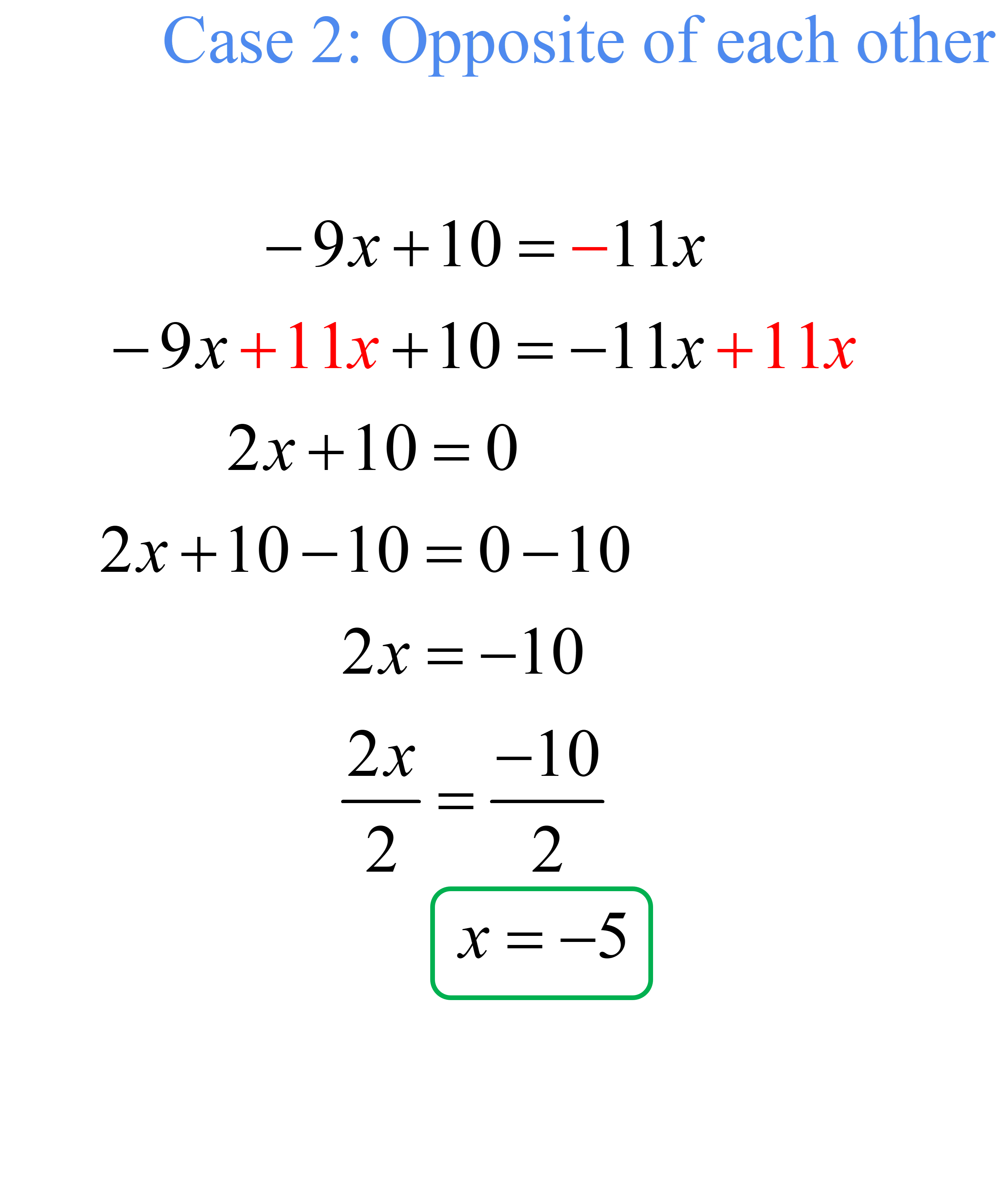
Therefore, the solution set is [latex]\{ -5,1/2\}[/latex].
You may also be interested in these related math lessons or tutorials:
