Area of Trapezoid Formula
A trapezoid is a type of quadrilateral, meaning it has four sides, with one distinctive feature: it has exactly one pair of parallel sides. These parallel sides are referred to as the bases, and we usually label them as [latex]b_1[/latex] and [latex]b_2[/latex]. The perpendicular or vertical distance between these two bases (measured at a right angle) is known as the height [latex]h[/latex] or altitude of the trapezoid.
To calculate the area of a trapezoid we use the following formula:
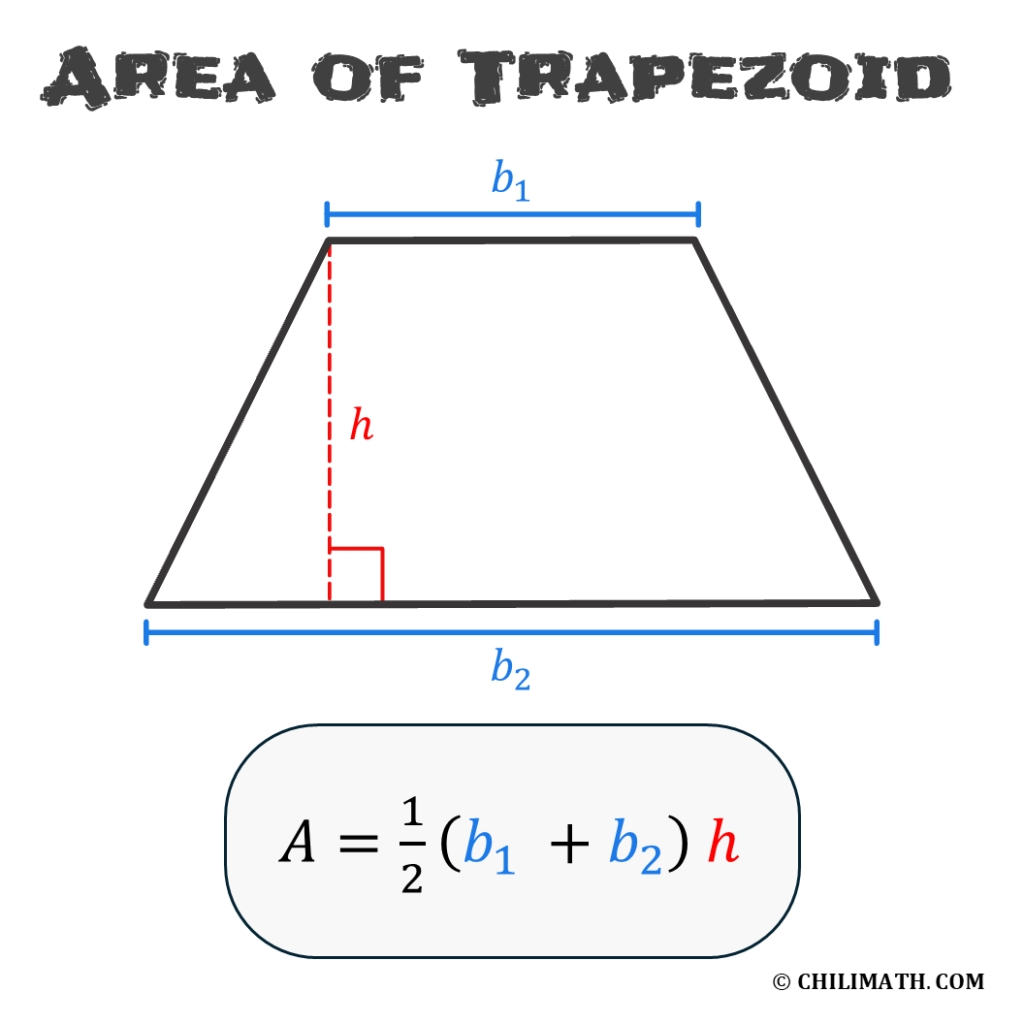
If we rewrite the formula as
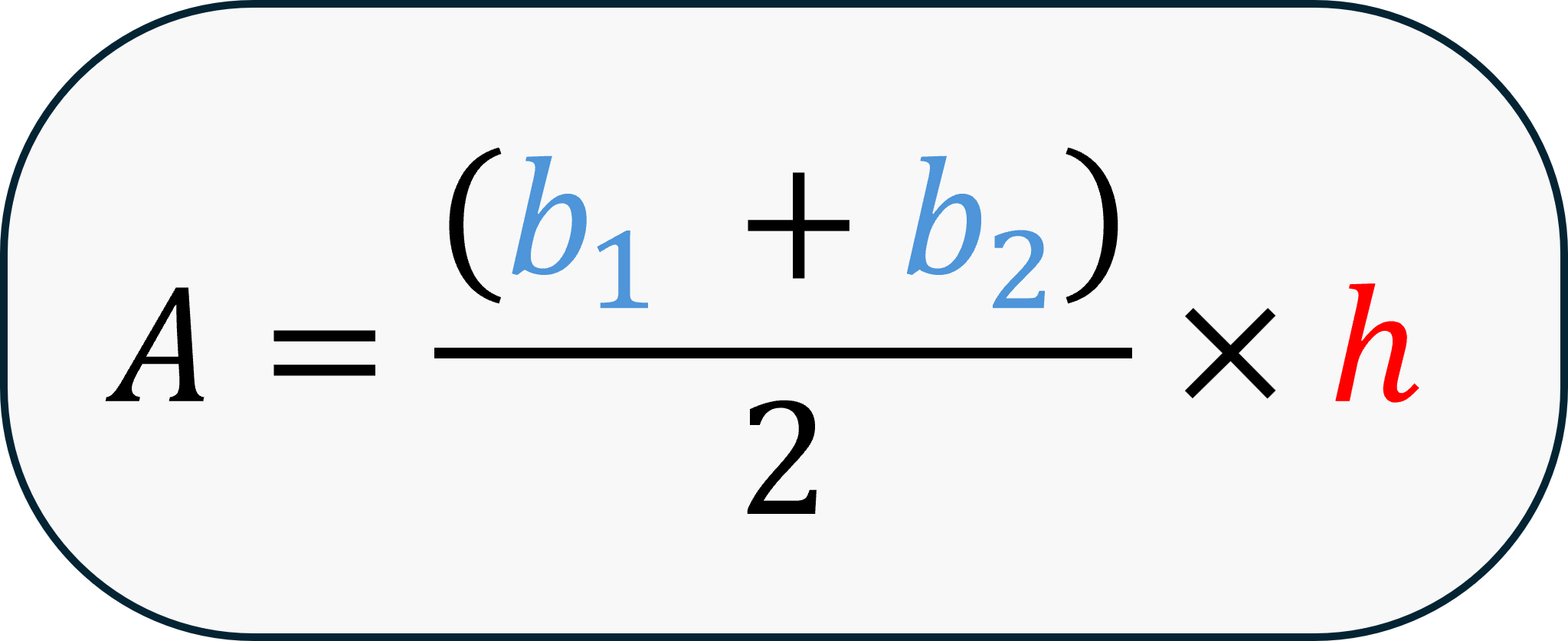
The area of a trapezoid can be calculated by multiplying the height by the average of its two bases.
Examples of Area of Trapezoid Formula
Example 1: Find the area of Trapezoid ABCD.
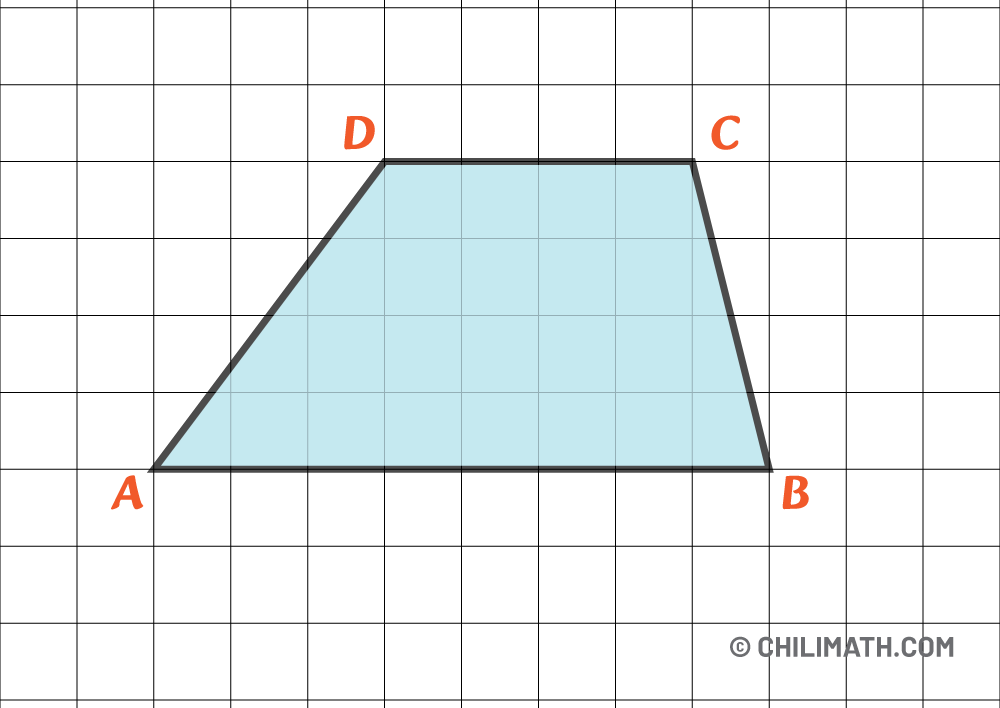
Let’s start by examining the figure. The line segments [latex]\overline{DC}[/latex] and [latex]\overline{AB}[/latex] are parallel, meaning they serve as the bases of the trapezoid. Keep in mind that in a trapezoid, the parallel sides are always considered the bases.
The length of the top base, [latex]\overline{DC}[/latex], is [latex]4[/latex] units, while the length of the bottom base, [latex]\overline{AB}[/latex], is [latex]8[/latex] units. By counting the number of squares from the top base to the bottom base, or vice versa, we find that the height of the trapezoid is [latex]4[/latex] units.
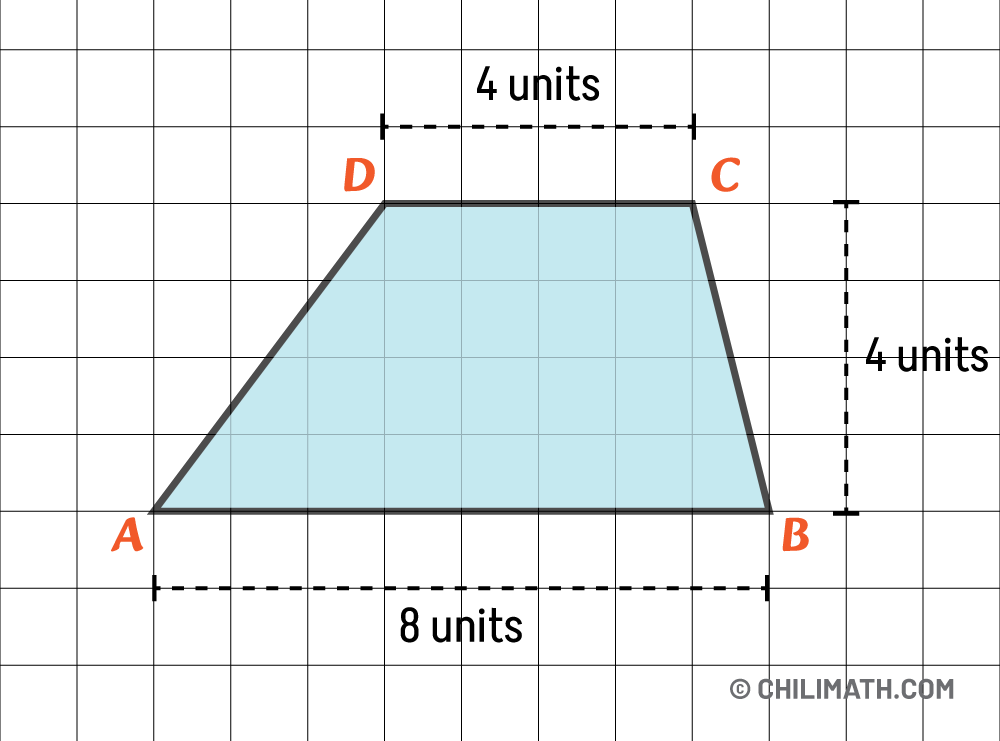
If we let the top base as [latex]{b_1}[/latex], the bottom base as [latex]{b_2}[/latex] and height as [latex]h[/latex], we can now perform the substitutions into the formula:
\begin{align*} & {b_1} = 4 \\ & {b_2} = 8 \\ & h = 4 \\ \\ A &= {1 \over 2}\left( {{b_1} + {b_2}} \right)h \\ & = {1 \over 2}\left( {4 + 8} \right) \times 4 \\ & = {1 \over 2}\left( {12} \right) \times 4 \\ & = 6 \times 4 \\ A &= 24 \end{align*}Therefore, the area of the trapezoid is [latex]24[/latex] square units.
Example 2: Find the area of Trapezoid WXYZ.
If we carefully count the number of squares along the horizontal side of the top base, we find that it’s [latex]8[/latex] units long, while the bottom base measures [latex]10[/latex] units. Now, if we count the squares along the vertical line connecting the two bases, the height comes out to be [latex]5[/latex] units.
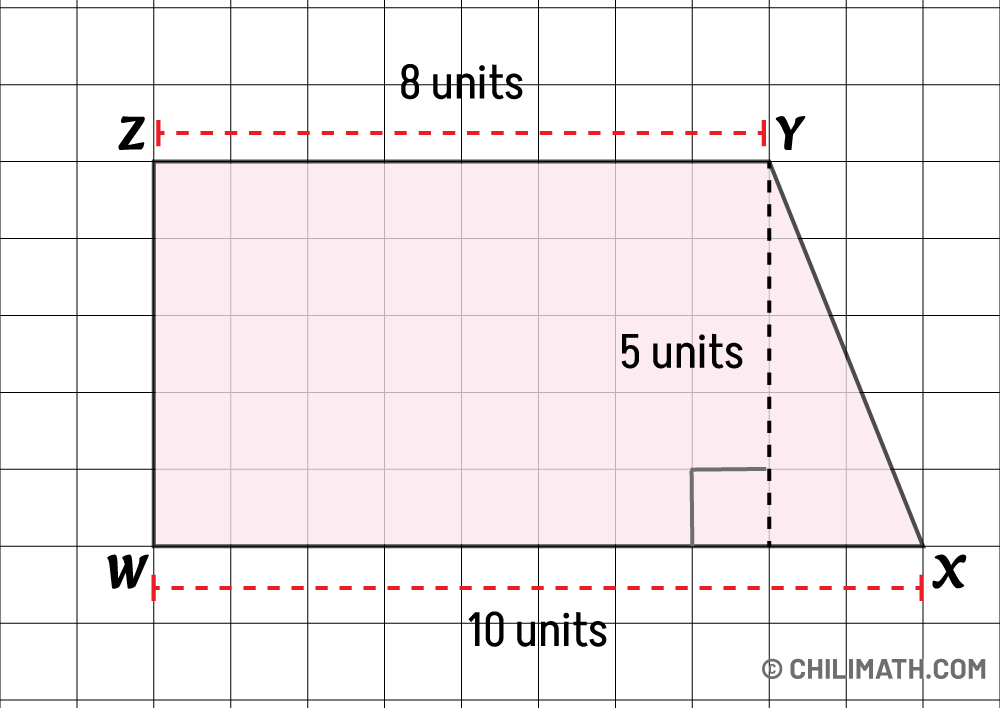
We substitute this information into the formula to calculate the area of the trapezoid.
\begin{align*} & {b_1} = 8 \\ & {b_2} = 10 \\ & h = 5 \\ \\ A &= {1 \over 2}\left( {{b_1} + {b_2}} \right)h \\ & = {1 \over 2}\left( {8 + 10} \right) \times 5 \\ & = {1 \over 2}\left( {18} \right) \times 5 \\ & = 9 \times 5 \\ A &= 45 \end{align*}Therefore, the area of the trapezoid is [latex]45[/latex] [latex]\text{unit}^2[/latex].
Example 3: A trapezoid has an area of [latex]120[/latex] [latex]\text{ft}^2[/latex]. The lengths of the two bases are [latex]8[/latex] [latex]\text{ft}[/latex] and [latex]12[/latex] [latex]\text{ft}[/latex]. Find the height of the trapezoid.
We know the area of the trapezoid to be [latex]120[/latex] [latex]\text{ft}^2[/latex]. That means
[latex]A = 120[/latex] [latex]\text{ft}^2[/latex]
Also, the two bases have the following lengths:
\begin{align*} & {b_1} = 8 \,\text{ft} \\ & {b_2} = 12 \,\text{ft} \end{align*}Let’s substitute the values into the formula then solve for the height [latex]\color{red}h[/latex].
\begin{align*} & A = 120 \\ & {b_1} = 8 \\ & {b_2} = 12 \\ & {\color{red}h} = ? \\ \\ A &= {1 \over 2}\left( {{b_1} + {b_2}} \right)h \\ 120 &= {1 \over 2}\left( {8 + 12} \right)h \\ 120 &= {1 \over 2}\left( {20} \right) \times h \\ 120 &= 10h \\ 12 &= h \end{align*}Therefore, the height of the trapezoid is [latex]12[/latex] [latex]\text{ft}[/latex].
Example 4: A trapezoid has an area of [latex]390[/latex] [latex]\text{cm}^2[/latex]. If one of the bases of the trapezoid measures [latex]24[/latex] [latex]\text{cm}[/latex] and its height is [latex]15[/latex] [latex]\text{cm}[/latex], what is the length of the other base?
This problem is quite similar to Example #3. We’re given three values in the equation, and our goal is to solve for the last variable, which in this case is the other base. If we let the given base be [latex]{b_1} = 24[/latex], then our task is to find the other base, [latex]{b_2}[/latex].
So these are the given information by far.
\begin{align*} & A = 390\, \text{cm}^2 \\ & h = 15 \, \text{cm} \\ & {b_1} = 24\, \text{cm} \end{align*}That means, we want to find [latex]b_2[/latex].
[latex]b_2=?[/latex]
Solving for other base:
\begin{align*} & A = {1 \over 2}\left( {{b_1} + {b_2}} \right)h \\ \\ & 390 = {1 \over 2}\left( {24 + {b_2}} \right)\left( {15} \right) \\ \\ & 780 = \left( {24 + {b_2}} \right)\left( {15} \right) \\ \\ & {{780} \over {15}} = {{\left( {24 + {b_2}} \right)\left( {15} \right)} \over {15}} \\ \\ & 52 = 24 + {b_2} \\ \\ & 52 – 24 = 24 – 24 + {b_2} \\ \\ & 28 = {b_2} \end{align*}Therefore, the length of the other base is [latex]28[/latex] [latex]\text{cm}[/latex].
You might also like these tutorials: