Angles

An angle is formed by two rays that share a common endpoint, known as the vertex. The rays are referred to as the sides of the angle.

The sides of an angle are also called the arms of an angle. They are the two straight lines (or rays) that form the angle. These arms originate from a common point, known as the vertex of the angle.

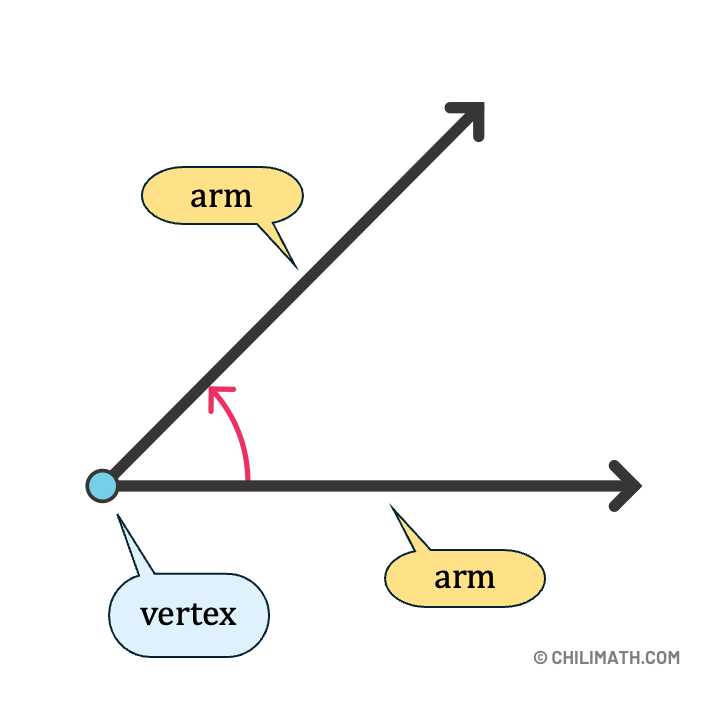
Referring to the two arms or sides of an angle, one ray is stationary or fixed (called the initial side), while the other ray rotates to create the angle (known as the terminal side).

Let’s discuss the different ways to name an angle. Typically, there are three methods used to name an angle to ensure there’s no confusion. Consider the diagram below.

We can name the angle above in three various ways:

1. Name the angle using its vertex: \(\angle\)A
2. Name the angle using three points but making sure the vertex is in the middle: \(\angle\)CAB or \(\angle\)BAC
3. Name the angle using the number inside the angle: \(\angle\)1

We need to be particularly careful when naming angles when two or more angles share the same vertex. In this case, simply using the vertex to name the angles isn’t enough to clearly identify which angle we’re referring to. Take a look at the diagram below for clarification.

Notice, that \(\angle\)E can mean any of the three angles above. That is,

• \(\angle\)E may refer to \(\angle\)1 or \(\angle\)MEF
• \(\angle\)E may refer to \(\angle\)2 or \(\angle\)GEM
• \(\angle\)E may refer to \(\angle\)GEF

When we have two or more angles that share the same vertex, it’s best to use a three-letter designation to clearly specify which angle we’re referring to.

• \(\angle\)1 is the same as \(\angle\)MEF or \(\angle\)FEM
• \(\angle\)2 is the same as \(\angle\)GEM or \(\angle\)MEG
• the angle with the largest amount of rotation is \(\angle\)GEF or \(\angle\)FEG

To measure angles, we use a protractor. The unit for measuring angles is called degrees, and it’s represented by a small circle in the upper right corner of the number. If we have an angle that measures \(34\) degrees, we write it as \(34^\circ\).

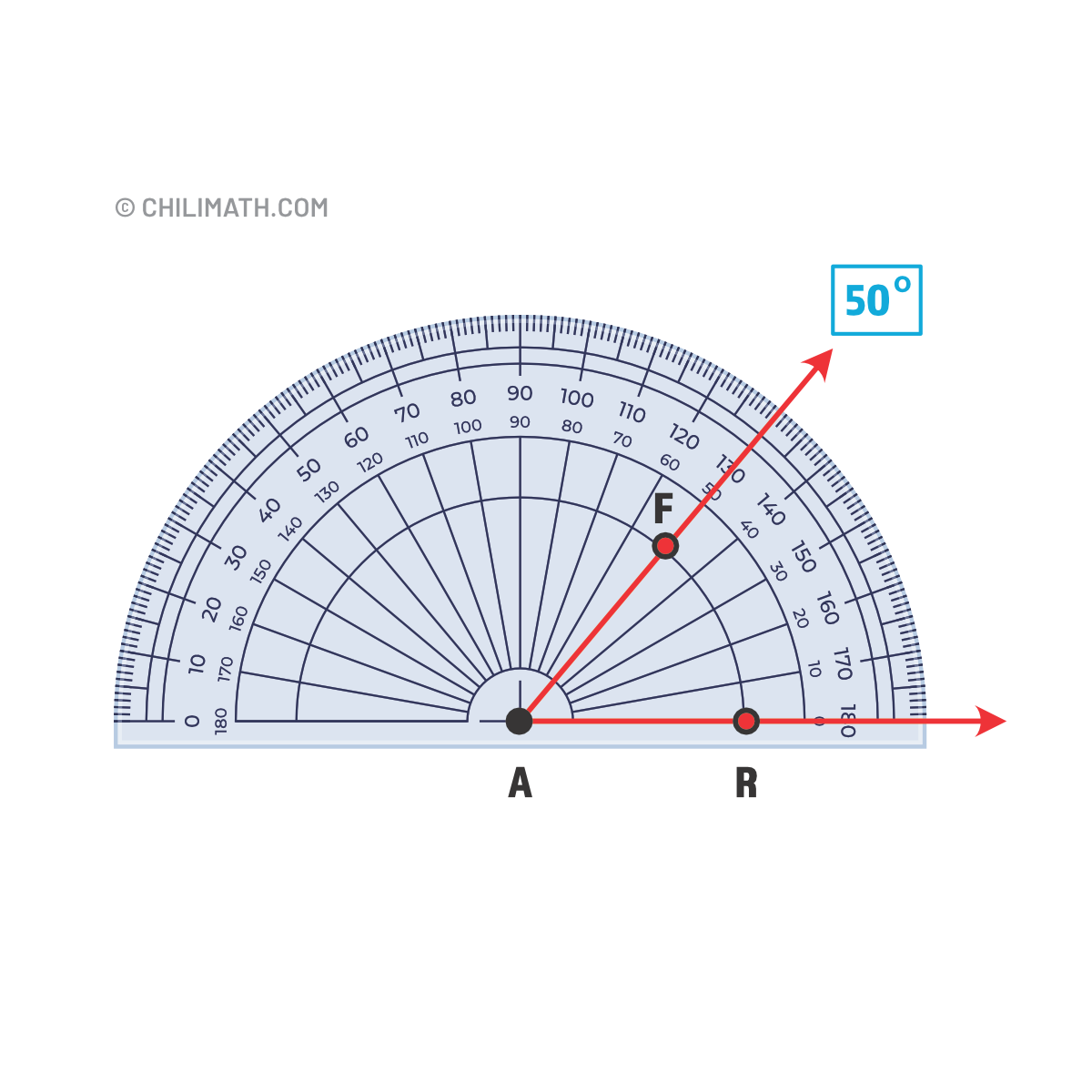
Let’s practice using a protractor to measure the following angles.

• What is the measure of \(\angle\)FAR?

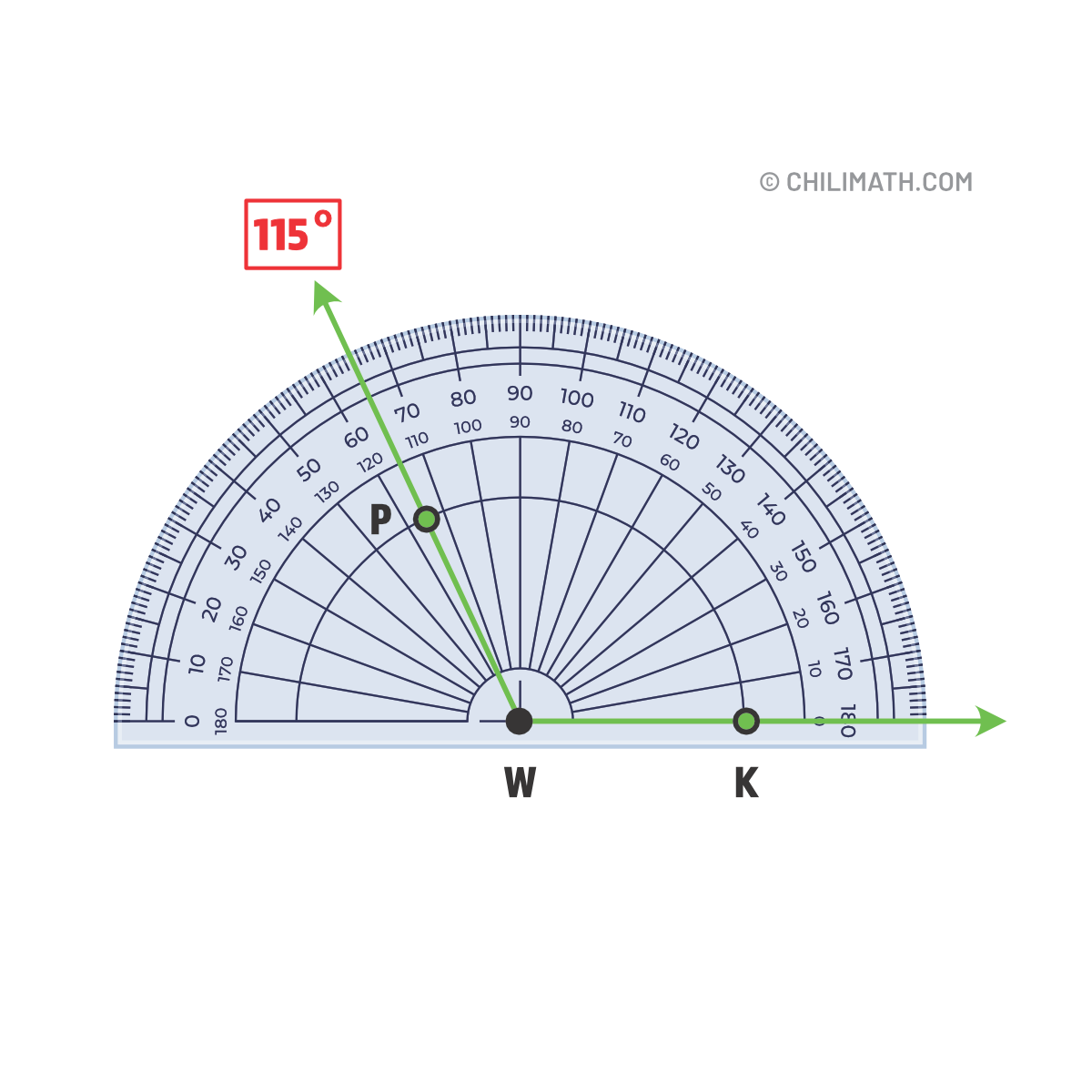
• What is the measure of \(\angle\)PWK?

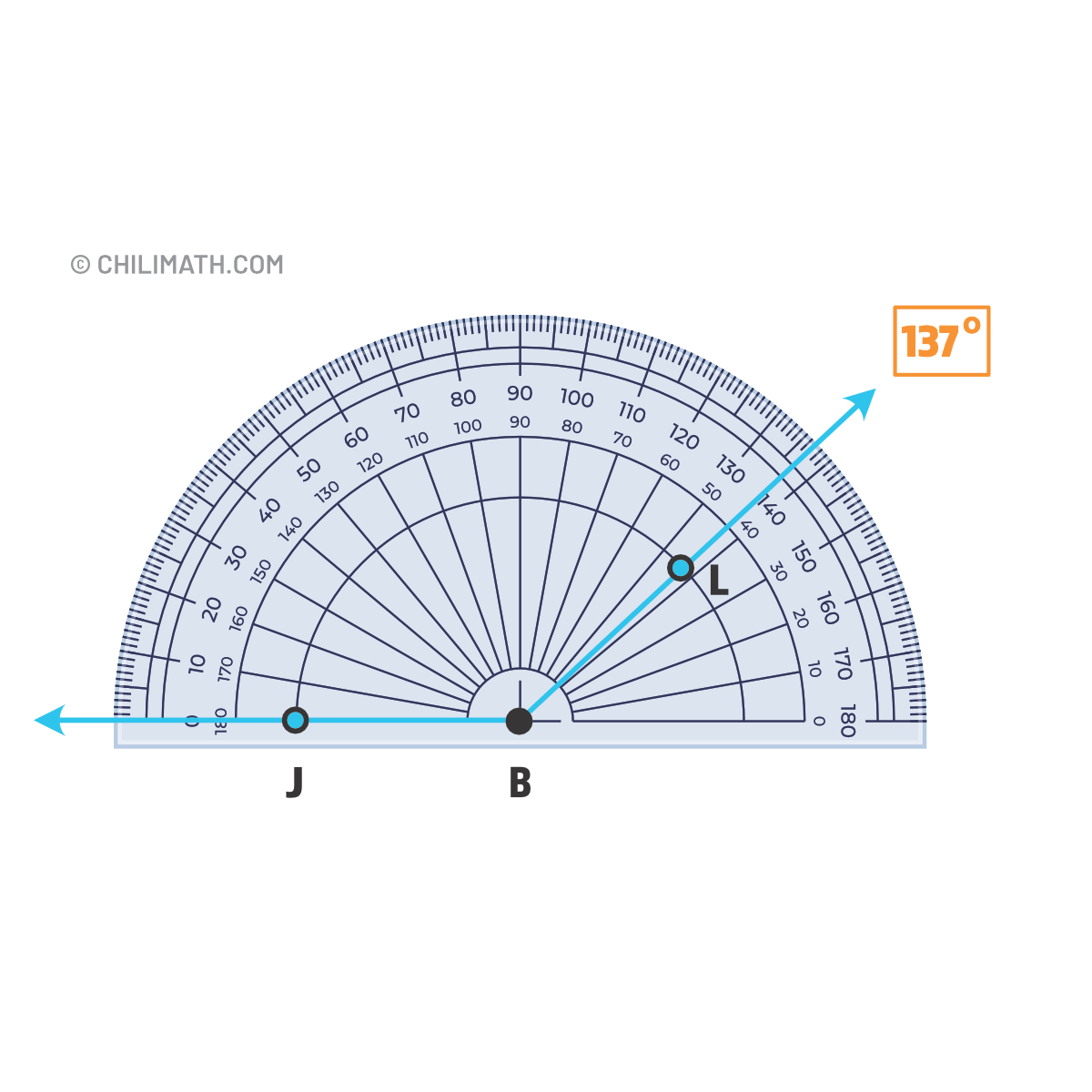
What is the measure of \(\angle\)JBL?

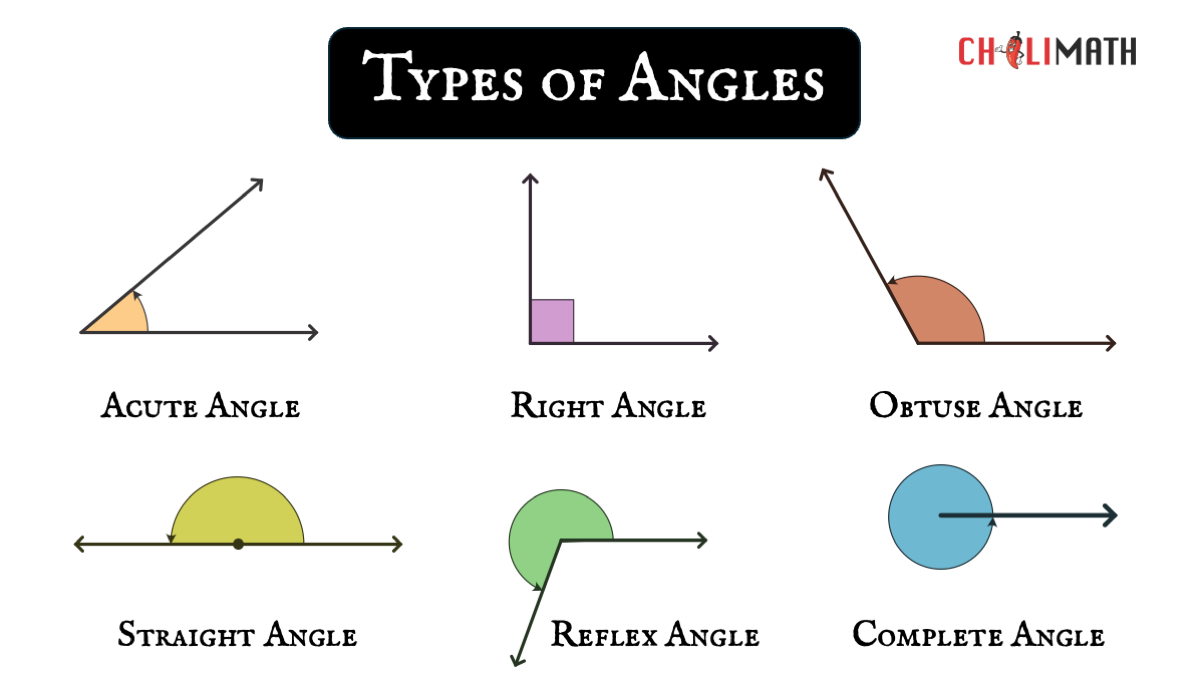
Angles can also be classified based on their angle measures. Here are the main types of angles.

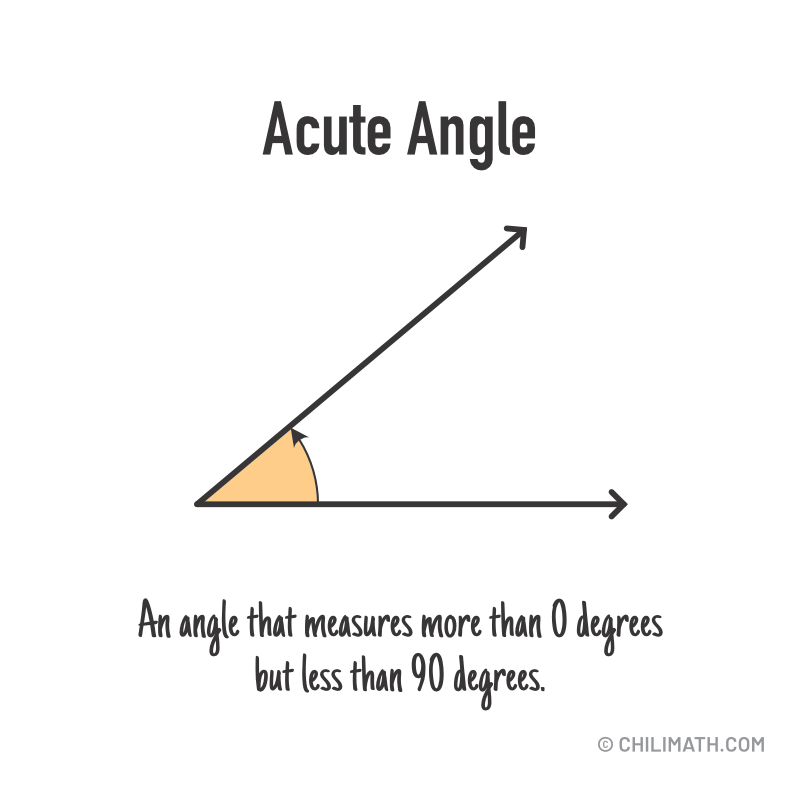
1) Acute Angle – an angle that measures more than zero degrees but less than 90 degrees.

2) Right Angle – an angle that measures exactly 90 degrees.

3) Obtuse Angle – an angle that measures more than 90 degrees but less than 180 degrees.

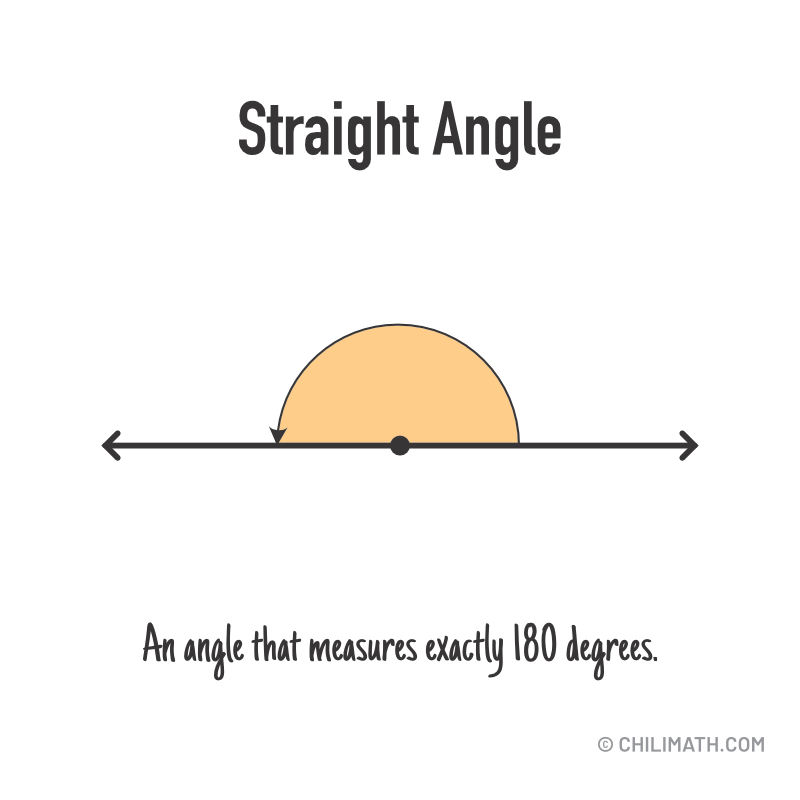
4) Straight Angle – an angle that measures exactly 180 degrees.

5) Reflex Angle – an angle that measures more than 180 degrees but less than 360 degrees.

6) Complete Angle or Full Rotation – an angle that measures exactly 360 degrees.

Here’s a brief summary of the various types of angles for quick reference.

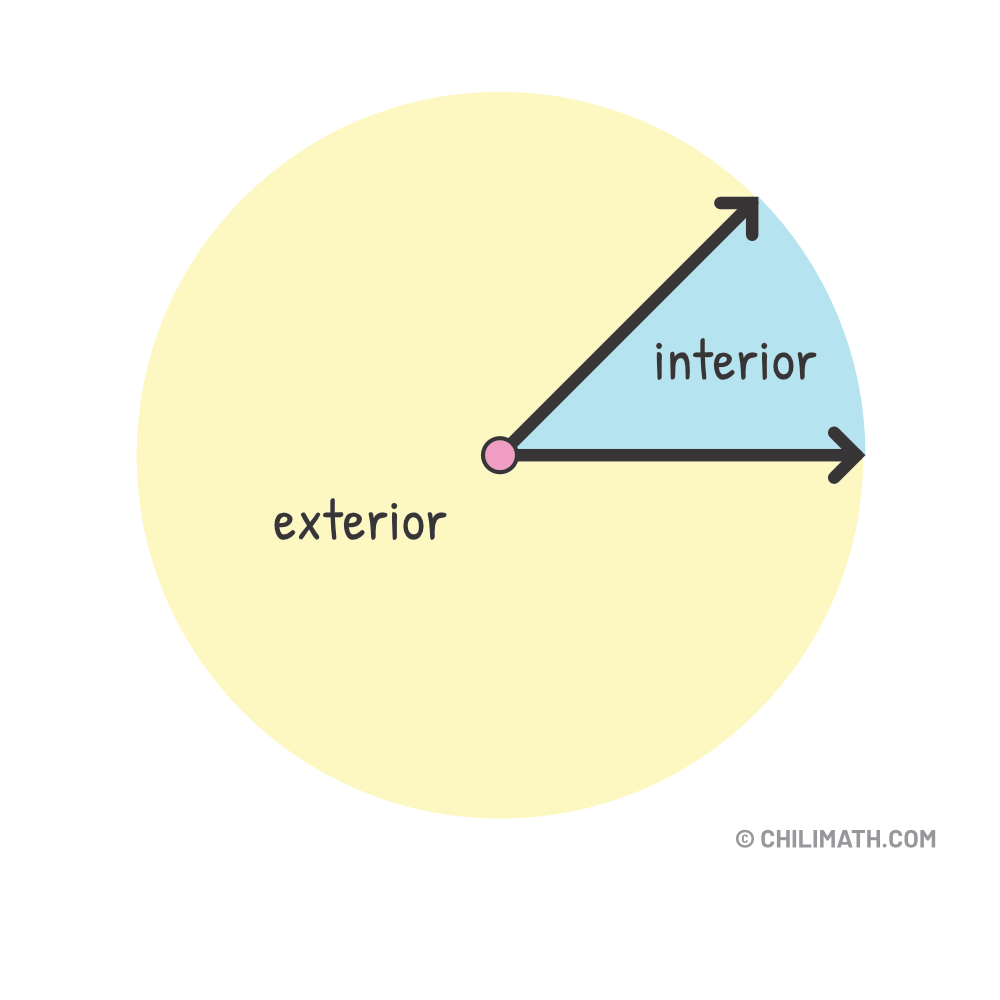
Sometimes, we want to know if the points are in the interior or exterior of angles. This concept is useful in defining other concepts regarding angles.

• Interior points of an angle are those located between the two rays forming the angle, within its boundaries, but not on the rays themselves.
• Exterior points of an angle are those that lie outside the region between the two rays forming the angle. These points are neither within the “opening” of the angle nor on the rays themselves.

Now, we can define adjacent angles using the concept of interior and exterior points.

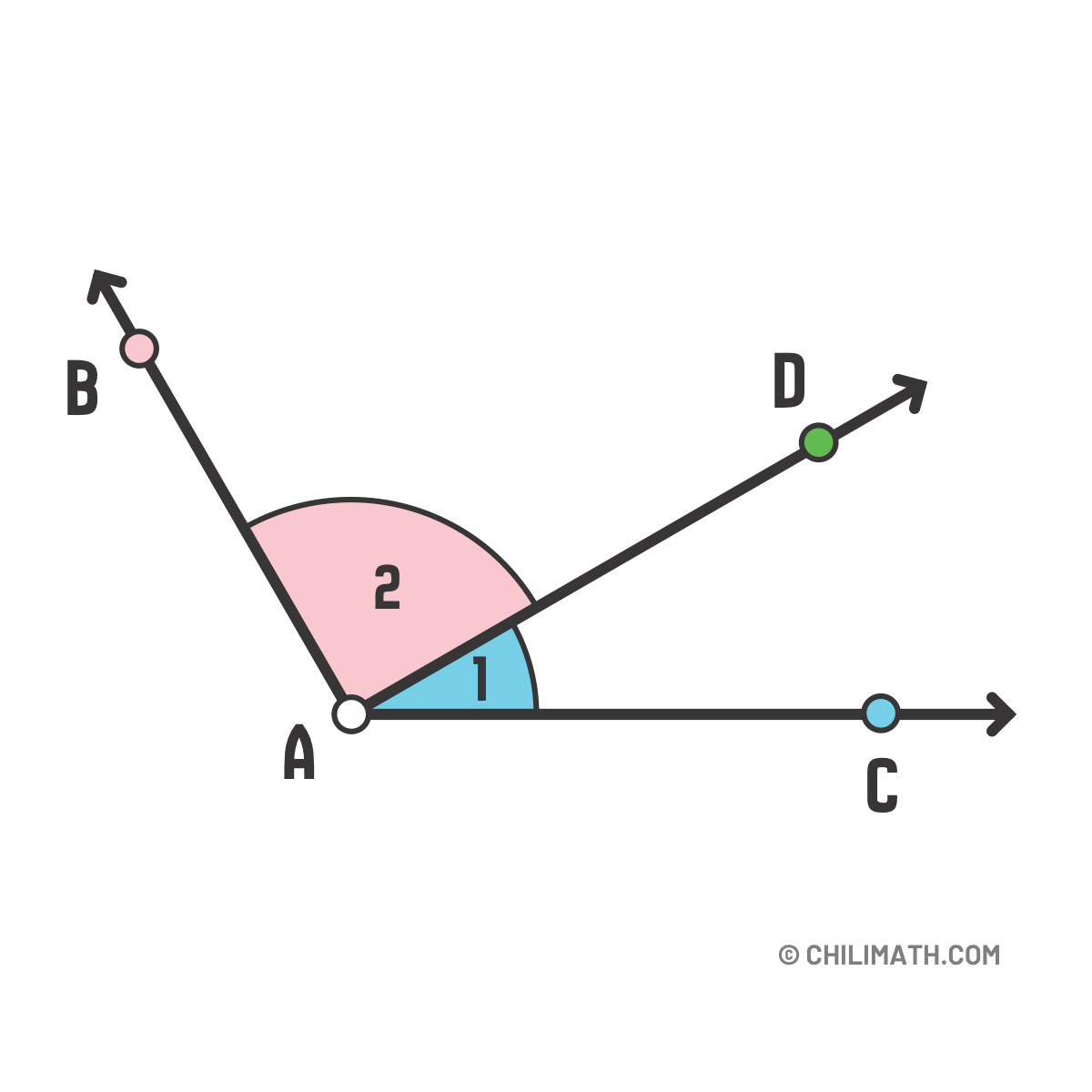
Referring to the diagram above, \(\angle\)BAD and \(\angle\)DAC are considered adjacent angles because they share a common vertex at point \(A\) and a common side, \(\overrightarrow{\rm AD}\), but they have no common interior points.