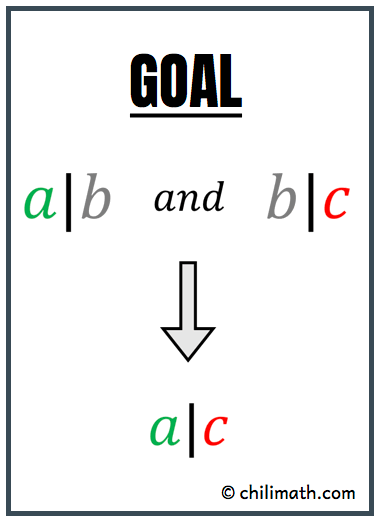
Prove: If [latex]a|b[/latex] and [latex]b|c[/latex], then [latex]a|c[/latex].
This theorem is usually written as follows:
Theorem: Let [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] be integers with [latex]a \ne 0[/latex] and [latex]b \ne 0[/latex]. If [latex]a|b[/latex] and [latex]b|c[/latex], then [latex]a|c[/latex].
In order to prove this statement, we first need to understand what the math notation [latex]\color{red}a|b[/latex] implies.
I have a separate lesson discussing the meaning of [latex]a|b[/latex].
To review, the math notation [latex]a|b[/latex] is read as “[latex]a[/latex] divides [latex]b[/latex] “. The assumption is that both [latex]a[/latex] and [latex]b[/latex] are integers but [latex]a[/latex] doesn’t equal zero, [latex]a \ne 0[/latex]. In addition, the vertical bar in [latex]a|b[/latex] is called pipe.
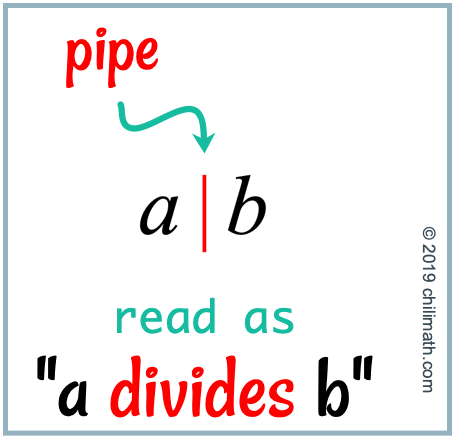
As it stands, the notation [latex]a|b[/latex] is not useful to us because in its current form, there’s no way that we can algebraically manipulate it. We must convert it in an equation form.
Here’s the thing, [latex]a|b[/latex] can be written in the equation as [latex]b = ar[/latex] where [latex]r[/latex] is an integer.
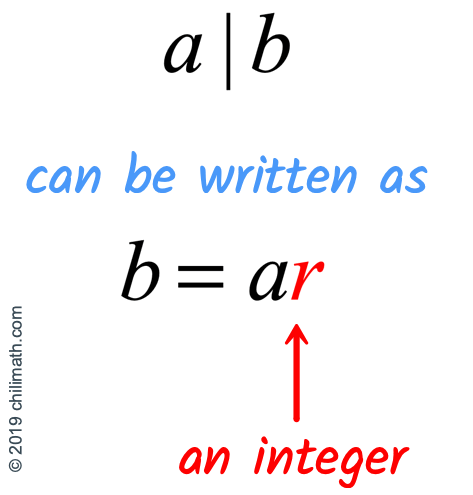
For example, in [latex]2|10[/latex], we know that [latex]2[/latex] evenly divides [latex]10[/latex]. That means there is an integer when multiplied to [latex]2[/latex] gives a product of [latex]10[/latex].
What could that number be? It is [latex]\color{red}5[/latex] since [latex]2 \times 5 = 10[/latex].
Thus, we say [latex]2|10[/latex] implies [latex]10 = 2\left( 5 \right)[/latex]
BRAINSTORM BEFORE WRITING THE PROOF

Note: The purpose of brainstorming in writing proof is for us to understand what the theorem is trying to convey; and gather enough information to connect the dots, which will be used to bridge the hypothesis and the conclusion.
Since we are using the method of direct proof, we want to show that we can manipulate the hypothesis to arrive at the conclusion.
Hypothesis: [latex]a[/latex] divides [latex]b[/latex] AND [latex]b[/latex] divides [latex]c[/latex]
Conclusion: [latex]a[/latex] divides [latex]c[/latex]
Now, let’s express each notation into an equation. We hope that by doing so will reveal an opportunity so we can proceed with our line of reasoning.
| Notations | Equations | Notes |
|---|---|---|
| [latex]a|b[/latex] | [latex]b = am[/latex] ← Equation #1 | [latex]m[/latex] is an integer |
| [latex]b|c[/latex] | [latex]c = bn[/latex] ← Equation #2 | [latex]n[/latex] is an integer |
What should we do next? Well, we can substitute the expression for [latex]b[/latex] of Equation #1 into the [latex]b[/latex] of Equation #2.

After substitution, we get the one below.
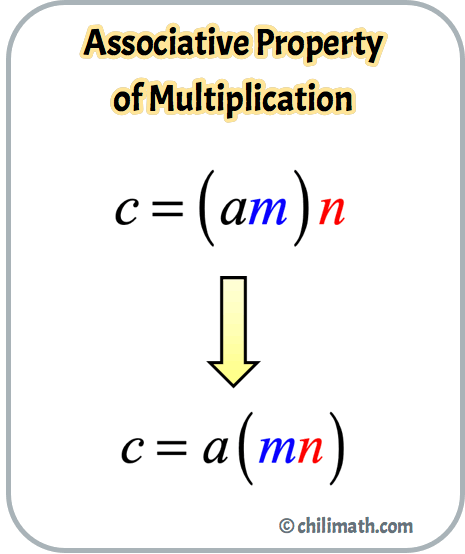
[latex]c = \left( {am} \right)n[/latex]
Apply the Associative Property of Multiplication. Notice that the grouping symbol (parenthesis) moves from [latex]am[/latex] to [latex]mn[/latex].
The Associative Property of Multiplication guarantees that when multiplying numbers, the product is always the same no matter how we group the numbers. Thus, [latex]\left( {am} \right)n = a\left( {mn} \right)[/latex].
This property allows us to rewrite the equation without breaking any math laws because the two equations may look different but they are essentially the same or equivalent.
I hope you can see now why we have to perform such slight adjustment using the Associative Property.
[latex]c = \left( {am} \right)n[/latex] → [latex]c = a\left( {mn} \right)[/latex]
After we substitute the expression of [latex]\large{b}[/latex] from Equation #1 into the [latex]\large{b}[/latex] of Equation #2, and apply the Associative Property of Multiplication, we are ready to move to the next step.
Notice that inside the parenthesis are two arbitrary integers that are being multiplied.
If you remember, there is a simple yet very useful property of the Set of Integers ( the symbol for the set of integers is [latex]\mathbb{Z}[/latex] ).
The property is called the Closure Property of Multiplication. It states that if [latex]m[/latex] and [latex]n[/latex] are integers then the product of [latex]m[/latex] and [latex]n[/latex] is also an integer. Therefore, [latex]m \times n \in[/latex] [latex]\mathbb{Z}[/latex].
From where we left off, we have
[latex]c = a\left( {mn} \right)[/latex].
Since [latex]mn[/latex] is just another integer using the Closure Property of Multiplication, that means we can let [latex]mn = k[/latex] where [latex]k[/latex] is an integer.
We can rewrite [latex]c = a\left( {mn} \right)[/latex] as [latex]c = a\left( {k} \right)[/latex].
The equation [latex]c = a\left( {k} \right)[/latex] can be expressed in notation form as [latex]a|c[/latex] which means that [latex]a[/latex] divides [latex]c[/latex].
This is exactly where we want to show! Now it’s time to write the actual proof.
WRITE THE PROOF
THEOREM: Let [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] be integers with [latex]a \ne 0[/latex] and [latex]b \ne 0[/latex]. If [latex]a|b[/latex] and [latex]b|c[/latex], then [latex]a|c[/latex].
PROOF: Suppose [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are integers where both [latex]a[/latex] and [latex]b[/latex] do not equal to zero. Since [latex]a[/latex] divides [latex]b[/latex], [latex]a|b[/latex], then there exists an integer [latex]m[/latex] such that [latex]b = am[/latex] (Equation #1). Similarly, since [latex]b[/latex] divides [latex]c[/latex], [latex]b|c[/latex], there exists an integer [latex]n[/latex] such that [latex]c=bn[/latex] (Equation #2). Now, substitute the expression of [latex]b[/latex] from Equation #1 into the [latex]b[/latex] in Equation #2. By doing so, the equation [latex]c=bm[/latex] is transformed to [latex]c=(am)n[/latex]. Next, apply the Associative Property of Multiplication on the equation [latex]c=(am)n[/latex] to get [latex]c=a(mn)[/latex]. Because [latex]m[/latex] and [latex]n[/latex] are integers, their product must also be an integer by the Closure Property of Multiplication; that is, [latex]m \times n \in \mathbb{Z}[/latex]. Let [latex]k = m \times n[/latex]. In the equation [latex]c=a(mn)[/latex], substitute [latex]mn[/latex] by [latex]k[/latex] to obtain [latex]c=ak[/latex]. The equation [latex]c=ak[/latex] implies that [latex]a[/latex] divides [latex]c[/latex] or when written in shorthand we have [latex]a|c[/latex]. Therefore, we have proved that [latex]a[/latex] divides [latex]c[/latex]. ◾️
