Length Word Problems

Example 1: A 57-foot wood is cut into two pieces. One piece is 3 feet less than twice the length of the other. What is the length of the longer piece of wood?

Just like in any other kind of word problem, the first step that we have to do is to identify what important pieces of information are given to us in the problem.

In this example, we are told how long the wood is (57 feet) as well as the measurement for one of the two pieces. The given piece is defined using the other piece so let’s call it the second piece and assign the variable [latex]\large{x}[/latex] to represent the first piece. Note that the measurement of the first piece is currently unknown.

Since the second piece is 3 feet less than twice the length of the first piece, then it can be algebraically expressed as [latex]2{\large{x}} – 3[/latex].

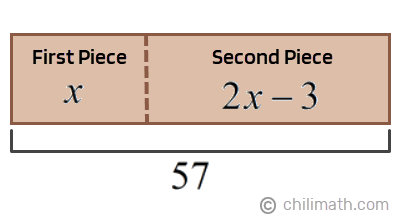
So we have,

• Total Length: [latex]57[/latex]
• First Piece: [latex]\large{x}[/latex]
• Second Piece: [latex]2{\large{x}}-3[/latex]

Now that we have all this information, let’s go ahead and solve for [latex]\large{x}[/latex] so we can find the measurements for both pieces.

Luckily for length word problems, we don’t have to remember any particular formula. We simply have to set up our equation where we add all the pieces on one side and the total length of the object on the other.

First Piece + Second Piece = Total Length

Let’s solve for [latex]\large{x}[/latex].

Going back to our original problem, it asks us for the measurement of the longer piece. At this point, we only know that the first piece is 20 feet long. In order to determine which one is longer, we’ll use the value of [latex]\large{x}[/latex] to also find the length of the second piece. Therefore,

• First Piece = [latex]20[/latex]
• Second Piece = [latex]2x-3[/latex] = [latex]2({\color{red}20}) – 3[/latex] = [latex]40-3[/latex] = [latex]37[/latex]

Answer: The longer piece of wood is 37 feet long.

Check:

Before we move on to the next problem, let’s do a quick check to make sure that we got the correct answers. We were told that the total length of the wood is 57 feet. So we’ll check if the measurements of our pieces indeed sum up to 57.

First Piece + Second Piece = Total Length

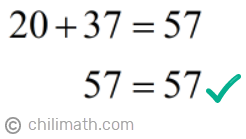
And it did! With this quick check, we were able to verify that the measurements we got for both pieces are correct.

---

Example 2: A wire is cut into two pieces. The shorter piece is 1 meter more than half the longer piece. The length of the wire is 28 meters. What is the measure of the shorter piece?

This next example is quite similar to the first one. Right away, we can see that the shorter wire is defined using the length of the longer wire. The length of the longer wire at this point is unknown, so let’s use the variable [latex]L[/latex] to represent it.

So what do we have?

• Total Length: [latex]28[/latex]
• Longer Piece: [latex]L[/latex]
• Shorter Piece: 1 meter more than half the longer piece → [latex]{\Large{{L \over 2}}} + 1[/latex]

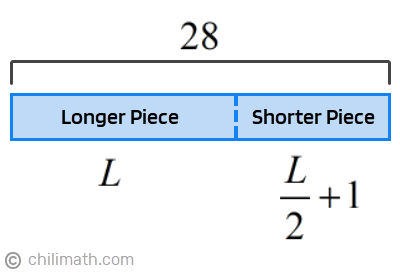
Let’s now proceed to solve for [latex]L[/latex] by adding the longer piece and the shorter piece then set it equal to the total length of the wire. So we have,

Longer Piece + Shorter Piece = Total Length

Great! We now know that our longer piece is 18 feet long. But since the problem is asking for the measurement of the shorter piece, we’ll use the value of [latex]L[/latex] which is [latex]18[/latex], to also find out how long the shorter piece is.

• Longer Piece: [latex]18[/latex]
• Shorter Piece: [latex]{\Large{{L \over 2}}} + 1[/latex] = [latex]{\Large{{{\color{red}18} \over 2}}} + 1[/latex] = [latex]9+1[/latex] = [latex]10[/latex]

Answer: The length of the shorter piece of wire is 10 meters.

Check:

To verify, let’s add both of the pieces to see if they equal the total length of the wire which is 28 meters.

Longer Piece + Shorter Piece = Total Length

---

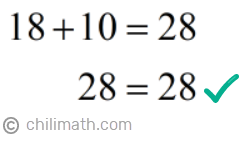
Example 3: A piece of board is cut into three segments. The second segment is 3 inches more than the first segment. The third segment is twice as long as the second segment. If the board is 117 inches, what is the length of the third segment?

Here we have an object that is divided into three. As you can see, the 2nd segment is described in terms of the measurement of the 1st segment while the 3rd segment is defined using the length of the 2nd segment. How about the 1st segment? Well, this segment is unknown right now so let’s represent it with the variable [latex]F[/latex].

Looking back at our word problem, here are the information that we have so far.

• Total Length: 117
• First Segment: [latex]F[/latex]
• Second Segment: 3 inches more than the 1st segment → [latex]F+3[/latex]
• Third Segment: twice as long as the 2nd segment → [latex]2(F+3)[/latex]

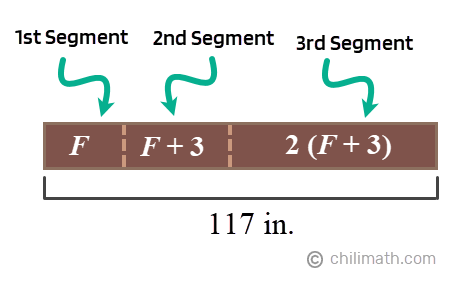
We’ll proceed by setting up our equation and solving for [latex]F[/latex].

1st Segment + 2nd Segment + 3rd Segment = Total Length

As you know, we used the variable [latex]F[/latex] to represent the 1st segment of the board. Therefore, we can say that the 1st segment is 27 in. long. Since our problem is asking us to find how long the 3rd segment is (which is currently defined using the 2nd segment), this means that we also have to find the measurements of both the 2nd and 3rd segments.

• 1st Segment: [latex]27[/latex]
• 2nd Segment: [latex]F+3[/latex] = [latex]{\color{red}27}+3[/latex] = [latex]30[/latex]
• 3rd Segment: [latex]2(F+3)[/latex] = [latex]2({\color{red}30})[/latex] = [latex]60[/latex]

Answer: The length of the third segment is 60 inches.

Check:

Let’s do a quick check if all the segments, when added, will give us the total length of the board which is 117 inches.

1st Segment + 2nd Segment + 3rd Segment = Total Length

---

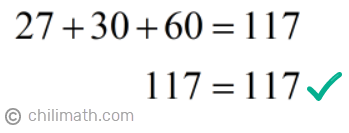
Example 4: A stick is broken into three pieces. The second piece is twice the length of the first piece. The third piece is the average of the first piece and the second piece. The length of the stick is 207 centimeters. Which among the pieces has a measurement that is between the shortest and the longest piece and what is its dimension?

This problem is quite interesting and I must say, is packed with a lot of information. However, do not let that overwhelm you. As long as you continue to follow the steps that we’ve been doing in our previous examples, you’ll realize that this problem isn’t as hard as it looks.

What details are given to us?

• Total Length: [latex]207[/latex]
• 1st Piece: [latex]\large{x}[/latex]
• 2nd Piece: twice the length of the first piece → [latex]2{\large{x}}[/latex]
• 3rd Piece: the average of the first piece and the second piece → [latex]\Large{{{x + 2x} \over 2}}[/latex]

As you can see, we used the variable [latex]\large{x}[/latex] to stand for the first piece which is currently unknown, because it is not defined using the second piece nor the third piece.

Our next step is to solve for [latex]\large{x}[/latex].

Using the value of [latex]\large{x}[/latex], let’s find out how long each piece of the broken stick is.

• 1st Piece: [latex]46[/latex]
• 2nd Piece: [latex]2x[/latex] → [latex] 2({\color{red}46})[/latex] → [latex]92[/latex]
• 3rd Piece: [latex]\Large{{{x + 2x} \over 2}}[/latex] → [latex]\Large{{{{\color{red}46} + {\color{red}92}} \over 2}}[/latex] → [latex]\Large{{{138} \over 2}}[/latex] → [latex]69[/latex]

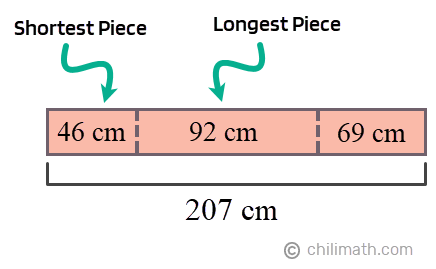
Going back to our original question…which among the pieces has a measurement that is between the shortest and the longest piece, and what is its dimension?

Answer: The third piece of the stick which is 69 centimeters long has the measurement that is between the shortest and the longest pieces.

This time, I’ll leave it up to you to check if the measurements that we got for the three pieces indeed sum up to 207 cm.

---

Example 5: A rope is cut into two pieces. If the first piece is added to the second piece, the sum is 25 yards. In addition, twice the first piece plus the second piece equals 40 yards. What is the measure of the shorter piece?

Now this problem is a little tricky. If you notice, none of the two pieces are described in terms of the other.

To start, let us identify the pieces of information that are given in the problem and translate each statement algebraically into an equation.

Let’s use the variables [latex]F[/latex] and [latex]S[/latex] to represent the first piece and second piece, respectively.

1) If the first piece is added to the second piece, the sum is 25 yards.

[latex]F + S = 25[/latex]

2) Twice the first piece plus the second piece equals 40 yards.

[latex]2F + S = 40[/latex]

Going through both statements, we are able to come up with two equations.

• Equation 1: [latex]F + S = 25[/latex]
• Equation 2: [latex]2F + S = 40[/latex]

As you can see, we are dealing with two equations with two unknowns, [latex]F[/latex] and [latex]S[/latex] which means we will be solving systems of linear equations with two variables.

Our next step is to use Equation 1 to express the second piece ([latex]S[/latex]) in terms of the first piece ([latex]F[/latex]). Then we can substitute the expression that we get into Equation 2. In doing so, we will have a multi-step equation with only [latex]F[/latex] as the only variable instead of having both.

Note that we can also do the other way around. That is, expressing the first piece in terms of the second piece. However, for this example, we’ll solve for the variable [latex]S[/latex].

We’ll do this step-by-step so it’s easy to understand and follow.

1) Start with Equation 1. Solve for [latex]S[/latex].

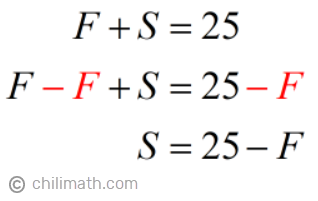
2) Next, substitute the expression of [latex]S[/latex] into Equation 2.

Remember that the variable [latex]F[/latex] stands for the first piece. Therefore, we can now say that the first piece is 15 yards. However, since our problem is asking us for the measure of the shorter piece, we also need to find how long the second piece is, so we can compare and identify between the two (1st piece and 2nd piece) which one is shorter.

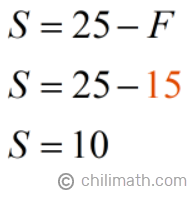
So we have,

• First Piece: [latex]15[/latex] yards
• Second Piece: [latex]10[/latex] yards

We now know that the second piece then is the shorter piece. Let’s go ahead and answer the original question.

Answer: The shorter piece is 10 yards long.

Check:

In order to verify that our answers are correct, we’ll substitute the values of [latex]F[/latex] and [latex]S[/latex] into both Equations 1 and 2. In doing so, we’ll be able to prove that the statements given in the word problem are true.

• Equation 1

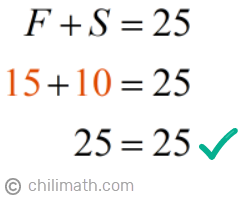
• Equation 2

---

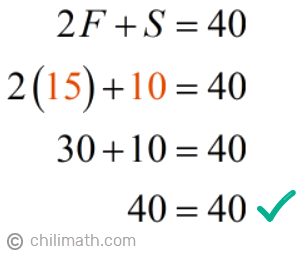
Example 6: A piece of wood is cut into two. The sum of the first piece and the second piece is 71 inches. The difference of 4 times the first piece and twice the second piece is 20 inches. What is the measure of the longer piece?

This one is similar to what we just discussed in Example 5. Since neither of the two pieces is defined in terms of the other piece, let’s look at the important pieces of information that are given to us in the problem.

Like our previous example, we’ll examine each of the statements first then translate them algebraically.

Let [latex]\large{x}[/latex] be the first piece and [latex]\large{y}[/latex] be the second piece.

1) The sum of the first piece and the second piece is 71 inches.

Equation 1: [latex]\large{x + y = 71}[/latex]

2) The difference of 4 times the first piece and twice the second piece is 20 inches.

Equation 2: [latex]\large{4x – 2y = 20}[/latex]

Now that we have our two equations, let’s express the first piece ([latex]\large{x}[/latex]) in terms of the second piece ([latex]\large{y}[/latex]).

• Using Equation 1, let’s solve for [latex]\large{x}[/latex]. So we have,

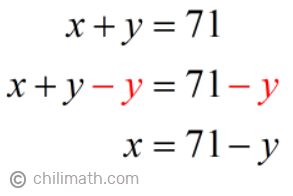
• Substitute the expression of [latex]\large{x}[/latex] into Equation 2.

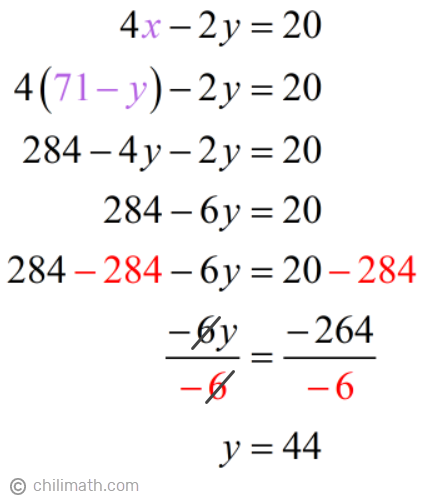
Looking back at our original problem, it’s asking us for the measure of the longer piece. At this point, we know that the second piece ([latex]\large{y}[/latex]) is 44 in. long. But is it the longer piece? Well, we don’t know yet. We have to know how long the first piece ([latex]\large{x}[/latex]) as well so we can determine which one is longer.

We already have our expression for [latex]\large{x}[/latex], so all we need to do is substitute the value of [latex]\large{y}[/latex] into the expression.

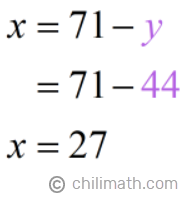
Okay, let’s do a recap. The measurements for our two pieces are:

• First Piece: [latex]27[/latex] in.
• Second Piece: [latex]44[/latex] in.

Perfect! Now we know that the second piece is longer than the first piece.

Going back to the original question, what is the measure of the longer piece?

Answer: The longer piece is 44 inches long.