Logarithms Explained
If you are familiar with the exponential function [latex]{b^N} = M[/latex] then you should know that its logarithmic equivalence is [latex]{\log _b}M = N[/latex]. These two seemingly different equations are in fact the same or equivalent in every way. Look at their relationship using the definition below.
Definition of a Logarithmic Function
Let [latex]b[/latex] a positive number but [latex]b \ne 1[/latex]. We say [latex]{\log _b}M = N[/latex] (read
[latex]\Large{{\log _b}M = N \leftrightarrow {b^N} = M}[/latex]
The purpose of the equivalent equations, as shown above, is to provide a direct link between logarithmic form and exponential form. Understanding this basic concept can help us solve some algebra problems that require switching from one form to another.
Let’s examine further how the variables M, N, and b are rearranged when the logarithmic form is expressed as exponential form and vice versa.
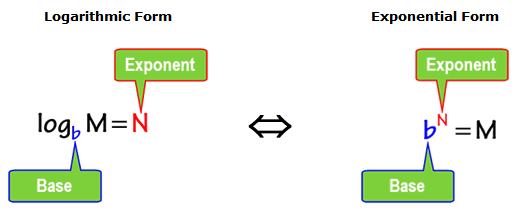
Observations of the “switch” in positions of the variables:
- The subscript b in log form becomes the base in exponential form.
- The base N in log form becomes the exponent or superscript of b in exponential form.
- The variable M is isolated on one side of the equation.
Here are a few quick illustrations on how to convert from the logarithmic form to the exponential form, and vice versa.
Logarithmic Form ⟷ Exponential Form
[latex]{\log _3}81 = 4 \,\,\leftrightarrow\,\, {3^4} = 81[/latex]
[latex]{\log _2}32 = 5 \,\,\leftrightarrow\,\, {2^5} = 32[/latex]
[latex]{\log _5}125 = 3 \,\,\leftrightarrow\,\, {5^3} = 125[/latex]
[latex]{\log _7}49 = 2 \,\,\leftrightarrow\,\, {7^2} = 49[/latex]
[latex]{\log _8}512 = 3 \,\,\leftrightarrow\,\, {8^3} = 512[/latex]
[latex]{\log _{10}}100 = 2 \,\,\leftrightarrow\,\, {10^2} = 100[/latex]
[latex]{\log _{10}}1,000 = 3 \,\,\leftrightarrow\,\, {10^3} = 1,000[/latex]
[latex]{\log _{10}}10,000 = 4 \,\,\leftrightarrow\,\, {10^4} = 10,000[/latex]
[latex]{\log _{64}}2 = {1 \over 6} \,\,\leftrightarrow\,\, {64^{{1 \over 6}}} = 2[/latex]
[latex]{\log _{81}}3 = {1 \over 4} \,\,\leftrightarrow\,\, {81^{{1 \over 4}}} = 3[/latex]
Now we are going to discuss “special cases” that naturally arise from the basic definition of logarithm in terms of exponential equation. We will use the definition above in order to answer some of these questions. The best way to point out the concept is through the use of examples.
Examples of How to Solve Basic Logarithmic Equations
Example 1: Solve for y in logarithmic equation log33 = y.
Rewriting the logarithmic equation log33 = y into exponential form we get 3 = 3y. What do you think is the value of y that can make the exponential equation true? In other words, we want to find the exponent in which 3 be raised in order to get 3. It looks like the only answer is 1 because when [latex]y = 1[/latex] we have 3=31.
In fact, we can generalize this idea into a simple rule…
The logarithm of a nonzero and nonnegative number wherein the base is the number itself is ALWAYS equal to 1.
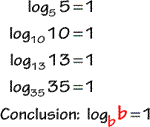
Example 2: Solve for x in logarithmic equation log81 = x.
This logarithmic equation in exponential form is written as 1 = 8x. What could possibly be the value of the exponent x in order to make it a true statement? Using the Zero Property of exponent, b0 = 1, we know that any number (exception of zero), when raised to zero, is always equal to 1. It makes perfect sense that in 1 = 8x, the value must be x = 0 because 80= 1 .
There’s also a rule that handles such cases when we attempt to get the logarithm of 1 with any base.
The logarithm of 1 with any value of b ( b is a positive number but b ≠1) is ALWAYS equal to zero (0).
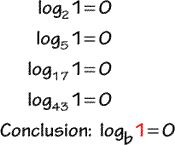
Example 3: Solve for [latex]k[/latex] in logarithmic equation log4(−1) = k.
Transforming into an exponential equation, we have −1 = 4k. This is like a “trick” question, right? We need to find the exponent k to make the exponential equation a true statement.
Is there really such value? I don’t think there is one! In fact, we can’t find any number that we can raise 4 by to give −1. Therefore we say that there’s no solution, or undefined.
The logarithm of a negative number is undefined.

Example 4: Solve for w in logarithmic equation log2(0) = w.
The last “special case” happens when we try to find the logarithm of zero. Converting that log equation again into exponential we obtain 0 = 2w. We are faced again with an odd situation because we want to raise the base 2 by some exponent so that it results in zero. Is there such value? You can try. But you should agree that no such value exists! Therefore, this is another case where our answer is undefined or no solution.
The logarithm of zero is undefined.

You may also be interested in these related math lessons or tutorials:
