How to Compose Functions
In this lesson, I will go over eight (8) worked examples to illustrate the process involved in function composition.
If we are given two functions, it is possible to create or generate a “new” function by composing one into the other. The step involved is similar when a function is being evaluated for a given value. For instance, evaluate the function below for [latex]x = 3[/latex].
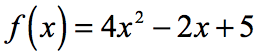
It is obvious that I need to replace each [latex]x[/latex] with the given value and then simplify.
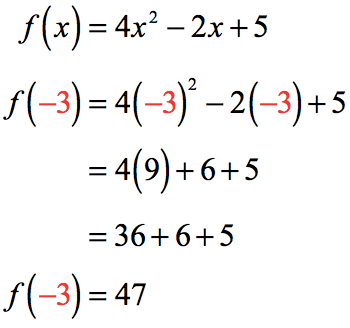
The key idea in function composition is that the input of the function is not a numerical value, instead, the input is also another function.
General Rule of Composition of Function
Suppose the two given functions are [latex]f[/latex] and [latex]g[/latex], the composition of [latex]f \circ g[/latex] is defined by

Also, the composition of [latex]g \circ f[/latex] is defined by
Few notes about the symbolic “formula” above:
- The order in function composition matters! You always compose functions from right to left. Therefore, given a function, its input is always the one to its right side. In other words, the right function goes inside the left function.
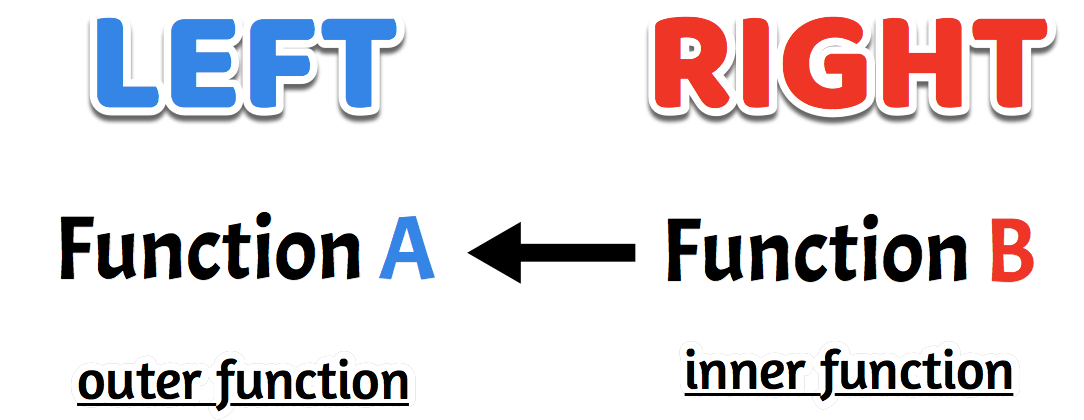
- Notice in [latex]f \circ g = f\left[ {g\left( x \right)} \right][/latex] , the input or “inner function” is function [latex]g[/latex] because it is to the right of function [latex]f[/latex]which is the main or “outer function”.
- In terms of the order of composition, do you see the same pattern in [latex]g \circ f = g\left[ {f\left( x \right)} \right][/latex] ? That’s right! The function [latex]f[/latex] is the inner function of the outer function [latex]g[/latex].
Let us go over a few examples to see how function composition works. You will realize later that it is simply an exercise of algebraic substitution and simplification.
Examples of How to Compose Functions
Example 1: Perform the indicated function composition:
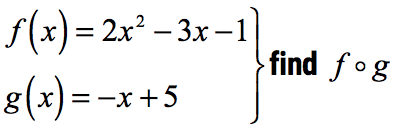
The order of composition is important. Notice that in [latex]f \circ g[/latex] , we want the function [latex]g\left( x \right)[/latex] to be the input of the main function [latex]{f\left( x \right)}[/latex].
It should look like this:
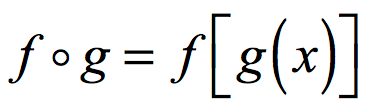
I start by writing down the main or outer function [latex]f\left( x \right)[/latex] , and in every instance of [latex]x[/latex], I will substitute the full value of [latex]g\left( x \right)[/latex].
Then, I’ll do whatever is needed to simplify the expressions such as squaring the binomial, applying the distributive property, and combining like terms. Other than that, there’s really nothing much to it.
Let me show you what I meant by that.

Example 2: Perform the indicated function composition:
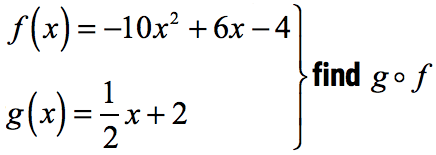
I need to find the composite function [latex]g \circ f[/latex] which means function [latex]f[/latex] is the input of function [latex]g[/latex].

Example 3: Perform the indicated function composition:
This is an example of function composition where the input is a square root function. Let’s see how it works out.
Again, in [latex]f \circ g[/latex] we want to plug in function [latex]g[/latex] into the function [latex]f[/latex].

Example 4: Perform the indicated function composition:
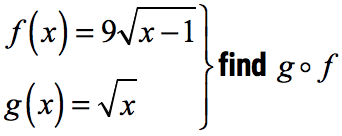
This composition of
The key to correctly composing this function is to recognize that the square root symbol can be expressed as an exponential expression with a fractional exponent equaling to [latex]{1 \over 2}[/latex].
Thus, we have [latex]\sqrt {x – 1} = {\left( {x – 1} \right)^{{1 \over 2}}}[/latex] and [latex]\sqrt x = {\left( x \right)^{{1 \over 2}}}[/latex].

Example 5: Perform the indicated function composition:
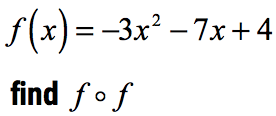
So far in our previous examples, we have performed function compositions using two distinct functions. However, it is also possible to compose a function with itself.
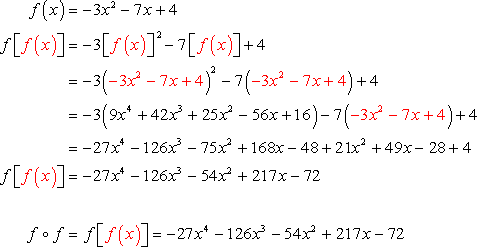
Example 6: Perform the indicated function composition:
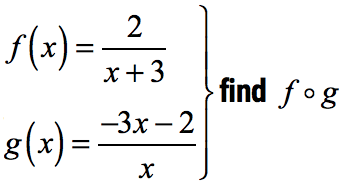
Let us work out an example of a function composition that deals with rational functions. The algebra involved is a bit tedious, however, you should be okay as long as you are careful in simplifying the expressions in every step of the way.
In this example, you will apply the procedures on how to add or subtract rational expressions, and also on how to multiply rational expressions.
Here we go…
![This seemingly complicated composition of function problem when reduced has a very simple answer. The steps are as follows: write down the outer function, substitute the input function, add the complex denominator using LCD method, combine like terms on the numerator , divide by multiplying the numerator to the reciprocal of the denominator, then finally simplify the expression by canceling common factors. So we have, f=2/ =2/ = 2 / = 2/ = 2 * [x/(-2)]= -x. The final solution is f o g = f = -x.](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_sol.gif)
That wasn’t too bad, right?
Example 7: Perform the indicated function composition:
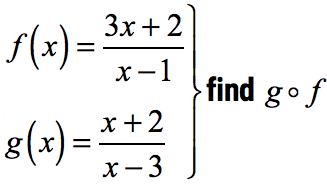
If you think that our last example of rational function composition was messy, wait till you see this next example. It can be a bit messier but still very manageable. So don’t fret! Always have that “laser” focus in every simplification process in order to successfully work this out correctly.
The input function [latex]f[/latex] will be substituted into every [latex]x[/latex] of the main function [latex]g[/latex].
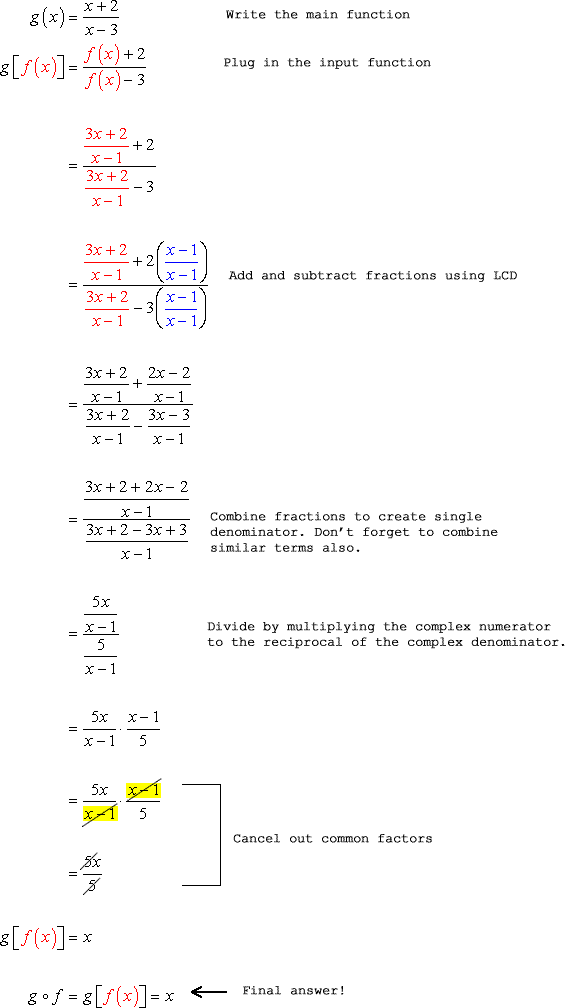
That was easy, wasn’t it?
For more practice, I suggest that you try reversing the order of function composition. In other words, find [latex]f \circ g[/latex] .
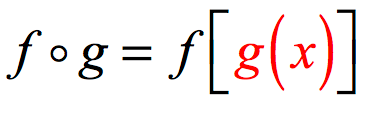
Do you also get?
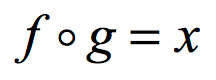
If that’s the case where [latex]g \circ f = f \circ g = x[/latex], then we conclude that functions [latex]g[/latex] and [latex]f[/latex] are inverses of each other. I have a separate tutorial on how to prove or verify if two functions are inverse of each other.
Example 8: Find the composite function:
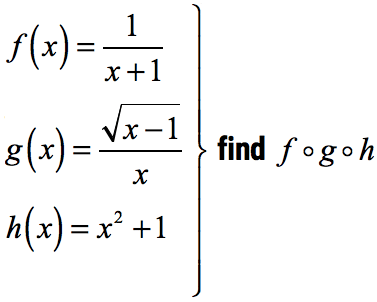
In this example, we are going to compose three functions. Observing the notation of the desired composite function [latex]f \circ g \circ h[/latex], we are going to work it out from right to left.
I first need to plug in function [latex]h[/latex] into function [latex]g[/latex] then simplify to get a new function.
The output of the previous step will be substituted further into the main function [latex]f[/latex] to obtain the final answer. Symbolically, it looks like this…
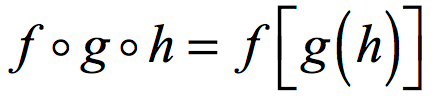
Here we go…
I will start by finding the composition [latex]g \circ h = g\left( h \right)[/latex] .
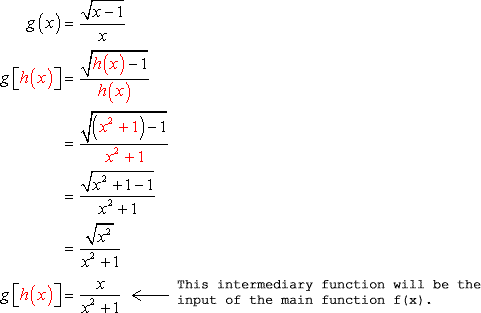
The result of [latex]g\left( h \right) = {\Large{{x \over {{x^2} + 1}}}}[/latex] becomes the input of function [latex]f[/latex]
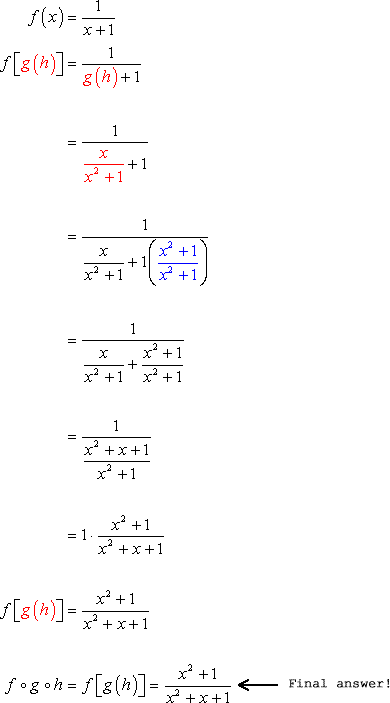
You may also be interested in these related math lessons or tutorials:
