How to Find the X-Intercepts and Y-Intercepts
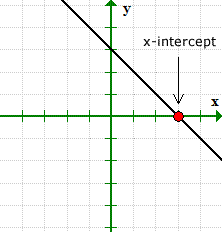
The X-Intercepts
The x-intercepts are points where the graph of a function or an equation crosses or “touches” the [latex]x[/latex]-axis of the Cartesian Plane. You may think of this as a point with [latex]y[/latex]-value of zero.
- To find the [latex]x[/latex]-intercepts of an equation, let [latex]y = 0[/latex] then solve for [latex]x[/latex].
- In a point notation, it is written as [latex]\left( {x,0} \right)[/latex].
x-intercept of a Linear Function or a Straight Line
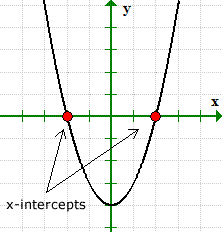
x-intercepts of a Quadratic Function or Parabola
The Y-Intercepts
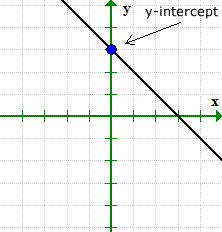
The y-intercepts are points where the graph of a function or an equation crosses or “touches” the [latex]y[/latex]-axis of the Cartesian Plane. You may think of this as a point with [latex]x[/latex]-value of zero.
- To find the [latex]y[/latex]-intercepts of an equation, let [latex]x = 0[/latex] then solve for [latex]y[/latex].
- In a point notation, it is written as [latex]\left( {0,y} \right)[/latex].
y-intercept of a Linear Function or a Straight Line
y-intercept of a Quadratic Function or Parabola
Examples of How to Find the x and y-intercepts of a Line, Parabola, and Circle
Example 1: From the graph, describe the [latex]x[/latex] and [latex]y[/latex]-intercepts using point notation.
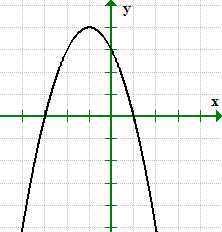
The graph crosses the [latex]x[/latex]-axis at [latex]x= 1[/latex] and [latex]x= 3[/latex], therefore, we can write the [latex]x[/latex]-intercepts as points [latex](1,0)[/latex] and [latex](–3, 0)[/latex].
Similarly, the graph crosses the [latex]y[/latex]-axis at [latex]y=3[/latex]. Its y-intercept can be written as the point [latex](0,3)[/latex].
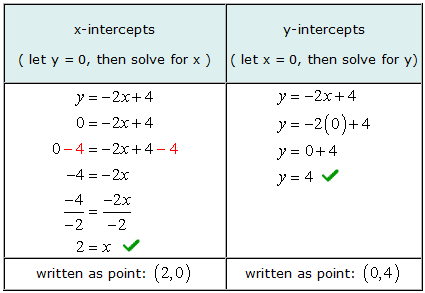
Example 2: Find the x and y-intercepts of the line [latex]y = – 2x + 4[/latex].
To find the x-intercepts algebraically, we let [latex]y=0[/latex] in the equation and then solve for values of [latex]x[/latex]. In the same manner, to find for [latex]y[/latex]-intercepts algebraically, we let [latex]x=0[/latex] in the equation and then solve for [latex]y[/latex].
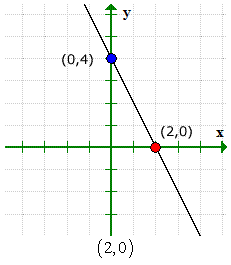
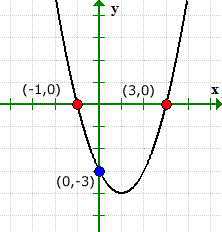
Here’s the graph to verify that our answers are correct.
Example 3: Find the [latex]x[/latex] and [latex]y[/latex]-intercepts of the quadratic equation [latex]y = {x^2} – 2x – 3[/latex].
The graph of this quadratic equation is a parabola. We expect it to have a “U” shape where it would either open up or down.
To solve for the [latex]x[/latex]-intercept of this problem, you will factor a simple trinomial. Then you set each binomial factor equal to zero and solve for [latex]x[/latex].
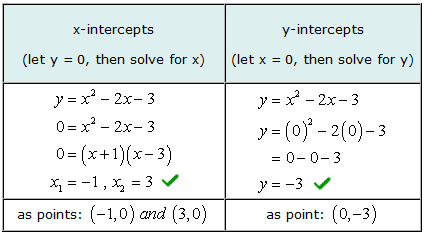
Our solved values for both [latex]x[/latex] and [latex]y[/latex]-intercepts match with the graphical solution.
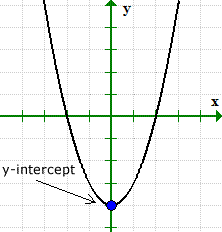
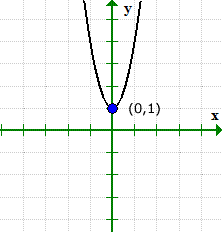
Example 4: Find the [latex]x[/latex] and [latex]y[/latex]-intercepts of the quadratic equation [latex]y = 3{x^2} + 1[/latex].
This is an example where the graph of the equation has a y-intercept but without an [latex]x[/latex]-intercept.
- Let’s find the [latex]y[/latex]-intercept first because it’s extremely easy! Plug in [latex]x = 0[/latex] then solve for [latex]y[/latex].
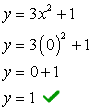
- Now for the [latex]x[/latex]-intercept. Plug in [latex]y = 0[/latex], and solve for [latex]x[/latex].
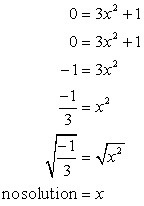
The square root of a negative number is imaginary. This suggests that this equation does not have an [latex]x[/latex]-intercept!
The graph can verify what’s going on. Notice that the graph crossed the [latex]y[/latex]-axis at [latex](0,1)[/latex], but never did with the [latex]x[/latex]-axis.
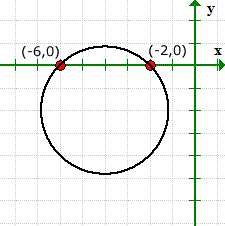
Example 5: Find the x and y intercepts of the circle [latex]{\left( {x + 4} \right)^2} + {\left( {y + 2} \right)^2} = 8[/latex].
This is a good example to illustrate that it is possible for the graph of an equation to have [latex]x[/latex]-intercepts but without [latex]y[/latex]-intercepts.
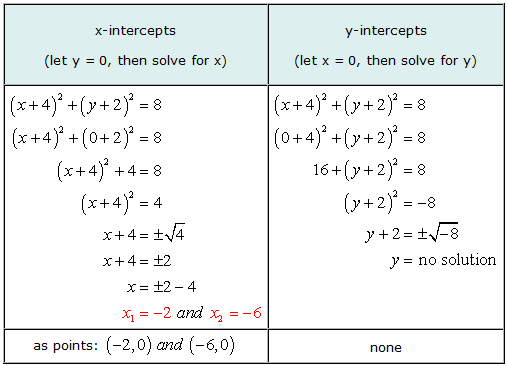
When solving for [latex]y[/latex], we arrived at the situation of trying to get the square root of a negative number. The answer is imaginary, thus, no solution. That means the equation doesn’t have any [latex]y[/latex]-intercepts.
The graph verifies that we are right for the values of our [latex]x[/latex]-intercepts, and it has no [latex]y[/latex]-intercepts.