Finding the Greatest Common Factor using the List Method
The greatest common factor, also known as GCF, of two numbers is the largest number that can evenly divide the given two numbers.
Another way to define GCF: The greatest common factor of two numbers is the largest factor that is common to both numbers.
The two definitions above mean the same thing.
Don’t be confused if you encounter other names of the greatest common factor. They all have the same meaning. The alternate names of GCF are:
- Greatest Common Divisor which is abbreviated as GCD
- Highest Common Factor which is abbreviated as HCF

Before you continue, make sure that you know how to find all the factors of a number. Otherwise, please review my short lesson on how to find all factors of a number using the rainbow method.
Steps on How to Find the Greatest Common Factor
Step 1: List or write ALL the factors of each number.
Step 2: Identify the common factors. You can do that by encircling each common factor or drawing a line segment between them. It’s really up to you how you want to mark the common factors so they stand out.
Step 3: After identifying the common factors, select or choose the number which has the largest value. This number will essentially be the Greatest Common Factor (GCF).
Examples of How to Find the Greatest Common Factors
NOTE: I decided to focus on finding the GCF of two numbers because they are the most common problems that you will encounter when studying GCF.
Example 1: Find the Greatest Common Factor of [latex]12[/latex] and [latex]18[/latex].
This problem is easy because the numbers involved are relatively simple. You should be able to find all the factors of 12 and 18 using the rainbow method. As an alternative, I have listed all the factors of numbers from 1 to 100 for you to use at your own convenience.
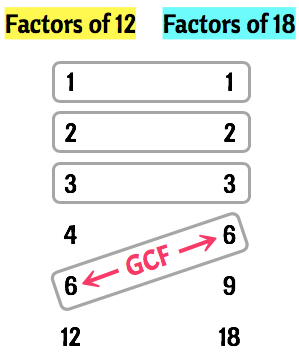
So here are all the factors of both [latex]12[/latex] and [latex]18[/latex].
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18

After listing all the factors of each number, we now identify the common factors. As you can see below, the common factors of [latex]12[/latex] and [latex]18[/latex] are [latex]1[/latex], [latex]2[/latex], [latex]3[/latex], and [latex]6[/latex]. Notice that I identified the common factors by enclosing them in a “rectangle”.

So what is the GCF then? Obviously, the GCF is one of the common factors. The common factor which has the largest value is actually the Greatest Common Factor. Therefore the GCF of [latex]12[/latex] and [latex]18[/latex] is [latex]6[/latex]. That’s it!
Example 2: Find the Greatest Common Factor of [latex]64[/latex] and [latex]96[/latex].
In many instances in math, as the number becomes larger, the level of difficulty of the problem also increases. Yes, this is true as well when finding the GCF of two large numbers. However, the concept or procedure never changes.
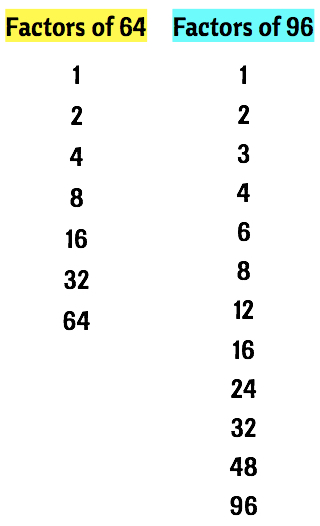
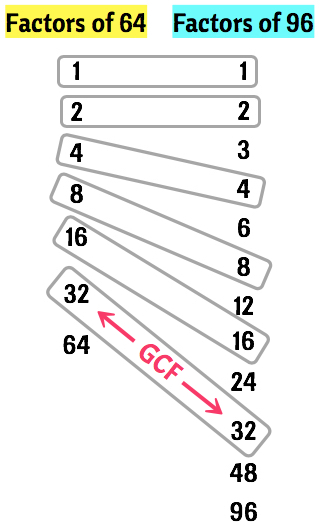
So here we go. Let’s find the complete factors of [latex]64[/latex] and [latex]96[/latex].
◉ The complete factors of [latex]64[/latex] are 1, 2, 4, 8, 16, 32, and 64.
◉ While the complete factors of [latex]96[/latex] are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.
Below are the lists of factors in a vertical format.
The next step is to compare the lists of factors. Then draw a shape so that the common factor is inside each shape. You can be creative here! Notice that on the illustration below, we have six (6) common factors which are [latex]1[/latex], [latex]2[/latex], [latex]4[/latex], [latex]8[/latex], [latex]16[/latex], and [latex]32[/latex].
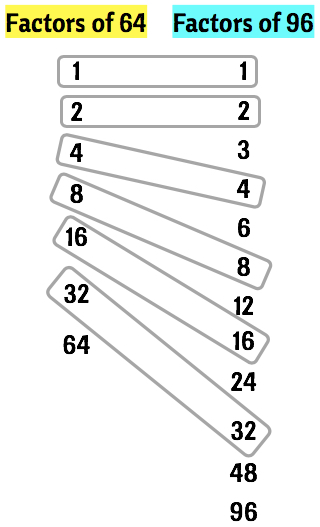
By looking at the common factors, the one which has the biggest value is [latex]32[/latex]. Therefore, the greatest common factor of [latex]64[/latex] and [latex]96[/latex] is simply [latex]32[/latex].
Example 3: Determine the Greatest Common Factor of [latex]42[/latex] and [latex]126[/latex].
It is easy to rush into solving a math problem because you are already familiar with the steps on how to work it out. However, it is a good practice to pause or step back and look at the problem from a broader perspective before delving into the process of solving the problem itself.
The reason is, that the procedure that you already know may not be the most time-efficient because there might be a better way, that is, a shorter solution.
Let’s approach it this way. If [latex]42[/latex] can divide [latex]126[/latex] without a remainder, then it implies that [latex]42[/latex] is a factor of [latex]126[/latex]. Not only that [latex]42[/latex] is a common factor of [latex]42[/latex] and [latex]126[/latex], but it is also the common factor that has the highest value.
If you think about it, it is not possible to have a common factor greater than [latex]42[/latex] because it cannot be more than the smaller number of the given two numbers.
So, does [latex]42[/latex] divide [latex]126[/latex] evenly? The answer is yes! Therefore, the greatest common divisor (GCD) of [latex]42[/latex] and [latex]126[/latex] is simply [latex]42[/latex]. Done!
Example 4: What is the GCF of [latex]71[/latex] and [latex]223[/latex] ?
Just like with example #3, don’t jump into the motion of applying the steps that you already know. I can’t overemphasize the importance of practicing restraint when solving math problems in general. Stepping back to see the big picture is extremely important because this will allow you to strategize and therefore be able to devise a viable approach to the problem.
So now, if you closely examine the two numbers which are [latex]71[/latex] and [latex]223[/latex], you should easily recognize that both of them are prime numbers. Remember that a prime number has exactly two factors which are [latex]1[/latex] and itself. In other words, we can say that a prime number is only divisible by [latex]1[/latex] and itself.
Listing the factors of [latex]71[/latex] and [latex]223[/latex]:
Factors of 71: 1, 71
Factors of 223: 1, 223
We should be able to conclude that since [latex]1[/latex] is the ONLY common factor, it implies that [latex]1[/latex] must also be the greatest common factor by default. Thus, [latex]{\rm{gcf}}\left( {71,223} \right) = 1[/latex].
Example 5: What is the GCF of [latex]72[/latex] and [latex]84[/latex] ?
First, we know that both numbers are not prime, in fact, both are even numbers. It means they have common factors other than [latex]1[/latex]. Secondly, it is obvious too that the smaller number [latex]72[/latex] cannot evenly divide the larger number [latex]84[/latex]. This leaves us to conclude that the smaller of the two numbers, [latex]72[/latex], is NOT the greatest common factor either.
Well, the only option left is to proceed with the step-by-step procedure of finding the GCF of two numbers as discussed in the first part of this lesson.
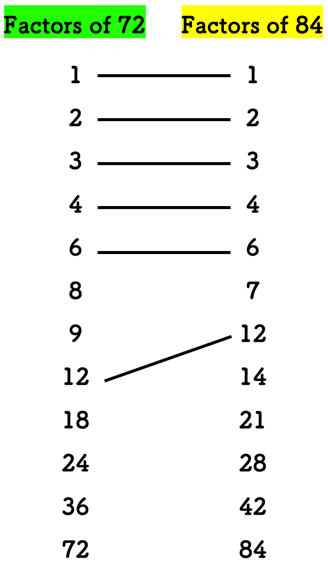
Listing all the factors of each number, we have:
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84

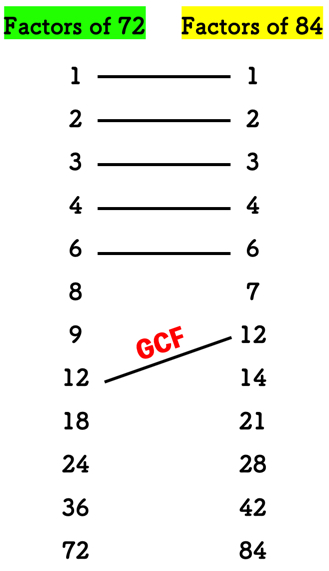
Comparing the lists of factors, the common factors of 72 and 84 are 1, 2, 3, 4, 6, and 12.
Taking it from the diagram, [latex]12[/latex] is the greatest common factor of [latex]72[/latex] and [latex]84[/latex]. Done!
You may also be interested in these related math lessons or tutorials:
Use Prime Factorization to Find GCF
