Factoring Trinomial Easy Case
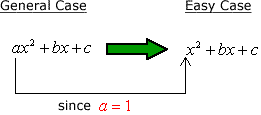
The general form of a quadratic trinomial is written as [latex]a{x^2} + bx + c[/latex] where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are constants. The “easy” case happens when the value of [latex]a[/latex] is equal to [latex]+1[/latex] or [latex] – 1[/latex], that is [latex]a = 1[/latex] or [latex]a = – 1[/latex]. You don’t need to write the coefficient of [latex]1[/latex] before the [latex]{x^2}[/latex] term because it is understood.
If you are up for a challenge, I have another lesson on factoring trinomial where the absolute value of the leading coefficient is not equal to [latex]1[/latex]. It is called Factoring Trinomials (“Hard Case”). Believe me, it is not really that hard. You will just have to perform extra steps.
Thus, the general form of the “easy” case is reduced to
Easy Case of a Trinomial
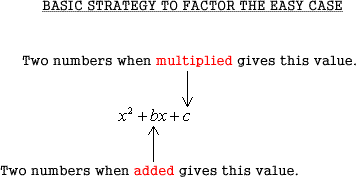
The basic strategy to factor this type of trinomial is to find two numbers (factor pair) which when multiplied, give the constant number [latex]c[/latex]. More so, their sum (when added together) should equal to constant [latex]b[/latex], the coefficient of the [latex]x[/latex] term.
Going over some examples should help you get comfortable with the steps. Let’s begin!
Examples of How to Factor a Trinomial where [latex]a=1[/latex] (Easy Case)
Example 1: Factor the trinomial [latex]x^2+7x+10[/latex] as a product of two binomials.
Obviously, this is an “easy” case because the coefficient of the squared term [latex]x[/latex] is just 1. This is great! We can now focus on the steps to factor this out.
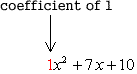
In this trinomial, we need to identify the other relevant constants. Observe that b= 7 and c= 10. Check out the correspondence below.
Next, find two numbers (factor pair) that when multiplied equals the constant value of [latex]c=10[/latex], and when added equals the constant value of [latex]b=7[/latex]. Because the product of two numbers must be positive, the two numbers should be both positive, or both negative.
To find the pair, you can perform several trial and error to find the correct combination. Here are some possible combinations.
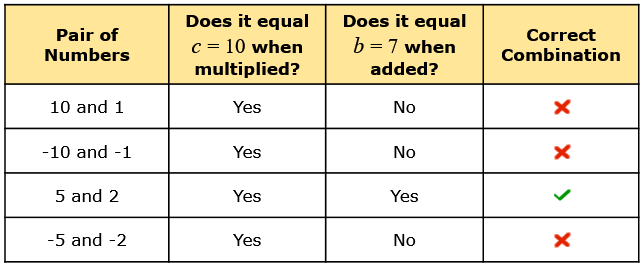
The only combination of numbers that can satisfy the two given requirements is the third option. The one with the green checkmark. We can finally express the binomial factors of this trinomial by writing down a pair of parentheses with an [latex]x[/latex] as the leading term.
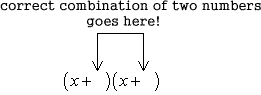
Since the correct combination of numbers is 5 and 2, our final answer should be
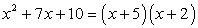
Check your answer using the FOIL Method to verify if the product of the two binomials gives back the original trinomial.
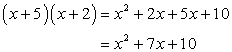
Example 2: Factor the trinomial [latex]x^2-2x-15[/latex] as a product of two binomials.
The coefficient of the squared term is 1 so this must be the “easy” case. Now, we need to find two numbers that when multiplied would result to the last constant ([latex]c=-15[/latex]), and when added give the middle constant ([latex]b=-2[/latex]).
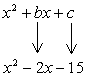
Since the product must be negative (value of [latex]c[/latex]), the pair of numbers should have opposite signs, i.e. one number is positive while the other is negative. In addition, since the sum of two numbers is negative (value of [latex]b[/latex]), the negative number must have a larger absolute value than the positive number.
Possible combinations of numbers by trial and error are listed in the following table.

The fourth option in the table satisfies the requirements. So, the binomial factors of this trinomial are
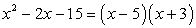
Example 3: Factor the trinomial [latex]x^2+5x-24[/latex] as a product of two binomials.
For this example, the pair of numbers must get [latex]c=-24[/latex] when multiplied and must add up to [latex]b=5[/latex]. This means that the two numbers are opposite in signs, and the positive number has a larger absolute value as compared to the negative number.
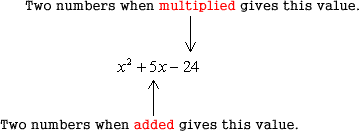
Here is the list of possible combinations:
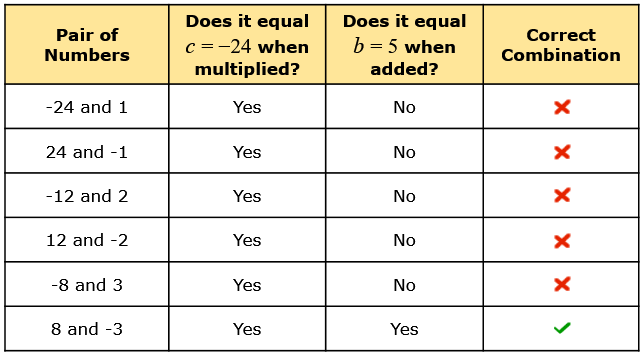
Since the pair of 8 and –3 satisfies the conditions, our factored trinomial looks like this.
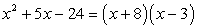
Example 4: Factor the trinomial [latex]x^2-9x+14[/latex] as a product of two binomials.
In this case, the two numbers must have a product of [latex]c=14[/latex] and a sum of [latex]b=-9[/latex]. This means that the numbers must have the same sign, either both positive or both negative. However, since the sum of the two numbers is negative, we can say that the pair should be both negative as well.
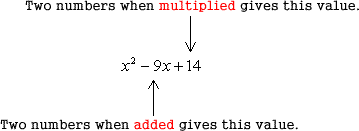
By trial and error, the possible combinations are

Since the pair of –7 and –2 satisfies the conditions, therefore our factored trinomial looks like this.
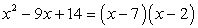
Example 5: Factor the trinomial [latex]x^2+13x+12[/latex] as a product of two binomials.
Solution:
I need to find two numbers such that their product (when multiplied) equals 12, and their sum (when added) equals 13.
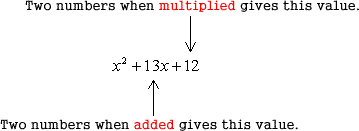
The correct combination should be 12 and 1. Why?
It is because the product and the sum are 12 and 13, respectively, which match the coefficients of the trinomial above perfectly.
- Product: [latex](12)(1)=12[/latex]
- Sum: [latex]12+1=13[/latex]
The final answer is
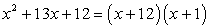
Example 6: Factor the trinomial [latex]x^2+8x-20[/latex] as a product of two binomials.
Solution:
I need to get a product of [latex]c=-20[/latex] and a sum of [latex]b=8[/latex]. Since the product is negative, the two numbers must have different signs.
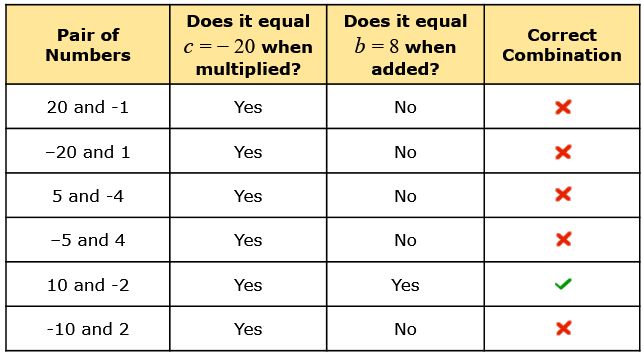
Since the pair of numbers 10 and –2 satisfies the given conditions, our final answer is
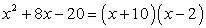
Example 7: Factor the trinomial [latex]x^2-x-42[/latex] as a product of two binomials.
Solution:
I need to get a product of [latex]c=-24[/latex] and a sum of [latex]b=-1[/latex]. Since the product is negative, the two numbers must have different signs.
Here is the list of possible combinations of numbers.
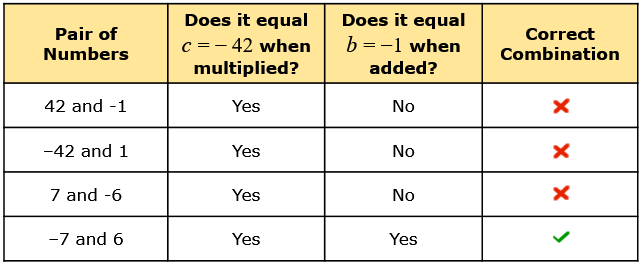
Since the pair of numbers –7 and 6 satisfies the given conditions, our final answer is
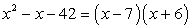
Example 8: Factor the trinomial [latex]x^2-10x+21[/latex] as a product of two binomials.
Solution:
I need to get a product of [latex]c=21[/latex] and a sum of [latex]b=-10[/latex]. Since the product is positive, the two numbers must have the same sign, either both positive or negative.
Here is the list of possible combinations of numbers.

Since the pair of numbers –7 and –3 satisfies the given conditions (product and sum), our final answer is
[latex]\large{x^2-10x+21=(x-7)(x-3)}[/latex]
Example 9: Factor the trinomial [latex]-x^2+4x-4[/latex] as a product of two binomials.
Solution:
The first thing that stands out is that the coefficient of [latex]x^2[/latex] term is not equal to [latex]1[/latex]. In fact, we have [latex]a=-1[/latex]. First, we need to factor that [latex]-1[/latex] out of the trinomial. By doing so, the signs of each term of the trinomial will switch.
- Factoring out [latex]-1[/latex] from [latex]-x^2+4x-4[/latex]
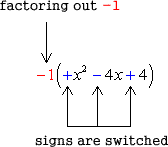
- Next, let’s focus our attention to the trinomial inside the parenthesis. At this point, it should be clear what to do since the coefficient of the [latex]x^2[/latex] is equal to [latex]1[/latex].
We need to find two numbers such that their product is [latex]c=4[/latex] and their sum is [latex]b=-4[/latex].
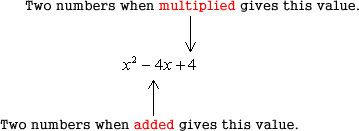
This is the list of possible combinations.

Since the pair of numbers –2 and –2 satisfies the given conditions, the factors would be
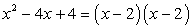
But don’t forget the -1 that was factored out in the beginning! We need to incorporate that into our final answer which is
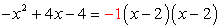
You may also be interested in these related math lessons or tutorials:
Factoring Trinomial where a>1
Factoring Trinomial using “Box” Method
