Cramer’s Rule for a 2×2 System (with Two Variables)

Cramer’s Rule is another method that can solve systems of linear equations using determinants.

In terms of notations, a matrix is an array of numbers enclosed by square brackets while a determinant is an array of numbers enclosed by two vertical bars.

Notations

square brackets indicate a matrix, for example [a,b;c,d]

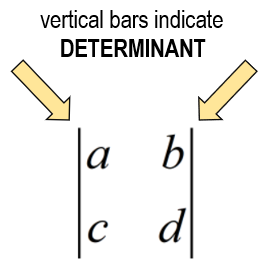
vertical bars (also known as "pipes") indicate a determinant of a matrix, for example, | a,b ; c,d |

The formula to find the determinant of a 2 x 2 matrix is very straightforward.

Let’s have a quick review:

The Determinant of a 2 x 2 Matrix

Let matrix A has entries a and b on the first row, and c and d on the second row which can be expressed as A = [a,b;c,d]. Then, the determinant of matrix A is |A| = determinant of [a,b;c,d] = |a,b;c,d| = a*d-b*c.

Quick Examples of How to Find the Determinants of a 2 x 2 Matrix

Example 1: Find the determinant of the matrix [latex]A[/latex] below.

Matrix A is a 2x2 square matrix with elements 1 and 2 on its first row, and elements 3 and 4 on its second row. Alternatively, we can write matrix A as A = [1,2;3,4].

The determinant of matrix A which can be written as det [1,2;3,4] = |A| = |1,2;3,4| = (1)(4) - (2)(3) = 4-6 = -2. Therefore, the determinant of matrix A is negative 2.

Example 2: Find the determinant of the matrix [latex]B[/latex] below.

Matrix B is a 2 by 2 square matrix with entries 5 and -1 on the first row, and entries 2 and -3 on the second row. This matrix can be expressed as B=[5,-1;2,-3].

The determinant of matrix B which can be written as det [5,-1;2,-3] = |B| = |5,-1;2,-3| = (5)(-3) - (-1)(2) = -15-(-2) = -15 + 2 = -13. That makes the determinant of matrix B as negative 13.

Example 3: Find the determinant of the matrix [latex]C[/latex] below.

Matrix C is a square matrix having two rows and two columns. The elements on the first row are -1 and 3 while the elements on the second row are -7 and -9. Thus, matrix C = [-1,3;-7,-9].

The determinant of matrix C which can be written as det [-1,3;-7,-9] = |C| = |-1,3;-7,-9| = (-1)(-9) - (3)(-7) = 9+21 = -15 + 2 = 30. Thus, the determinant of matrix C is positive 30.

After knowing how to find the determinant of a 2 x 2 matrix, you’re now ready to learn the procedures or steps on how to use Cramer’s Rule. Here we go!

Cramer’s Rules for Systems of Linear Equations with Two Variables

Given a linear system

This is a diagram showing a system of linear equations where the first linear equation is a1x+b1y=c1 while the second is a2x+b2y=c2. The x-cloumn (also known as the first column) includes the constants attached to the variable x, the y-column (also known as the second column) includes the constants attached to the y variable, and finally the constant column (also known as the third column) includes just the constants , that is, just constants without any variables attached to them.

Assign names for each matrix

coefficient matrix:

X – matrix:

Y – matrix:

To solve for the variable x:

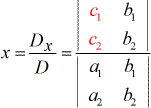
To solve for x, the formula is, x = Dx/D = (determinant of x-matrix) divided by (determinant of coefficient matrix) = |c1,b1;c2,b2| / |a1,b1;a2,b2|.

To solve for the variable y:

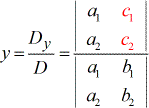
To solve for y, the formula is, y = Dy/D = (determinant of y-matrix) divided by (determinant of coefficient matrix) = |a1,c1;a2,c2| / |a1,b1;a2,b2|.

Few points to consider when looking at the formula:

1) The columns of [latex]\large{x}[/latex], [latex]\large{y}[/latex], and the constant terms [latex]\large{c}[/latex] are obtained as follows:

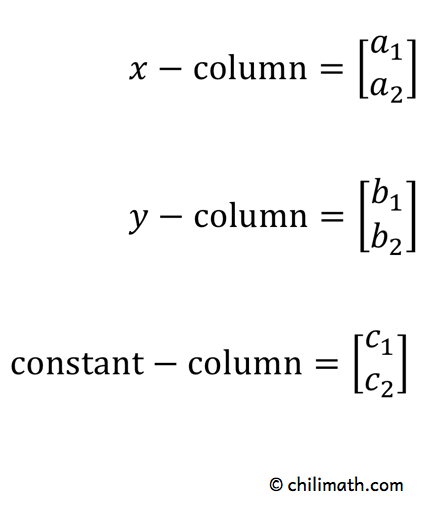
2x1 matrices of columns x, y and constant

2) Both denominators in solving [latex]\large{x}[/latex] and [latex]\large{y}[/latex] are the same. They come from the columns of [latex]\large{x}[/latex] and [latex]\large{y}[/latex].

3) Looking at the numerator in solving for [latex]\large{x}[/latex], the coefficients of [latex]\large{x}[/latex]-column are replaced by the constant column (in red).

4) In the same manner, to solve for [latex]\large{y}[/latex], the coefficients of [latex]\large{y}[/latex]-column are replaced by the constant column (in red).

Examples of How to Solve Systems of Linear Equations with Two Variables using Cramer’s Rule

Example 1: Solve the system with two variables by Cramer’s Rule

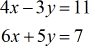
the systems of equations with two variables are 4x-3y=11 and 6x+5y=7

Start by extracting the three relevant matrices: coefficient, [latex]\large{x}[/latex], and [latex]\large{y}[/latex]. Then solve each corresponding determinant.

For coefficient matrix

Solve for the determinant of the coefficient matrix D with elements 4 and -3 on the first row, and elements 6 and 5 on the second row. The determinant of matrix D = [4,-3;6,5] = |D| = |4,-3;6,5| = (4)(5) - (-3)(6) = 20 - (-18) = 20 + 18 = 38.

For X – matrix

Solve for the determinant of the x-matrix D subscript x with elements 11 and -3 on the first row, and elements 7 and 5 on the second row. The determinant of matrix Dx = [11,-3;7,5] = |Dx| = |11,-3;7,5| = (11)(5) - (-3)(7) = 55 - (-21) = 55 + 21 = 76.

For Y – matrix

Solve for the determinant of the y-matrix D subscript y with elements 4 and 11 on the first row, and elements 6 and 7 on the second row. The determinant of matrix Dy = [4,11;6,7] = |Dx| = |4,11;6,7| = (4)(7) - (11)(6) = 28 - (66) = -38.

Once all three determinants are calculated, it’s time to solve for the values of [latex]\large{x}[/latex] and [latex]\large{y}[/latex] using the formula above.

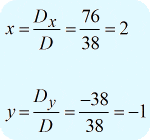
To solve for x, we have x = Dx/D = 76/38 = 2, and for y, we have y = Dy/D = -38/38 = -1.

I can write the final answer as [latex]\large{\left( {x,y} \right) = \left( {2, – 1} \right)}[/latex].

Example 2: Solve the system with two variables by Cramer’s Rule

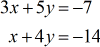
the systems of equations with two variables (namely, x and y) are 3x+5y=-7 and x+4y=-14

Setup your coefficient, [latex]\large{x}[/latex], and [latex]\large{y}[/latex] matrices from the given system of linear equations. Then calculate their determinants accordingly.

Remember that we always subtract the products of the diagonal entries.

For the coefficient matrix (use the coefficients of both [latex]x[/latex] and [latex]y[/latex] variables)

Solve the determinant of the coefficient matrix D with entries 3 and 5 on the first row, and entries 1 and 4 on the second row. The determinant of matrix D = [3,5;1,4] = |D| = |3,5;1,4| = (3)(4) - (5)(1) = 12 - (5) = 12 - 5 = 7.

For the X – matrix (replace the x-column by the constant column)

Solve the determinant of x-matrix, also known as D subscript x, with entries -7 and 5 on the first row, and entries -14 and 4 on the second row. The determinant of matrix Dx = [-7,5;-14,4] = |D| = |-7,5;-14,4| = (-7)(4) - (5)(-14) = -28 - (-70) = -28 + 70 = 42.

For the Y – matrix (replace the y-column by the constant column)

Solve the determinant of y-matrix, also known as D subscript y, with entries 3 and -7 on the first row, and entries 1 and -14 on the second row. The determinant of matrix Dy = [3,-7;1,-14] = |D| = |3,-7;1,-14| = (3)(-14) - (-7)(1) = -42 - (-7) = -42 + 7 = -35.

I hope you’re getting comfortable computing for the determinant of a 2-dimensional matrix. To finally solve the required variables, I get the following results.

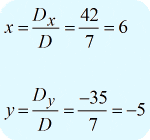
To solve for x, we divide the determinant of the x-matrix by the determinant of coefficient matrix. In the same manner, to solve for y, we divide the determinant of the y-matrix by the determinant of the coefficient matrix. Therefore, x = Dx/D = 42/7 = 6; y = Dy/D = -35/7 = -5. So the final answer is (x,y) = (6,-5).

Writing the final answer in point notation, I got [latex]\large{\left( {x,y} \right) = \left( {6, – 5} \right)}[/latex].

Example 3: Solve the system with two variables by Cramer’s Rule

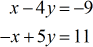
This problem can actually be solved quite easily by the Elimination Method. This is because the coefficients of variable x are the “same” but only opposite in signs ( +1 and −1 ). To solve this using the elimination method, you add their corresponding columns and the x-variable goes away – leaving you with a one-step equation in [latex]\large{y}[/latex]. I am mentioning this because every technique has shortcomings and it is best to pick the most efficient. Always get clarification from your teacher if it is okay to use another approach when the method is not specified on a given problem.

Anyway, since we are learning how to solve by Cramer’s Rule, let’s go ahead and work it out with this method.

I will construct three matrices ( coefficient, [latex]\large{x}[/latex] and [latex]\large{y}[/latex]) and evaluate their corresponding determinants.

For coefficient matrix

For the coefficient matrix D = [1,-4;-1,5], its determinant is solved as follows: |D| = |1,-4;-1,5| = (1)(5) - (-4)(-1) = 5 - (4) = 1. Thus, |D| = 1.

For X – matrix ( written as uppercase D with subscript x )

For the x-matrix Dx = [-9,-4;11,5], its determinant is solved as follows: |Dx| = |-9,-4;11,5| = (-9)(5) - (-4)(11) = -45 - (-44) = -45 + 44 = -1. Thus, |Dx| = -1.

For Y – matrix (written as uppercase D with subscript y)

For the y-matrix Dy = [1,-9;-1,11], its determinant is solved as follows: |Dy| = |1,-9;-1,11| = (1)(11) - (-9)(-1) = 11 - (9) = 11 - 9 = 2. Thus, |Dy| = 2.

After obtaining the values of the three required determinants, I will calculate [latex]\large{x}[/latex] and [latex]\large{y}[/latex] as follows.

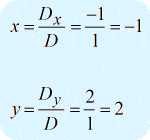
Solving for the value of x, divide the determinant of the x-matrix by the determinant of coefficient matrix. Similarly, to solve for y, divide the determinant of the y-matrix by the determinant of the coefficient matrix. Thus, x = Dx/D = -1/1 = -1; y = Dy/D = 2/1 = 2. So the final answer is (x,y) = (-1,2).

The final answer in the point form is [latex]\large{\left( {x,y} \right) = \left( { – 1,2} \right)}[/latex] .

Example 4: Solve by Cramer’s Rule the system with two variables

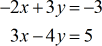
the system of linear equations with two variables are -2x+3y=-3 and 3x-4y=5

Since we have gone over a few examples already, I suggest that you try this problem on your own. Then, compare your answers to the solution below.

If you get it right the first time that means you’re becoming a “pro” with regards to Cramer’s Rule. If you didn’t, try to figure out what went wrong and learn to not commit the same error next time. This is how you become better at math. Study many kinds of problems and more importantly, do a lot of independent practice.

For coefficient matrix

Solve for the coefficient matrix D, we have D = [-2,3;3,-4], the steps to solve its determinant is |D| = |-2,3;3,-4| = (-2)(-4) - (3)(3) = 8 - (9) = -1. And so, |D| = -1.

For X – matrix

Solve for the x-matrix Dx, we have Dx= [-3,3;5,-4], the steps to solve its determinant is |Dx| = |-3,3;5,-4| = (-3)(-4) - (3)(5) = 12 - (15) = -3. And so, |Dx| = -3.

For Y – matrix

Solve for the y-matrix Dy, we have Dy = [-2,-3;3,5], the steps to solve its determinant is |Dy| = |-2,-3;3,5| = (-2)(5) - (-3)(3) = -10 - (-9) = -10 + 9 = -1. That makes, |Dy| = -1.

You should get the answer below…

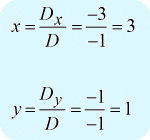
To solve for the x, we have x = Dx/D = -3/-1 = 3. Therefore, x equals 3. Next, to solve for y, we show that y = Dy/D = -1/-1 =1. Therefore, y equals 1.

Example 5: Solve the system with two variables by Cramer’s Rule

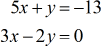
the systems of linear equations to solve are the following: 5x+y=-13, 3x-2y=0

For our last example, I included a zero in the constant column. Every time you see the number zero in the constant column, I highly recommend using Cramer’s Rule to solve the system of linear equations. Why? Because the calculation of the determinants for [latex]\large{x}[/latex] and [latex]\large{y}[/latex] matrices drastically become super easy. Check it out yourself!

For coefficient matrix

The determinant of the coefficient D = [5,1;3,-2] is solved as |D| = |5,1;3,-2| = (5)(-2) - (1)(3) = -13.

For X – matrix

The determinant of the x-matrix Dx = [-13,1;0,-2] is solved as |Dx| = |-13,1;0,-2| = (-13)(-2) - (1)(0) = 26.

For Y – matrix

The determinant of the y-matrix Dy = [5,-13;3,0] is solved as |Dy| = |5,-13;3,0| = (5)(0) - (-13)(3) = 0 + 39 = 39.

The final solution to this problem is

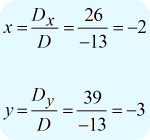
To solve x, we divide x-matrix by coefficient matrix which gives us x = Dx/D = 26/-13 = -2. To solve y, we divide y-matrix by coefficient matrix which gives us y = Dy/D = 39/-13 = -3.

You might also be interested in:

Cramer’s Rule 3×3