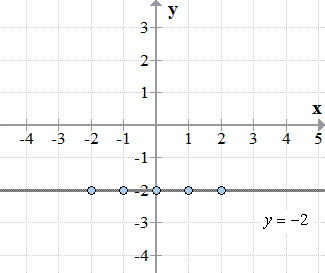How to Graph Vertical and Horizontal Lines

The equation of a vertical line comes in the form

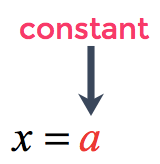
x=a where a is a constant

where [latex]a[/latex] is just a constant

Notice that this equation doesn’t contain any variable [latex]y[/latex]. The absence of [latex]y[/latex] means that it can take any values. Here’s an example.

An Example of Graphing a Vertical Line

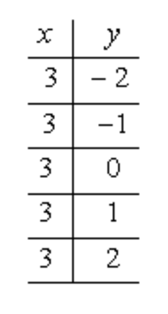
Graph the vertical line [latex]x = 3[/latex].

The equation doesn’t have the variable [latex]y[/latex] which implies that it could assume any numerical values for [latex]y[/latex]. In the table of values, you will see that “[latex]3[/latex]” is the repeating value in the column of [latex]x[/latex] while having different values in the column of [latex]y[/latex].

This is precisely the interpretation of the equation [latex]x = 3[/latex].

a table with x values of 3, 3, 3, 3, 3 and y values of -2, -1, 0, 1, 2.

So, we can now plot the points on the [latex]xy[/latex]–axis to see how it looks. As you can see, it is a vertical line parallel to the [latex]y[/latex]-axis and passing through the point [latex]\left( {3,0} \right)[/latex].

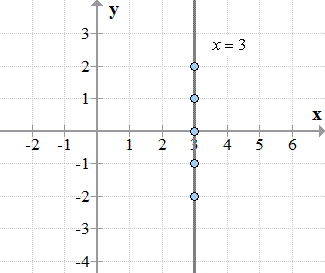
a vertical line on the xy axis with plotted points (3,-2), (3,-1), (3,0), (3,1) and (3,2)

On the other hand, the equation of a horizontal line comes in the form

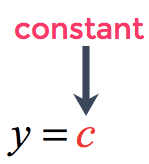
y=c where c is a constant

where [latex]c[/latex] is just a constant

This time around, the equation doesn’t have any variable [latex]x[/latex]. The absence of [latex]x[/latex] means that the variable [latex]x[/latex] can take any numerical values while the value of [latex]y[/latex] is being held constant. Here’s an example.

An Example of Graphing a Horizontal Line

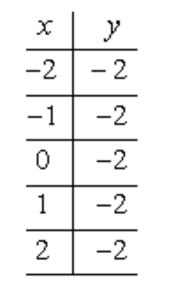
Graph the horizontal line [latex]y = – 2[/latex].

Since we have no [latex]x[/latex]-variable in the equation, it is okay to pair the [latex]y[/latex]-coordinate of [latex] – 2[/latex] with any [latex]x[/latex]-values. When you construct the table of values for this, the [latex]y[/latex]-coordinates will be the same throughout while the [latex]x[/latex]-coordinates can have different values.

Observe, the [latex]y[/latex]-column is populated with the same value of [latex] – 2[/latex].

a table of values with x values of -2, -1, 0, 1, 2 while with y values of -2, -2, -2, -2, -2.

Graphing these points in the [latex]xy[/latex]-axis, we have a horizontal line parallel to the [latex]x[/latex]-axis and passing through the point [latex]\left( {0, – 2} \right)[/latex].

a horizontal line plotted on the xy axis passing through the points (-2,2), (-1,-2), (0,-2), (1,-2), and (2,-2)