Multiplying Rational Expressions
Rational expressions are multiplied the same way as you would multiply regular fractions. Nothing more, nothing less. As you may have learned already, we multiply simple fractions using the steps below.
Review the Steps in Multiplying Fractions
- Multiply the numerators.
- Multiply the denominators
- Simplify the “new” fraction by canceling common factors. Most of the time, you will need to expand a number as a product of its factors to identify common factors in the numerator and denominator which can be canceled. What you are doing really is reducing the fraction to its simplest form. A fraction is in simplest form if the Greatest Common Divisor is [latex]\color{red}+1[/latex].
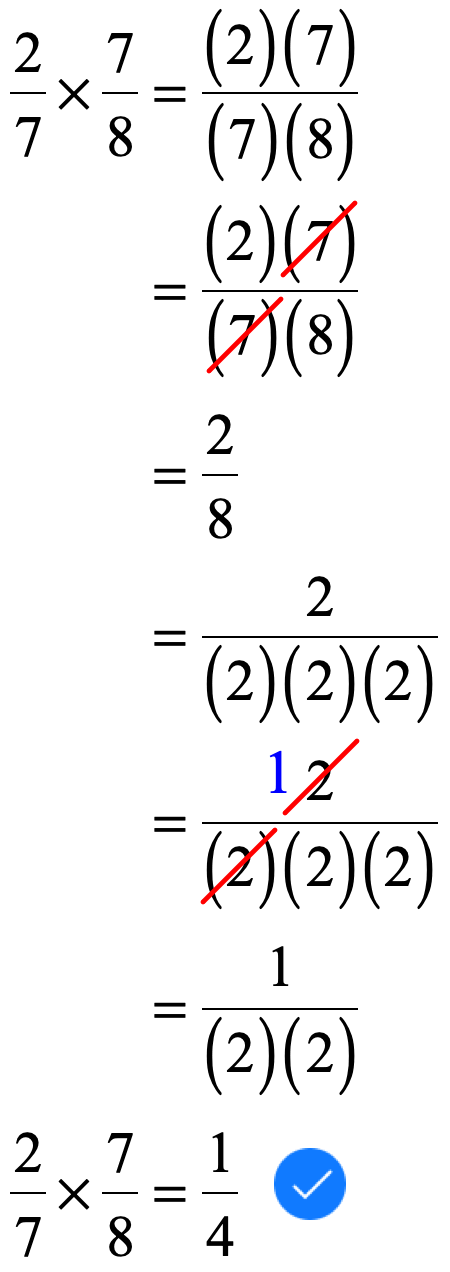
Therefore, when you multiply rational expressions, apply what you know as if you are multiplying fractions.
The best way how to learn how to multiply rational expressions is to do it. That’s why we are going to go over five (5) worked examples in this lesson.
Examples of How to Multiply Rational Expressions
Example 1: Multiply the rational expressions below.
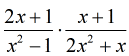
I see that both denominators are factorable. The first denominator is a case of the difference of two squares. The second denominator is easy because I can pull out a factor of [latex]x[/latex].
This is how it looks.
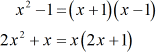
- Factor out the denominators.
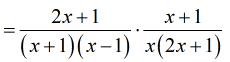
- Now, I can multiply across the numerators and across the denominators by placing them side by side.
At this point, I compare the top and bottom factors and decide which ones can be crossed out.
![[(2x+1)(x+1)] divided by [(x+1)(x-1)(x)(2x+1)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex1_steps_r3_c2.gif)
- By color-coding the common factors, it is clear which ones to eliminate.
Both factors [latex]2x + 1[/latex] and [latex]x + 1[/latex] can be canceled out as shown below.
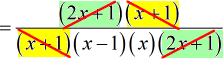
- What remains on top is just the number [latex]1[/latex].
And so we have this as our final answer.
Try not to distribute it back and keep it in factored form. However, if your teacher wants the final answer to be distributed, then do so. Either case should be correct. It’s just a matter of preference.
![1/[x(x-1)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex1_steps_r4_c2.gif)
Example 2: Multiply the rational expressions below.
![[(x^2+7x+10)/(x^2-9x+14)] × [(x^2-9x+14)/(x^2+6x+5)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex2_steps_r1_c1.gif)
We need to factor out all the trinomials. The good news is that this type of trinomial, where the coefficient of the squared term is [latex]+1[/latex], is very easy to handle. In fact, I called this trinomial wherein the coefficient of the quadratic term is [latex]+1[/latex] the easy case.
Below is the link to my separate lesson that discusses how to factor a trinomial of the form [latex]{\color{red} + 1}{x^2} + bx + c[/latex].
Factoring Trinomial – Easy Case
Let’s factor out the numerators and denominators of the two rational expressions.
➤ Factoring out the numerators:
Starting with the first numerator, find two numbers where their product gives the last term, [latex]10[/latex], and their sum gives the middle coefficient, [latex]7[/latex]. I’m thinking of [latex]+5[/latex] and [latex]+2[/latex]. They are the correct numbers but I will it to you to verify.
For the second numerator, the two numbers must be [latex]−7[/latex] and [latex]+1[/latex] since their product is the last term, [latex]-7[/latex], while the sum is the middle coefficient, [latex]-6[/latex].
➤ Factoring out the denominators
To factor out the first denominator, find two numbers with a product of the last term, [latex]14[/latex], and a sum of the middle coefficient, [latex]-9[/latex]. By trial and error, the numbers are [latex]−2[/latex] and [latex]−7[/latex]. However, you should always verify it.
Now for the second denominator, think of two numbers such that when multiplied gives the last term, [latex]5[/latex], and when added gives [latex]6[/latex]. Obviously, they are [latex]+5[/latex] and [latex]+1[/latex].
The correct factors of the four trinomials are shown below.
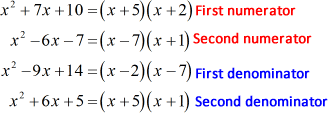
- Factorize the numerators and denominators completely.
![= {[(x+5)(x+2)]/[(x-2)(x-7)]} times {[(x-7)(x+1)]/[(x+5)(x+1)]}](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex2_steps_r1_c2.gif)
- Multiply them together – numerator times numerator, and denominator times denominator.
That means we place them side-by-side so that they become a single fraction with one fractional bar.
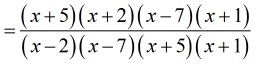
- The color schemes should aid in identifying common factors that we can get rid of.
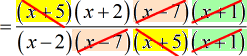
- Yep! We cleaned it out beautifully. This is our final answer.
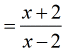
Example 3: Multiply the rational expressions below.
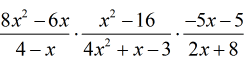
In this problem, there are six terms that need factoring. However, most of them are easy to handle and I will provide suggestions on how to factor each.
But, I want to show a quick side-calculation on how to factor out the trinomial [latex]\color{red}4{x^2} + x – 3[/latex] because it can be challenging to some.


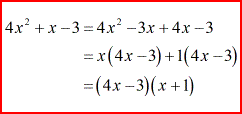
- Factoring out all the terms.
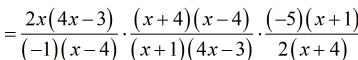
- Multiply all of them at once by placing them side by side. All numerators stay on top and denominators at the bottom.
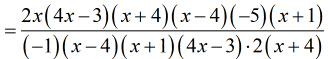
- I decide to cancel common factors one or two at a time so that I can keep track of them accordingly. Otherwise, I may commit “careless” errors.
I will first get rid of the two binomials [latex]4x – 3[/latex] and [latex]x – 4[/latex].
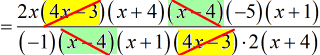
- Simplify.
![=[(2x)(x+4)(-5)(x+1)]/[(-1)(x+1)(2)(x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex3_steps_r4_c2.gif)
- Next, I will eliminate the factors [latex]x + 4[/latex] and [latex]x + 1[/latex].
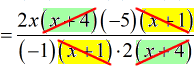
- Cancel out the [latex]2[/latex] found in the numerator and denominator.
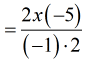
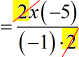
- At this point, there’s really nothing else to cancel. However, there’s something I can simplify by division.
Notice that [latex]\left( { – 5} \right) \div \left( { – 1} \right) = 5[/latex].
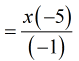
- There you go! This is our final answer.
Example 4: Multiply the rational expressions below.
![{[(x^5)/(4x^3-3x^2)]}[(4x^2+5x-6)/(x^2-2x-35)][(x^2+10x+25)/(x^2+7x+10)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex4_steps_r1_c1.gif)
As you can see, there are so many things going on in this problem. However, don’t be intimidated by how it looks. Start by factoring each term completely. The problem will become easier as you go along.
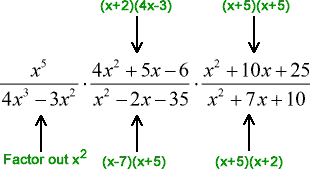
In fact, once we have factored out the terms correctly, the rest of the steps become manageable.
- Factor out each term completely.
![= [x^5/x^2(4x-3)]{[(x+2)(4x-3)]/[(x-7)(x+5)]}{[(x+5)(x+5)]/[(x+5)(x+2)]}](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex4_steps_r1_c2.gif)
- Multiply by placing them in a single fractional symbol. All numerators are written side by side on top while the denominators are at the bottom.
![= [x^5 (x+2)(4x-3)(x+5)(x+5)]/[x^2(4x-3)(x-7)(x+5)(x+5)(x+2)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex4_steps_r3_c2.gif)
- I will first cancel all the [latex]x + 5[/latex] terms.
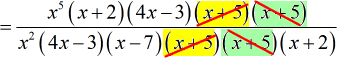
- Simplify.
![= [x^5(x+2)(4x-3)]/[x^2(4x-3)(x-7)(x+2)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex4_steps_r4_c2.gif)
- Next, cross out the [latex]x + 2[/latex] and [latex]4x – 3[/latex] terms.
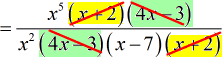
- At this point, I can also simplify the monomials with variable [latex]x[/latex].
![= x^5/[x^2(x-7)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex4_steps_r5_c2.gif)
- There are five [latex]\color{red}x[/latex] on top and two [latex]\color{blue}x[/latex] at the bottom.
Canceling the [latex]x[/latex] with one-to-one correspondence should leave us three [latex]x[/latex] in the numerator.
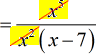
- This is the final answer.
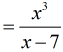
Caution: Don’t do this!
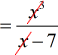
Note that the [latex]x[/latex] in the denominator is not by itself. It is part of the entire term [latex]x−7[/latex]. This is a common error by many students. Don’t fall into this common mistake.
Example 5: Multiply the rational expressions below.
![[(-3x^2+27)/(x^3-1)][(7x^3+7x^2+7x)/(x^2-3x)][(x-1)/21]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex5_steps_r1_c1.gif)
I am sure that by now, you are getting better on how to factor. The only thing I need to point out is the denominator of the first rational expression, [latex]{x^3} – 1[/latex]. This is a special case called the difference of two cubes.
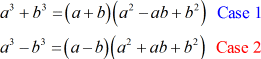
In this problem, I will use Case 2 because of the “minus” symbol between [latex]a^3[/latex] and [latex]b^3[/latex]. Hence, it is a case of the difference of two cubes.
Case 1 is known as the sum of two cubes because of the “plus” symbol.
Below are the factors.
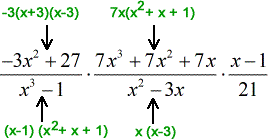
- Factorize all the terms as much as possible.
![= {[(-3)(x+3)(x-3)]/[(x-1)(x^2+x+1)]}{[7x(x^2+x+1)]/[x(x-3)]}[(x-1)/21]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex5_steps_r1_c2.gif)
- Multiply the numerators together and do the same with the denominators.
}/{(x-1)(x^2+x+1)[x(x-3)](21)}](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex5_steps_r3_c2.gif)
- I will first get rid of the trinomial [latex]{x^2} + x + 1[/latex].
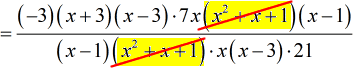
- Next, I will cancel the terms [latex]x – 1[/latex] and [latex]x – 3[/latex] because they have common factors in the numerator and the denominator.
![={(-3)(x+3)(x-3)[7x(x-1)]}/{(x-1)[x(x-3)](21)}](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex5_steps_r4_c2.gif)
- Here it goes. I hope the color-coding helps you keep track of which terms are being canceled out.
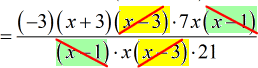
- I see a single [latex]x[/latex] term on both the top and bottom.
![= [(-3)(x+3)(7x)]/[(x)(21)]](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex5_steps_r5_c2.gif)
- Cross out that [latex]x[/latex] as well.
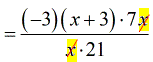
- At this point, I will multiply the constants on the numerator.
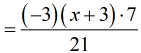
- Since [latex]\left( { – 3} \right)\left( 7 \right) = – 21[/latex],
![=[(-21)(x+3)]/21](https://www.chilimath.com/wp-content/uploads/2017/07/multi_ex5_steps_r7_c2.gif)
- We can cancel the common factor [latex]21[/latex] but leave [latex]-1[/latex] on top.
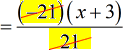
- I can keep this as the final answer. However, it will look better if I distribute [latex]-1[/latex] into [latex]x+3[/latex].
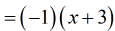
- We got it again!
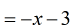
You may also be interested in these related math lessons or tutorials:
