Matrix Scalar Multiplication: Product of a Scalar and a Matrix

Matrix multiplication usually falls into one of two types or classifications. The first one is called Scalar Multiplication, also known as the “Easy Type“; where you simply multiply a number into each and every entry of a given matrix.

The second one is called Matrix Multiplication which is discussed in a separate lesson.

In this lesson, we will focus on the “Easy Type” because the approach is extremely simple or straightforward.

“Formula” of Scalar Multiplication (Easy Type)

Scalar "c" is being multiplied to each entry or element of Matix A. The scalar value"c" is multiplied to Matrix A. The result equals to matrix cA with elements c*a1, c*a2, and c*a3 on the first row, elements c*a4, c*a5 and c*a6 on the second row, and elements a*a7, a*a8, and c*a9 on the third row. This can also be written as c*A=[c*a1,c*a2,c*a3;c*a4,c*a5,c*a6;c*a7,c*a8,c*a9].

Here’s the simple procedure as shown by the formula above.

Take the number outside the matrix (known as the scalar) and multiply it by each and every entry or element of the matrix.

Examples of Scalar Multiplication

Directions: Given the following matrices, perform the indicated operation. Apply scalar multiplication as part of the overall simplification process.

Matrix A has entries of -5,2, and 0 on the first row; entries of 7,-2 and 0 on the second row; and entries of -1,3 and 2 on the third row. Matrix A =[-5,2,0;7,-3,4;-1,3,2].
Matrix B has entries of 8,1, and 2 on the first row; entries of -5,6 and 7 on the second row. Matrix B =[8,1,2;-5,6,7].
Matrix C has entries of 0,-1, and 8 on the first row; entries of 6,-14 and 2 on the second row; and entries of 9,5 and 1 on the third row. Matrix C =[0,-1,8;6,-14,8;9,5,1].
Matrix D has elements 6 and -2 on its first row and elements 3 and 7 on its second row. Matrix D equals = [6,-2;3,7].
Matrix E has entries -5 and 1 on the first row, entries 0 and 2 on the second row, and entries -11 and 7 on the third row. That means we can write this matrix as E = [-5,1;0,2;-11,7].
Matrix F is a 2 by 2 matrix with elements 1 and -2 on the first row, and elements -3 and 4 on the second row. Therefore, matrix F = [1,-2;-3,4].

Example 1: Perform the indicated operation for [latex]2A[/latex].

I will take the scalar 2 (similar to the coefficient of a term) and distribute it by multiplying it to each entry of matrix [latex]A[/latex]. In case you forgot, you may review the general formula above.

Since matrix [latex]A[/latex] is

Matrix A contains the elements of -5, 2 and 0 on the first row, elements 7, -3 and 4 on the second row, and elements -1, 3 and 2 on the third row. Matrix A = [-5,2,0;7,-3,4;-1,3,2].

then [latex]2A[/latex] is solved by…

The product of scalar quantity 2 and matrix A is a new matrix called 2A with elements -10, 4 and 0 on the first row, elements 14, -6 and 8 on the second row, and elements -2, 6 and 4 on the third row. We can write this as 2A = [-10,4,0;14,-6,8;-2,6,4].

That’s all there is to it. Done!

Example 2: Perform the indicated operation for [latex]-3B[/latex].

I will do the same thing similar to Example 1. No big deal! Multiply the negative scalar, [latex]−3[/latex], into each element of matrix [latex]B[/latex].

Since matrix [latex]B[/latex] is

Matrix B is a 2 by 3 matrix with entries of 8, 1 and 2 on the first row, and entries of -5, 6 and 7 on the second row. Matrix B can be expressed as B = [8,1,2;-5,6,7].

then matrix [latex]-3B[/latex] is solved by…

The product of scalar -3 and matrix B is the matrix with entries of -24, -3 and -6 on its first row, entries of 15, -18 and -21 on its second row. Therefore -3B = [-24,-3,-6;15,-18.-21].

Did you arrive at the same final answer? If not, please recheck your work to make sure that it matches the correct answer.

Example 3: Perform the indicated operation for [latex]-2D + 5F[/latex].

To solve this problem, I need to apply scalar multiplication twice and then add their results to get the final answer.

  • First, find the value of matrix [latex]-2D[/latex]

I know that matrix [latex]D[/latex] is

Matrix D is a 2 by 2 matrix (square matrix) that contains the elements 6 and -2 on the first row, and 3 and 7 on the second row. This means D = [6,-2;3,7].

Therefore, [latex]-2D[/latex] is obtained as follows using scalar multiplication.

The product of -2 and matrix D is also a 2 by 2 matrix with entries -12 and 4 on its first row, and entries -6 and -14 on its second row. We can write it as -2D = [-12,4;-6,-14].
  • Second, find the value of [latex]5F[/latex]

Matrix [latex]F[/latex] is given as

Matrix F is a 2 by 2 matrix with entries of 1 and -2 on its first row, and entries of -3 and 4 on its second row. Matrix F = [1,-2;-3,4].

That means [latex]5F[/latex] is solved using scalar multiplication.

The scalar 5 is multiplied to Matrix F. The product of the scalar quantity and the matrix is a matrix with elements 5 and -10 on the first row, and elements -15 and 20 on the second row. Therefore, 5F=[5,-10;-15,20].
  • Now, I can solve for [latex]-2D+5F[/latex] by adding the values of matrices [latex]-2D[/latex] and [latex]5F[/latex], as shown above. Check out the solution to review how to add and subtract matrices.
The sum of the product of -2 and matrix D, and five times of matrix F is a 2 by 2 matrix with entries -7 and -6 on its first row, and entries -21 and 6 on its second row. This can be compactly written as -2D + 5F = [-7,-6;-21,6].

That’s it!

Example 4: What is the difference of [latex]4A[/latex] and [latex]3C[/latex]?

At this point, you should have mastered already the skill of scalar multiplication. The very first step is to find the values of [latex]4A[/latex] and [latex]3C[/latex], respectively. Then we subtract the newly formed matrices, that is, [latex]4A-3C[/latex].

Finding the value of [latex]4A[/latex]

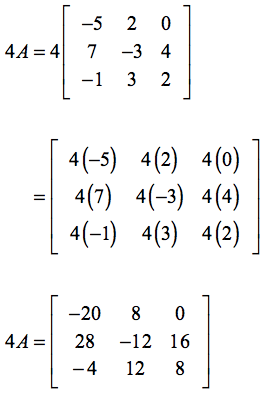
Th product of 4 and matrix A is a 3 by 3 matrix with elements -20, 8, and 0 on the first row; 28, -12, and 16 on the second row; and -4, 12, and 8 on the third row.

Finding the value of [latex]3C[/latex]

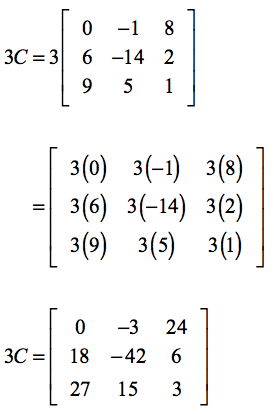
The product of 3 and C is a 3 by 3 matrix with entries 0, -3, and 24 on the first row; 18, -42 and 6 on the second row; and 27, 15, and 3 on the third row.

Finally, we subtract [latex]4A[/latex] by [latex]3C[/latex].

(4A)-3C = [-20,11,-24; 10,30,10; -31,-3, 5]

You may also be interested in these related math lessons or tutorials:

Adding and Subtracting Matrices

Matrix Multiplication